Solve the system by graphing.
x + y = 4
y = 2x + 1
 
                        (1, 3)
 
Check Answer
http://www.coursesavior.com/free/linear-equation-solver/
Explanation
 
Replace all occurrences of y “in x + y = 4” with 2x + 1
x + 2x + 1 = 4
simplify = 3x + 1 = 4
solve 3x + 1 = 4 for x
subtract 1 from both sides.
3x = 3
divide both sides by 3.
x = 1
solve y = 2x + 1 for y
we know x = 1, so we plug it in
y = 2(1) + 1 and simplify, y = 2(1) + 1 = 2 + 1
y = 3 

Solve the system by substitution.
        y = 2x - 8
        4x + 3y = 1

                                  , -3 )

Check Answer
http://www.coursesavior.com/free/linear-equation-solver/
Explanation
 
Replace all occurrences of y in 4x+3y=1 with 2x−8.
4x + 3 (2x−8) = 1
y=2x−8
Simplify the left side.10x – 24 = 1
Y = 2x − 8
Solve for x in 10x−24=1.
x =

y = 2x − 8
Replace all occurrences of x in y = 2x − 8 with
y = 2 () − 8.
Simplify 2 () − 8.
y = − 3
 

Solve the system by substitution.
y = x – 5
3x – 4(y-2) = 28 – x
 
                            (x, y) | y = x – 5
 
Replace all occurrences of y in 3x−4(y−2) = 28 − x with x − 5
3x − 4((x − 5) −2) = 28 − x
y = x − 5
Simplify the left side.
Simplify 3x − 4((x − 5) −2)
−x + 28 =28−x
y = x−5
Solve for x in −x + 28 = 28 − x.
Move all terms containing x to the left side of the equation. Add x
to both sides of the equation.
−x + 28 + x = 28
y = x−5
Combine the opposite terms in −x+28+x.
Add −x and x.
0 + 28 = 28
y = x – 5
 

Solve the system by addition method.
        3x+2y=3
        4x-3y =-13
 
            (-1, 3)
 
Check Answer
http://www.coursesavior.com/free/linear-equation-solver/
Explanation
 
Solve for x in 3 x + 2y = 3.
Subtract 2y
from both sides of the equation.
3x = 3 − 2y
4x −3y = −13
Divide each term in 3x = 3 − 2y, by 3, and simplify.
x = 1 −
4x − 3y = −13
Replace all occurrences of x in 4x − 3y = −13 with 1 −
4 (1 −) − 3y = −13
x = 1 −

Simplify the left side.
4 −= −13
x = 1 −
Solve for y in 4 - = −13.

Move all terms not containing y to the right side of the equation.
Subtract 4 from both sides of the equation.
 = − 13 − 4
x = 1 −

Subtract 4 from −13.
 = −17
x = 1 −
Multiply both sides of the equation by −.
(−) = − ⋅  −17
x = 1 −
y = 3
x = 1 −
Replace all occurrences of y with 3 in each equation.
x = −1
y = 3

Solve the system by addition method.
            3x-y=5
            -6x+2y=1
 

    NO SOLUTION EXIST
 
Check Answer
http://www.coursesavior.com/free/linear-equation-solver/
Explanation
 
Multiply each equation by the value that makes the coefficients of y opposite.
(2) ⋅ (3x − y) = (2) (5)
−6x + 2y = 1
6x − 2y = 10
−6x + 2y = 1
Add the two equations together to eliminate y from the system.
6x − 2y = 10 + −6x + 2y = 1
0 = 11
Since 0 ≠ 11, there are no solutions.
No solution exists 

Determine if the system is independent, dependent, or inconsistent.
            y = 3x - 5
            y = 3x + 2
 
    Inconsistent
 
Check Answer
http://www.coursesavior.com/free/linear-equation-solver/
Explanation
 
Eliminate the equal sides of each equation and combine.
3x – 5 = 3x + 2
Solve 3x – 5 = 3x + 2 for x.
Move all terms containing x to the left side of the equation.
Subtract 3x from both sides of the equation.
3x − 5−3x = 2
Combine the opposite terms in 3x − 5 − 3x
−5 = 2
Since −5 ≠ 2, there are no solutions.
No solution / Inconsistent
 

Determine if the system is independent, dependent, or inconsistent.
2x+2y=8
x+y=4
 
    Dependent
 
Subtract y from both sides of the equation.
x = 4 − y
2x + 2y = 8
Replace all occurrences of x with 4−y in each equation.
Replace all occurrences of x in 2x+2y=8 with 4−y
2(4−y) + 2y = 8
x = 4 − y
Simplify the left side.
8 = 8
x = 4 − y
Remove any equations from the system that are always true.
x = 4 − y
 
If x and y are two variables in an algebraic equation and every value of x is linked with any other value of y,
then 'y' value is said to be a function of x value known as an independent variable,
and 'y' value is known as a dependent variable.
 

Determine if the system is independent, dependent, or inconsistent.
y = 2x - 3
y = 5x - 14
 
    Independent
 
Eliminate the equal sides of each equation and combine.
2x – 3 = 5x − 14
Solve 2x – 3 = 5x − 14 for x.
Move all terms containing x to the left side of the equation.
−3x – 3 = −14
Move all terms not containing x to the right side of the equation.
−3x = −11
Divide each term in −3x = −11 by −3 and simplify.
x =
Substitute  for x.
y = 5 () −14
Simplify 5 () −14.
y =

The solution to the system is the complete set of ordered pairs that are valid solutions.
x= ,
 
If x and y are two variables in an algebraic equation and every value of x is linked
with any other value of y, then 'y' value is said to be a function of x value known
as an independent variable, and 'y' value is known as a dependent variable.
 

Solve the system by the method of your choice.
3x - y = 1
x + 2y = 12
 
    (2, 5)
 
Replace all occurrences of x with 12 − 2y in each equation.
36 − 7y = 1
x = 12 − 2y
Solve for y in 36 − 7y = 1.
Move all terms not containing y to the right side of the equation.
−7y = − 35
x = 12 − 2y
Divide each term in −7y = −35 by −7 and simplify.
y = 5
x = 12 − 2y
Replace all occurrences of y with 5 in each equation.
x = 2
y = 5
g

Solve the system by the method of your choice.
2x - y = -4
3x + y = -1
 
        (-1, 2)
 
Check Answer
http://www.coursesavior.com/free/linear-equation-solver/
Explanation
 
Subtract 3x
from both sides of the equation.
y = −1 − 3x
2x − y = −4
Replace all occurrences of y with −1 −3x in each equation.
Replace all occurrences of y in 2x −y = −4 with −1 −3x.
2x− (−1 −3x) = −4
y = −1 −3x
Simplify the left side5x + 1= −4
y = −1 −3x
Solve for x in 5x + 1= −4.
x = −1
y = −1 −3x
Replace all occurrences of x with −1 in each equation.
y = 2
x = −1
The solution to the system is the complete set of ordered pairs that are valid solutions.
(−1, 2)
 

Solve the system by the method of your choice.
        x + y = 0
        x - y + 2z = 6
        2x + y - z = 1
 
            (2, -2, 1)
 
Check Answer – (Needs to be set to > No. of variables: 3)
http://www.coursesavior.com/free/linear-equation-solver/
Explanation
 
Subtract y
from both sides of the equation.
x = −y
x – y + 2z = 6
2x + y −z = 1
Replace all occurrences of x with −y in each equation.
−y −z = 1
−2y + 2z = 6
x = −y
Solve for y in −y −z =1.
y = −1 − z
−2y + 2z = 6
x = −y
Replace all occurrences of y with −1 −z in each equation.
x = 1 + z
2 + 4z = 6
y= −1 −z
Solve for z in 2 + 4z = 6.
z = 1
x = 1 + z
y = −1 − z
Replace all occurrences of z with 1 in each equation.
y = −2
x = 2
z = 1
The solution to the system is the complete set of ordered pairs that are valid solutions.
(2, −2, 1)
 

Solve the system by the method of your choice.
        x + y - z = 2
        2x - y + 3z = -5
        x – 3y + z = 4
 
                    (1, -2, -3)
 
Check Answer – (Needs to be set to > No. of variables: 3)
http://www.coursesavior.com/free/linear-equation-solver/
Explanation
 
Move all terms not containing x to the right side of the equation.
x = 2 −y + z
2x – y + 3z = −5
x − 3y + z = 4
Replace all occurrences of x with 2−y+z in each equation.
2 − 4y + 2z = 4
4 − 3y + 5z = −5
x = 2 −y + z
Solve for y in 2 −4y + 2z = 4.
− +  

4 −3y + 5z= −5
x = 2 −y + z
Replace all occurrences of y with − 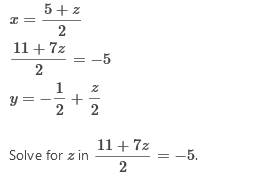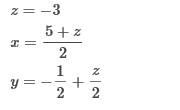+  in each equation.

Replace all occurrences of z with −3 in each equation.
y = −2
x = 1
z = −3
 

Solve the system by the method of your choice.
         x - y - z = 1
        -x - y + 2z = -2
        -x – 3y + z = -5
 
        (3, 1, 1)
 
Check Answer – (Needs to be set to > No. of variables: 3)
http://www.coursesavior.com/free/linear-equation-solver/
Explanation
 
Move all terms not containing x to the right side of the equation.
x = 1 + y + z
−x – y + 2z = −2
−x −3y + z= −5
Replace all occurrences of x with 1 + y + z in each equation
1−4y=−5
−1 −2y + z = −2
x = 1 + y + z
Solve for y in −1 −4y =−5.
y = 1
−1 −2y + z= −2
x = 1 + y + z
Replace all occurrences of y with 1 in each equation.
x = 2 + z
−3 + z = −2
y = 1
Move all terms not containing z to the right side of the equation.
z = 1
x = 2 + z
y = 1
Replace all occurrences of z with 1 in each equation.
x = 3
z = 1
y = 1
The solution to the system is the complete set of ordered pairs that are valid solutions.
(3,1,1)
 

Write a system of equations in two or three variables.
Use the method of your choice to solve the system.
One night the manager of the Sea Breeze Motel rented 5 singles and 12 doubles for a total of $1583.
The next night He rented 9 singles and 10 doubles for a total of $1701.
What is the rental charge for each type of room?
 
            Single - $79
            Double - $99
 

Write a system of equations in two or three variables.
Use the method of your choice to solve the system.
Jill, Karen, and Betsy studied a total of 93 hours last week.
Jill's and Karen's study time totaled only one-half as much as Betsy's.
If Jill studied 3 hours more than Karen, then
how many hours did each one of the girls spend studying?
 
            Karen - 14 hrs.
            Jill - 17 hrs.
            Betsy - 62 hrs.
 
Let x represent Karen's study time.  then Jills would be (x + 3) and
Betsy's would be 2[x + (x + 3)]
Question states
x + (x + 3) + 2[x + (x + 3)] = 93
solving for x
x + (x + 3) + 2x + 2x +6 = 93
6x + 9 = 93
6x = 84
84 / 6 = 14
Karen's study time x = 14 hrs.
Jill's hrs. 14 + 3 = 17
Betsy's hrs. 14 + 17 · 2 - 62