Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel

Suppose you bought a bond with an annual coupon rate of 8.2 percent one year ago for $905.
The bond sells for $942 today.

a. Assuming a $1,000 face value, what was your total dollar return on this investment over the past year?
(Do not round intermediate calculations and round your answer to the nearest whole number, e.g., 32.)
 
b. What was your total nominal rate of return on this investment over the past year?
(Do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.)
  
c. If the inflation rate last year was 4.2 percent, what was your total real rate of return on this investment?
(Do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.)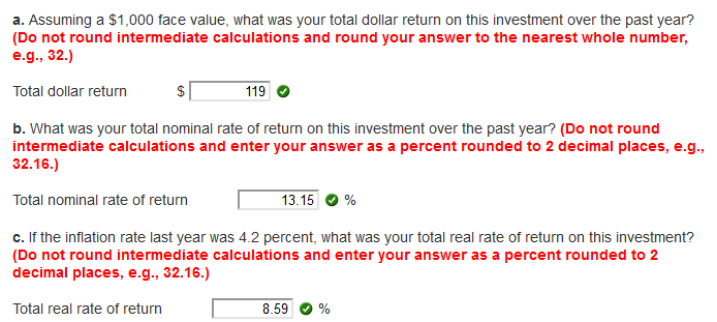
 

 
TDR
942 – 905 + 82 = 119
NROR
119 / 905 = .1314917127 (13.15%)
TROR
1 + .1315 / 1 + .042 – 1 = .08589 (8.59%)
 
Explanation:
a.
The total dollar return is the change in price plus the coupon payment, so:
 
Total dollar return = $942 – 905 + 82
Total dollar return = $119
 
b.
The nominal percentage return of the bond is:
 
R = ($942 – 905 + 82) / $905
R = .1315, or 13.15%
  
Notice here that we could have simply used the total dollar return of $119 in the numerator of this equation.
 
c.
Using the Fisher equation, the real return was:
   
(1 + R) = (1 + r)(1 + h)
 
r = (1.1315 / 1.042) – 1
r = .0859, or 8.59%
   
Consider the following information on large-company stocks for a period of years.
 

Series	Arithmetic Mean
Large-company stocks	11.9	%
Inflation	3.3

  
a. What was the arithmetic average annual return on large-company stocks in nominal terms?
(Do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.)
 
b. What was the arithmetic average annual return on large-company stocks in real terms?
(Do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.)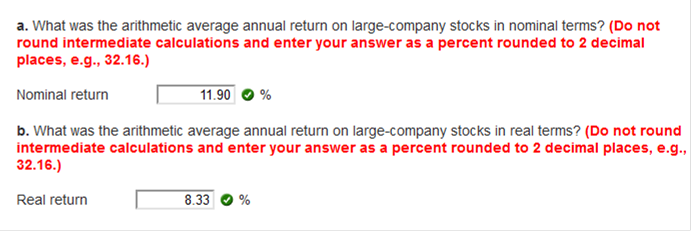

 
Explanation:
a.
The nominal return is the stated return, which is 11.9 percent.
b.
Using the Fisher equation, the real return was:
 
(1 + R) = (1 + r)(1 + h)
r = (1.1190) / (1.033) – 1
r = .0833, or 8.33%
   
Use the following returns for X and Y.
 

	Returns
Year	X					Y
1			21.5	%			25.5	%
2		–	16.5				–3.5
3			9.5				27.5
4			19.0				–14.0
5			4.5				31.5

 
Calculate the average returns for X and Y.
(Do not round intermediate calculations and enter your answers as a percent rounded to 2 decimal places, e.g., 32.16.)
Calculate the variances for X and Y.
(Do not round intermediate calculations and round your answers to 6 decimal places, e.g., 32.161616.)
Calculate the standard deviations for X and Y.
(Do not round intermediate calculations and enter your answers as a percent rounded to 2 decimal places, e.g., 32.16.)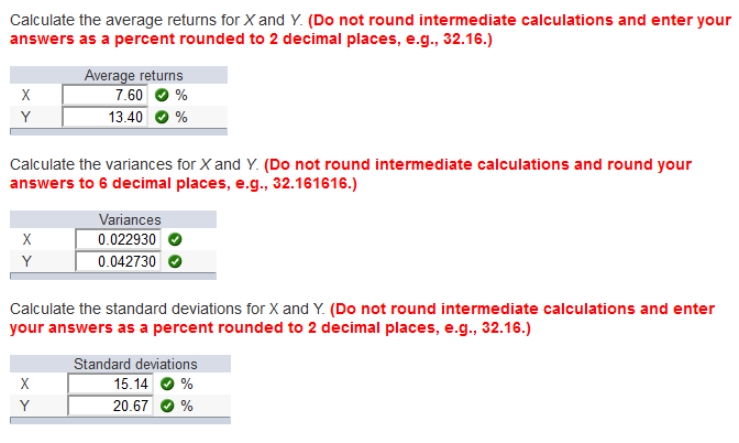

  
Explanation:
The average return is the sum of the returns, divided by the number of returns. The average return for each stock was:
 
X¯¯¯=[Σi=1Nxi] / N = [.215 − .165 + .095 + .190 + .045]5=.0760, 
or  7.60%X¯=[Σi=1Nxi]/N=[.215⁢ − .165⁢ + .095⁢ + .190⁢ + .045]5=.0760,⁢  or  7.60%
 
Y¯¯¯=[Σi=1Nyi]/N=[.255 − .035 + .275 − .140 + .315]5=.1340, 
or  13.40%Y¯=[Σi=1Nyi]/N=[.255⁢ − .035⁢ + .275⁢ − .140⁢ + .315]5=.1340,⁢  or  13.40%
 
We calculate the variance of each stock as:
 
σx2=[Σi=1N(xi−x¯)2]/(N−1)σx2=[Σi=1N(xi−x¯)2]/(N−1)

σx2=15−1{(.215−.0760)2+(−.165−.0760)2+(.095−.0760)2+(.190−.0760)2+(.045−.0760)2}=.022930σx2=
15−1{(.215−.0760)2+(−.165−.0760)2+(.095−.0760)2+(.190−.0760)2+(.045−.0760)2}=.022930

σy2=15−1{(.255−.1340)2+(−.035−.1340)2+(.275−.1340)2+(−.140−.1340)2+(.315−.1340)2}=.042730σy2=
15−1{(.255−.1340)2+(−.035−.1340)2+(.275−.1340)2+(−.140−.1340)2+(.315−.1340)2}=.042730
 
The standard deviation is the square root of the variance, so the standard deviation of each stock is:
  
σ_X = .022930^1/2
σ_X = .1514, or 15.14%
 
σ_Y = .042730^1/2
σ_Y = .2067, or 20.67%
   
You find a certain stock that had returns of 15.2 percent, –22.6 percent, 28.6 percent, and 19.6 percent for four of the last five years.
Assume the average return of the stock over this period was 13.2 percent.

What was the stock’s return for the missing year?
(Do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.)


What is the standard deviation of the stock’s returns?
(Do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.)
 

 
Explanation:
Here, we know the average stock return, and four of the five returns used to compute the average return.
We can work the average return equation backward to find the missing return. The average return is calculated as:

.1320 = (.152 – .226 + .286 + .196 + R) / 5
.66 = .152 – .226 + .286 + .196 + R
R = .2520, or 25.20%

The missing return has to be 25.20 percent. Now we can use the equation for the variance to find:

Variance = 1/4[(.152 – .132)² + (–.226 – .132)² + (.286 – .132)² + (.196 – .132)² + (.252 – .132)²]
Variance = .042694

And the standard deviation is:

Standard deviation = .042694^1/2
Standard deviation = .2066, or 20.66%
   
Assume the returns from holding small-company stocks are normally distributed.
Also assume the average annual return for holding the small-company stocks for a period of time was
16.1 percent and the standard deviation of those stocks for the period was 34.6 percent.
 
Use the NORMDIST function in Excel® to answer the following questions.

What is the approximate probability that your money will double in value in a single year?
(Do not round intermediate calculations and enter your answer as a percent rounded to 3 decimal places, e.g., 32.161.)

What is the approximate probability that your money will triple in value in a single year?
(Do not round intermediate calculations and enter your answer as a percent rounded to 8 decimal places, e.g., 32.16161616.)
 

Explanation:
The mean return for small company stocks was 16.1 percent, with a standard deviation of 34.6 percent.
Doubling your money is a 100% return, so if the return distribution is normal, we can use the z-statistic. So:

z = (X – µ) / σ
z = (100% – 16.1%) / 34.6% = 2.425 standard deviations above the mean
This corresponds to a probability of ≈ .766%, less than once every 100 years.
Tripling your money would be:
z = (200% – 16.1%) / 34.6% = 5.315 standard deviations above the mean
This corresponds to a probability of ≈ .00000533%.
= 1 - NORMDIST(100,16.1,34.6,TRUE) 0.766
= 1 - NORMDIST(200,16.1,34.6,TRUE)0.00000533%
   
One year ago, you purchased 600 shares of stock for $14 a share.
The stock pays $.41 a share in dividends each year. Today, you sold your shares for $15.30 a share.
What is your total dollar return on this investment?
 
$1,222
$7,43
$815
$780
$1,026
 
600 × (15.30 - 14 + .41) = 1,026
   
One year ago, you purchased a 6 percent coupon bond with a face value of $1,000 when it was selling
for 98.6 percent of par. Today, you sold this bond for 101.2 percent of par.
What is your total dollar return on this investment?
 
$86
$60
$64
$74
$82
 
 (1.012 × 1,000) - (.986 × 1,000) + (.06 × 1,000) = 86
   
Cox Footwear pays a constant annual dividend. Last year, the dividend yield was 3.2 percent when the stock
was selling for $35a share. What is the current price of the stock if the current dividend yield is 2.9 percent?
 
$18.92
$38.62
$25.20
$26.87
$27.40
 
.032 × 35 = 1.12
1.12 / .029 = 38.62
   
The Bermuda Triangle Store pays a constant dividend. Last year, the dividend yield was 4.0 percent
when the stock was selling for $16 a share. What must the stock price be today if the market currently
requires a 4.3 percent dividend yield on this stock?
 
$14.88
$12.30
$15.59
$19.22
$12.48
 
.040 × 16 = .64
.64 / .043 = 14.88
   
The stock of Southern United is priced at $52 a share and has a dividend yield of 3.6 percent.
The firm pays constant annual dividends.
What is the amount of the next dividend per share?
 
$1.826
$1.729
$1.872
$1.878
$1.724
 
.036 × 52 = 1.872
   
One year ago, you bought a stock for $29.15 a share. You received a dividend of $1.04 per share last
month and sold the stock today for $28.80 a share. What is the capital gains yield on this investment?
 
2.37 percent
1.76 percent
-1.20 percent
-1.62 percent
.53 percent
 
28.80 - 29.15) / 29.15 = -.0120, or -1.20 %
   
Hercules Movers pays a constant annual dividend of $1.48 per share on its stock. Last year at this time,
the market rate of return on this stock was 15.7 percent. Today, the market rate has fallen to 13.3 percent.
What would your capital gains yield have been if you had purchased this stock one year ago and then sold the stock today?
 
-15.29 percent
-22.03 percent
8.16 percent
16.47 percent
18.05 percent
 
(1.48 / .133) - (1.48 / .157)] / (1.48 / .157) = .1805, or 18.05%
   
One year ago, Debra purchased 5,400 shares of KNF stock for $218,056. Today, she sold those shares
for $19.49 a share. What is the capital gains yield on this investment if the dividend yield is 1.7 percent?
 
-28.01 percent
-48.82 percent
3.07 percent
-51.73 percent
4.53 percent
 
19.49 - (218,056 / 5,400)] / (218,056 / 5,400) = -.5173 or -51.73%
   
Lamey Gardens has a dividend growth rate of 5.6 percent, a market price of $13.16 a share,
and a required return of 14 percent.  What is the amount of the last dividend this company paid?
 
$1.05
   
Sweet Treats pays a constant annual dividend of $2.38 a share and currently sells for $52.60 a share.
What is the rate of return?
 
4.52 percent
 
2.38 / 52.60 = .0452, or 4.52%
   
Healthy Foods just paid its annual dividend of $1.62 a share.
The firm recently announced that all future dividends will be increased by 2.1 percent annually.
What is one share of this stock worth to you if you require a rate of return of 15.7 percent?
 
$12.16
 
 (1.62 x 1.021) / (.157-.021) = 12.16
   
Braxton's Cleaning Company stock is selling for $32.60 a share based on a rate of return of 13.8 percent.
What is the amount of the next annual dividend if the dividends are increasing by 2.4 percent annually?
 
$3.72
 
32.60 x (.138-.024) = 3.72
   
Horseshoe Stables is losing significant market share and thus its managers have decided to decrease the firm's annual dividend.
The last annual dividend was $.86 a share but all future dividends will be decreased by 3.5 percent annually.
What is a share of this stock worth today at a required return of 17.8 percent?
 
$3.90
 
.86 x (1 -.035) / .178 - (-.035) = 3.90
   
The Sports Club plans to pay an annual dividend of $1.20 per share next year, $1.12 per share a year for the following two years,
and then a final liquidating dividend of $14.20 per share four years from now. How much is one share of this stock worth to you
today if you require a rate of return of 18.7 percent of this risky investment?
 
$9.63
 
 (1.20 / 1.1871) + (1.12 / 1.1872) + (1.12 / 1.1873) + (14.20 / 1.1874) = 9.63
   
You would like to invest $24,000 and have a portfolio expected return of 11.5 percent.
You are considering two securities, A and B. Stock A has an expected return of 18.6 percent and B has
an expected return of 7.4 percent.
Approximately how much should you invest in Stock A if you invest the balance in Stock B?
 
a. $8,626
b. $7,807
c. $7,137
d. $7,411
e. $8,786
 
0.115 = 0.186x + 0.074(1 - x) x = 0.3661
0.3661 × 24,000 = 8,786
   
One year ago, you purchased 600 shares of stock for $14 a share. The stock pays $.41 a share in dividends each year.
Today, you sold your shares for $15.30 a share. What is your total dollar return on this investment?
 
$1,026
 
600 x (15.30 -14 + .41) = 1,026
   
 
Hercules Movers pays a constant annual dividend of $1.48 per share on its stock.
Last year at this time, the market rate of return on this stock was 15.7 percent. Today, the market rate has fallen to 13.3 percent.
What would your capital gains yield have been if you had purchased this stock one year ago and then sold the stock today?
 
18.05 percent
 
(1.48 / .133) - (1.48 / .157) / (1.48 / .157) = .1805, or 18.05%
   
S&S stock is expected to return 17.5 percent in a booming economy, 12.4 percent in a normal economy,
and 1.2 percent in a recession. The probabilities of an economic boom, normal state, or recession are
2 percent, 90 percent, and 8 percent, respectively. What is the expected rate of return on this stock?
 
11.61%
 
(.02 x.175) + (.90 x.124) + (.08 x.012) = .1161, or 11.61
 
You own a portfolio that is invested 43 percent in Stock A, 16 percent in Stock B, and the remainder in Stock C.
The expected returns on stocks A, B, and C are 9.1 percent, 16.7 percent, and 11.4 percent, respectively.
What is the expected return on the portfolio?
 
11.26 percent
 
[.43 .091] + [.16 .167] + [(1 -.43 -.16) .114] = .1126, or 11.26%
   
You would like to invest $24,000 and have a portfolio expected return of 11.5 percent. You are
considering two securities, A and B. Stock A has an expected return of 18.6 percent and B has
an expected return of 7.4 percent.
Approximately how much should you invest in Stock A if you invest the balance in Stock B?
 
$8,786
 
.115 = .186x + .074 = .3661
.3661 x 24,000 = 8,786
   
 
BJB stock has an expected return of 17.82 percent.
The risk-free rate is 4.6 percent and the market risk premium is 8.2 percent.
What is the stock's beta?
 
a. 1.68
b. 1.48
c. 1.47
d. 1.51
e. 1.61
   
Bruno's stock should return 14 percent in a boom, 11 percent in a normal economy, and 4 percent in
a recession. The probabilities of a boom, normal economy, and recession are 8 percent, 90 percent,
and 2 percent, respectively. What is the variance of the returns on this stock?
 
a. .000169
b. .011561
c. .001506
d. .001538
e. .011387
 
Expected return = (.08 ×.14) + (.90 ×.11) + (.02 ×.04) = .111
Variance = .08(.14 -.111)2 + .90(.11 -.111)2 + .02(.04-.111)2 = .000169
   
A stock has a beta of 1.32, the expected return on the market is 12.72, and the risk-free rate
is 4.05. What must the expected return on this stock be
 
15.49 percent
 
0405 + 1.32(.1272 -.0405) = .1549, or 15.49%
 
You have compiled the following information on your investments.
What rate of return should you expect to earn on this portfolio?
 
Value A = 400 $24 =                        $9,600
Value B = 300 $13 =                         $3,900
Value C = 100 $33 =                         $3,300
Value D = 100 $54 =                        $5,400.
 
10.09%
 
9,600 + 3,900 + 3,300 + 5,400 = 22,200
(9,600 / 22,200)(.136) + (3,900 / 22,200)(.148) + (3,300 / 22,200)(.074) + [($5,400 /$22,200) .021] = .1009, or 10.09 percent
   
A stock has a beta of 1.32 and an expected return of 12.8 percent. The risk-free rate is 3.6 percent.
What is the slope of the security market line?
 
a. 7.99 percent
b. 9.03 percent
c. 6.49 percent
d. 7.28 percent
e. 6.97 percent
 
Slope = (.128 -.036)/1.32 = .0697, or 6.97 percent
   
Ben & Terry's has an expected return of 13.2 percent and a beta of 1.08.
The expected return on the market is 12.4 percent. What is the risk-free rate?
 
2.4 %
 
1.32 + 1.08 = 2.40
   
Stock A has an expected return of 14.4 percent and a beta of 1.21.
Stock B has an expected return of 12.87 percent and a beta of 1.06.
Both stocks have the same reward-to-risk ratio. What is the risk-free rate?
 
a. 2.28 percent
b. 1.92 percent
c. 3.35 percent
d. 2.06 percent
e. 1.79 percent
 
(.144-Rf)/1.21 = (.1287-Rf)/1.06
Rf = .0206, or 2.06 percent
   
Southern Wear stock has an expected return of 15.1 percent. The stock is expected to lose 8 percent in a recession
and earn 18 percent in a boom. The probabilities of a recession, a normal economy, and a boom are 2 percent,
87 percent, and 11 percent, respectively. What is the expected
return on this stock if the economy is normal?
 
a. 16.43 percent
b. 17.04 percent
c. 14.79 percent
d. 15.26 percent
e. 11.08 percent
15.26 percent
 
E(R) = .151 = (.02 ×-.08) + (.87 ×x) + (.11 ×.18)
x = .1526, or 15.26 percent
   
Bama Entertainment has common stock with a beta of 1.22. The market risk premium is 8.1 percent
and the risk-free rate is 3.9 percent. What is the expected return on this stock?
 
a. 12.67 percent
b. 12.40 percent
c. 14.13 percent
d. 13.31 percent
e. 13.78 percent
 
E(R) = .039 + 1.22(.081) = .1378, or 13.78 percent
   
You own a $36,800 portfolio that is invested in Stocks A and B. The portfolio beta is equal to the market beta.
Stock A has an expected return of 22.6 percent and has a beta of 1.48. Stock B has a beta of .72.
What is the value of your investment in Stock A?
 
a. $8,619
b. $14,500
c. $12,333
d. $17,204
e. $13,558
   
You own a $58,600 portfolio comprised of four stocks. The values of
Stocks A, B, and C are $11,200, $17,400, and $20,400, respectively. What
is the portfolio weight of Stock D?
 
a. 16.38 percent
b. 12.58 percent
c. 15.39 percent
d. 10.33 percent
e. 12.10 percent
16.38 percent
 
58,600 - 11,200 - 17,400 - 20,400) / 58,600 = .1638, or 16.38
   
A stock has produced returns of 19 percent, 6 percent, -21 percent, -2 percent, and 14 percent for the past five years, respectively.
What is the standard deviation of these returns?
 
16.64 percent
14.65 percent
9.23 percent
8.87 percent
15.71 percent
 
Average return = [19+6-21-2+14]/5
= 16/5
= 3.2%
Standard deviation =square root of [(19-3.2)²+ (6-3.2)²+(-21-3.2)²+(-2-3.2)²+ (14-3.2)²]/5
=SR [249.64+ 7.84+ 585.64+ 27.04+ 116.64]/5
=SR [ 986.8/5]
SD = SR 197.36= 14.05%
   
S&S stock is expected to return 17.5 percent in a booming economy, 12.4 percent in a normal economy, and
1.2 percent in a recession. The probabilities of an economic boom, normal state, or recession are 2 percent,
90 percent, and 8 percent, respectively. What is the expected rate of return on this stock?
 
a. 11.89 percent
b. 11.61 percent
c. 10.50 percent
d. 12.43 percent
e. 12.56 percent
 
Expected return = (.02 ×.175) + (.90 ×.124) + (.08 ×.012) = .1161, or 11.61 percent
   
You own a stock that has an expected return of 15.72 percent and a beta of 1.33. The U.S.
Treasury bill is yielding 3.82 percent, and the inflation rate is 2.95 percent. What is the expected rate of return on the market?
 
a. 12.07 percent
b. 13.42 percent
c. 13.64 percent
d. 12.77 percent
e. 14.09 percent
 
E(R) = .1572 = .0382 + 1.33(Rm-.0382)     Rm = .1277, or 12.77 percent
   
You own a portfolio of two stocks, A and B. Stock A is valued at $84,650 and has an expected return of
10.6 percent. Stock B has an expected return of 6.4 percent. What is the expected return on the portfolio if
the portfolio value is $97,500?
 
a. 9.74 percent
b. 9.99 percent
c. 10.05 percent
d. 10.09 percent
e. 9.62 percent
 
ValueB = 97,500 - 84,650 = 12,850
Expected return = [(84,650/$97,500) × .106] + [(12,850 / 97,500) × .064] = .1005 or 10.05 percent
   
The risk-free rate is 3.7 percent and the expected return on the market is 12.3 percent.
Stock A has a beta of 1.1 and an expected return of 13.1 percent.
Stock B has a beta of .86 and an expected return of 11.4 percent. Are these stocks correctly priced?
Why or why not?
 
a. No, Stock A is overpriced but Stock B is correctly priced.
b. No, Stock A is overpriced and Stock B is underpriced.
c. No, both stocks are overpriced.
d. No, Stock A is underpriced and Stock B is overpriced.
e. No, Stock A is underpriced but Stock B is correctly priced.
 
E(RA) = .037 + 1.1(.123 -.037) = .1316, or 13.16 percent
E(RB) = .037 + .86(.123 -.037) = .1110, or 11.10 percent
Stock A is overpriced because its expected return lies below the security market line.
Stock B is underpriced because its expected return lies above the security market line.