|
Accounting | Business | Computer
Science | General
Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out
Intermediate Accounting (ACG 3101) Homework 5 Intermediate Accounting Homework 1 2 3 4 5 6 7 8 9 10 11 | Exams Chapters 1-3 4-7 8-9 10-11 | Final Exam
Required information
Learning Objective 05-03 Compute the present value of a single amount. Skip to question [The following information applies to the questions displayed below.] The present value of a single amount is the amount of money today that is equivalent to a given amount to be received or paid in the future. It is computed by dividing the future amount by (1 + i)n. The Present Value of $1 table simplifies the calculation of the present value of any future amount. Present value of a single amount What is the present value of $5,000 to be received five years from now, assuming an interest rate of 8%? (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) Multiple Choice $3,402.90 $7,346.67 $3,756.55 $6,655.04 Explanation Following the 8% interest rate column down to the fifth period gives the present value factor of 0.68058. Multiply the $5,000 future value times the present value factor of 0.68058 to get $3,402.90. Remember, the present value will always be less that the future value because of interest (Present value of $1). Required information Learning Objective 05-08 Compute the present value of an ordinary annuity, an annuity due, and a deferred annuity. Skip to question [The following information applies to the questions displayed below.] The present value of an ordinary annuity (PVA) is the present value of a series of equal-sized cash flows with the first payment taking place at the end of the first compounding period. The present value of an annuity due (PVAD) is the present value of a series of equal-sized cash flows with the first payment taking place at the beginning of the annuity period. The present value of a deferred annuity is the present value of a series of equal-sized cash flows with the first payment taking place more than one time period after the date of the agreement. (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) What is the present value of $6,000 to be paid at the end of each of the next eight periods assuming an interest rate of 10%? Multiple Choice $35,211 $75,477 $68,615 $32,010 Explanation An annuity is a series of equal payments. If the payments come at the end of each period, they represent an ordinary annuity. We use the present value of an annuity (PVA) table for ordinary annuities. Multiply the payment of $6,000 per period times the present value of an ordinary annuity interest factor in the 10% column and the eighth row: $6,000 × 5.33493 = $32,010. What is the present value of $6,000 to be paid at the beginning of each of the next eight periods assuming an interest rate of 10%? Multiple Choice $35,211 $75,477 $68,615 $32,010 Explanation An annuity is a series of equal payments. If the payments come at the beginning of each period, they represent an annuity due. We use the present value of an annuity due (PVAD) table for annuities due. Multiply the payment of $6,000 per period times the present value of an annuity due interest factor in the 10% column and the eighth row: $6,000 × 5.86842 = $35,211. What is the present value of $6,000 to be received at the end of each of eight periods, assuming the first payment occurs at the end of the fourth year and an interest rate of 10%? Multiple Choice $36,454 $24,049 $32,010 $38,970 Explanation Knowledge Check 01 An annuity is a series of equal payments. If the payments come at the end of each period, it is an ordinary annuity. When the first payment does not begin immediately, it is a deferred annuity. Finding the present value of a deferred annuity involves a two-step process: 1. Calculate the present value of the ordinary annuity: PVA (i = 10%, n = 8) = $6,000 × 5.33493 = $32,010. This is the present value of the annuity as of the beginning of the fourth year. 2. Calculate the present value of the amount in Step 1.: PV (i = 10%, n = 3) = $32,010 × 0.75131 = $24,049. This is the present value of the amount in Step 1 from the beginning of the fourth year to the beginning of the first year (today). Learning Objective 05-09 Solve for unknown values in annuity situations involving present value. Skip to question [The following information applies to the questions displayed below.] In present value problems involving annuities, there are four variables: PVA or PVAD, the annuity amount, the number of compounding periods (n) and the interest rate (i). If you know any three of these, you can determine the fourth. If you borrow $30,000 from the bank for 5 years (60 months) at 12% interest, you would calculate the payment required at the end of each month by: Multiple Choice Multiplying $30,000 by the present value of $1, where i = 12% and n = 5. Dividing $30,000 by the present value of an ordinary annuity of $1, where i = 1% and n = 60. Dividing $30,000 by the present value of an ordinary annuity of $1, where i = 12% and n = 5. Dividing $30,000 by the future value of an ordinary annuity of $1, where i = 1% and n = 60. Explanation Since you make the payments at the end of each month, you have an ordinary annuity. To calculate the payments, find the present value of an ordinary annuity factor for 60 months at 1% per period (12% annual rate ÷ 12 months) and divide the loan amount by that present value factor. Required information Learning Objective 05-10 Briefly describe how the concept of the time value of money is incorporated into the valuation of bonds, long-term leases, and pension obligations. Skip to question [The following information applies to the questions displayed below.] Most accounting applications of the time value of money involve the present values of annuities. The initial valuation of long-term bonds and the present value of the lump-sum payment Certain leases require the lessee to compute the present value of future lease payments to value the leased asset and corresponding lease obligation. Similarly, installment notes sometimes require us to calculate the present value of installment payments (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) Mufala, Inc., will issue $10,000,000 of 6% 10-year bonds. The market rate for bonds with similar risk and maturity is 8%. Interest will be paid by Mufala semiannually. What is the issue price of the bonds? (Round your answer to nearest whole dollar.)  8,640,999 Explanation Interest payment = $10,000,000 × 3% (6% ÷ two semiannual payments) = $300,000 n = 20 (10 years × two semiannual payments); i = 4% (8% market rate ÷ 2 semiannual payments) PVA = $300,000 × 13.59033 (n = 20, i = 4%) = $4,077,099 PV of the $10,000,000 face amount that will be received in 10 years: n = 20 (10 years × two semiannual payments); i = 4% (8% market rate ÷ 2 semiannual payments) PV = $10,000,000 × 0.45639 (n = 20, i = 4%) = $4,563,900 $4,077,099 + $4,563,900 = $8,640,999 Present and future value tables of $1 at 11% are presented below.
Lorien, Inc. leased tree excavators under terms of $10,000 down and four equal annual payments of $30,000 on the anniversary date of the lease. The interest rate implicit in the lease is 11%. For what amount would Lorien initially record the asset and lease liability? Multiple Choice $130,000 $103,074 $113,311 $93,074 Explanation Knowledge Check 01 Present Value of an Ordinary Annuity = $30,000 × 3.10245* = $93,074 Add the $10,000 down payment already at present value: $93,074 + $10,000 = $103,074 *PVA: n = 4; i = 11% The City of Smithfield’s pension fund is projecting the amount necessary today to fund an employee’s pension benefits. The employee has worked for the city for 10 years and will retire in 30 years from now. Retirement payments are expected to last for a total of 20 years and payments will be made to the employee at the end of each retirement year. Which of the following best describes the computation of the amount needed at the end of year 10 to fund the retiree’s annuity due to her 10 years of service to date? Multiple Choice Future value of $1 for 30 periods, times the present value of an ordinary annuity of 20 payments, times the annual annuity payment. Present value of $1 for 10 periods, times the present value of an ordinary annuity of 20 payments, times the annual annuity payment. Present value of $1 for 30 periods, times the present value of an ordinary annuity of 20 payments, times the annual annuity payment. Future value of $1 for 10 periods, times the present value of an ordinary annuity of 20 payments, times the annual annuity payment. Which concept means that money can be invested today to earn interest and grow to a larger amount in the future? Time Value of Money Concept The amount paid for the use of money for some period of time is referred to as ________. Interest _______ interest is calculated by multiplying an initial investment times the applicable interest rate and the period of time the money is used, whereas ________ interest involves earning interest on the interest. Simple, Compound On January 1, McLean Corp. borrowed $50,000 with 8% simple interest. What is the amount of interest that must be repaid at year-end? $4,000 50,000 x 8% x (12/12) = 4,000 The initial investment multiplied by the applicable interest rate and multiplied again by the period of time for which the money is used is referred to as ______ interest. Simple True or false: The time value of money means that money can be invested today to earn interest and grow to a larger amount in the future. True The amount of money that a dollar will grow to at some point in the future is known as the future value. Jim borrows $1,000 and has to repay $1,100 at the end of the year. The $100 payment is referred to as _____. interest Karr Company borrowed $100,000 by signing a 5-year note payable at 8% interest. At the end of year 5, Karr will repay the bank $146,933. At the time the note is signed, the $100,000 is referred to as the ______ of the note payable. present value Over a 5-year period, simple interest is ______ compound interest on the same note. less than Norton loans a customer $500 on January 1. On July 1 of the same year, the customer must repay Norton $525. The amount of interest earned by Norton is $_____. 25 Which of the following are required to compute the present value of a known future amount? (Select all that apply.) interest rate future value number of compounding periods Simple interest is computed by multiplying which of the following? (Select all that apply.) Period of time Initial investment Applicable interest rate Most monetary assets are valued at the ______ value of ______ cash flows. present future Alex would like to deposit $1,000 in the bank today and would like to know what that will grow in 5 years. Alex needs to compute the ______ value of the money future A series of payments in the same amount is referred to as annuity. $1,000 invested today at 10% compounded annually will grow to $1,100 at the end of one year or $1,210 at the end of two years. What is the initial $1,000 referred to as? Present value The future value of an ordinary annuity table is used when calculating The future value of a series of payments Lenny borrowed $10,000 on a 5-year interest bearing note with an interest rate of 10%. At the end of 5 years, Lenny must repay the bank $16,105. Based on the amount that must be repaid, interest was calculated with what type of interest rate? Compound Interest Milo decides to invest $1,500 in a savings account every year at the beginning of the year for 10 years. Assuming an interest rate of 7%, how much will Milo have at the end of the 10th year? $22,175 $1,500 X 14.7836 (i.e., FVAD, the future value of annuity due, factor at 7% for 10 periods) = $22,175 To solve for the present value of a single sum, you need to know the future value, the number of compounding periods, and the _____ _____. interest rate Jean expects to receive $5,000 at the end of each year for 4 years. The annuity has an interest rate of 7%. The present value of this annuity at Time Zero, the inception of the annuity (rounded to the nearest dollar) is $16,936 The present value ordinary annuity factor of 7% for 4 periods is 3.38721. $5,000 x 3.38721 = $16,936. Which of the following is an example of a monetary asset? Accounts Receivable On a financial calculator, the PMT key is used to input the annuity payment A fixed payment at fixed intervals is called an annuity Which of the following are the four variables in present value annuity problems? The interest rate The number of periods The present value The payment amount Which of the following situations would involve the calculation of the future value of an ordinary annuity? Depositing an amount to a savings account each month that will grow to purchase a car in 5 years. Which of the following accounts uses time value of money concepts to value the account? Long-term bonds George will deposit $2,000 in a savings account at the beginning of each year for 8 years. Assuming the interest rate is 5%, how much money will George have in the account at the end of year 8? Round your answer to the nearest dollar. $20,053 $2,000 x 10.0266 (i.e., FVAD, the future value of annuity due, factor at 5% for 8 periods) = $20,053 The _____ rate of interest on a bond is the interest rate printed on the bond; the ______ rate of interest is the current rate of interest being paid on investments with similar characteristics. stated; market Carol expects to receive $1,000 at the end of each year for 5 years. The annuity has an interest rate of 10%. The present value of this annuity at Time Zero, the inception of the annuity (rounded to the nearest dollar) is $3,791 The present value ordinary annuity factor of 10% for 5 periods is 3.79079. $1,000 x 3.79079 = $3,791 Jenson rents equipment by signing a contract to pay $1,000 per month at the beginning of each month. The first payment is due upon signing the contract. The lease is a(n) annuity due. Match each abbreviation on a financial calculator to its function. N - Number of periods %I - Interest rat PV - Present value FV - Future value PMT - annuity payment CPT – Compute True or false: Present value calculations are used in calculating pension contributions for defined benefit plans. True Assume you borrow $10,000 from the bank and promise to repay the amount in 5 equal installments beginning one year from today. The stated interest rate on the loan is 5%. What is the unknown variable in this problem? The payment amount. The amount of money that a dollar will grow to at some point in the future is the future value of a single amount. Which of the following items require time value of money concepts? (Select all that apply.) capital leases pensions bonds payable True or false: At the date of issue, the stated rate of interest on the bond is always equal to the market rate of interest on the bond. False True or false: A lease is an annuity when it requires equal payments at the same interval. True Valuing defined benefit pension obligation typically requires the calculation of the present value of a _____ _____. deferred annuity The formula FV = $1(1+i)n is used to calculate the future value of $1. Exercise 5-1 (Algo) Future value; single amount [LO5-2] Determine the future value of the following single amounts (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1 (Use appropriate factor(s) from the tables provided.) (Round your final answers to nearest whole dollar amount.): 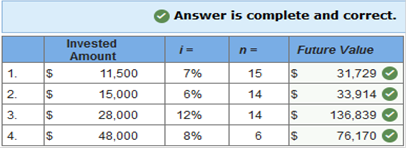 Explanation 1. FV = $11,500 (2.75903*) = $31,729 *Future value of $1: n = 15, i = 7% (from FV of $1) 2. FV = $15,000 (2.26090*) = $33,914 *Future value of $1: n = 14, i = 6% (from FV of $1) 3. FV = $28,000 (4.88711*) = $136,839 *Future value of $1: n = 14, i = 12% (from FV of $1) 4. FV = $48,000 (1.58687*) = $76,170 *Future value of $1: n = 6, i = 8% (from FV of $1) Exercise 5-10 (Algo) Future and present value [LO5-3, 5-7, 5-8] Answer each of the following independent questions. Alex Meir recently won a lottery and has the option of receiving one of the following three prizes: (1) $74,000 cash immediately, (2) $26,000 cash immediately and a six-period annuity of $8,300 beginning one year from today, or (3) a six-period annuity of $15,000 beginning one year from today. (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) 1. Assuming an interest rate of 6%, determine the present value for the above options. Which option should Alex choose? 2. The Weimer Corporation wants to accumulate a sum of money to repay certain debts due on December 31, 2030. Weimer will make annual deposits of $140,000 into a special bank account at the end of each of 10 years beginning December 31, 2021. Assuming that the bank account pays 7% interest compounded annually, what will be the fund balance after the last payment is made on December 31, 2030? Assuming an interest rate of 6%, determine the present value for the above options. Which option should Alex choose? (Round your final answers to nearest whole dollar amount.) 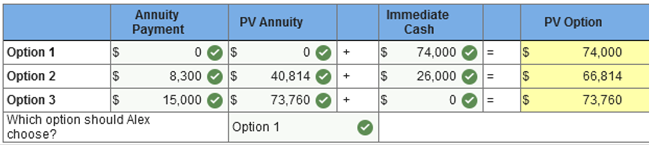 The Weimer Corporation wants to accumulate a sum of money to repay certain debts due on December 31, 2030. Weimer will make annual deposits of $140,000 into a special bank account at the end of each of 10 years beginning December 31, 2021. Assuming that the bank account pays 7% interest compounded annually, what will be the fund balance after the last payment is made on December 31, 2030? (Round your final answers to nearest whole dollar amount.)  Explanation 1. Choose the option with the highest present value. (1) PV = $74,000 (2) PV = $26,000 + $8,300 (4.91732*) *Present value of an ordinary annuity of $1: n = 6, i = 6% (from PVA of $1) PV = $26,000 + $40,814 = $66,814 (3) PV = $15,000 (4.91732*) = $73,760 *Present value of an ordinary annuity of $1: n = 6, i = 6% (from PVA of $1) Alex should choose option (1). 2. FVA = $140,000 (13.8164*) = $1,934,300 *Future value of an ordinary annuity of $1: n = 10, i = 7% (from FVA of $1) Exercise 5-6 (Static) Noninterest-bearing note; single payment [LO5-5] The Field Detergent Company sold merchandise to the Abel Company on June 30, 2021. Payment was made in the form of a noninterest-bearing note requiring Abel to pay $85,000 on June 30, 2023. Assume that a 10% interest rate properly reflects the time value of money in this situation. (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) Required: Calculate the amount at which Field should record the note receivable and corresponding sales revenue on June 30, 2021. (Round your final answers to nearest whole dollar amount.) 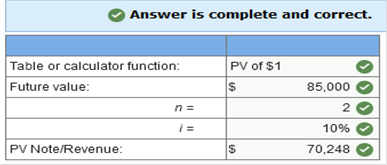 Explanation PV = $85,000 (0.82645*) = $70,248 = Note/revenue *Present value of $1: n = 2, i = 10% (from PV of $1) Exercise 5-12 (Static) Future value; solving for annuities and single amount [LO5-4, 5-9] John Rider wants to accumulate $100,000 to be used for his daughter’s college education. He would like to have the amount available on December 31, 2026. Assume that the funds will accumulate in a certificate of deposit paying 8% interest compounded annually. (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) Answer each of the following independent questions. Required: 1. If John were to deposit a single amount, how much would he have to invest on December 31, 2021? 2. If John were to make five equal deposits on each December 31, beginning a year later, on December 31, 2022, what is the required amount of each deposit? 3. If John were to make five equal deposits on each December 31, beginning now, on December 31, 2021, what is the required amount of each deposit? (For all requirements, Round your final answers to nearest whole dollar amount.) 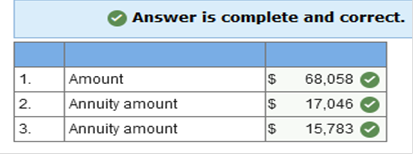 Explanation 1. PV = $100,000 (0.68058*) = $68,058 *Present value of $1: n = 5, i = 8% (from PV of $1) 2.
*Future value of an ordinary annuity of $1: n = 5, i = 8% (from FVA of $1) Annuity amount = $17,046 3.
*Future value of an annuity due of $1: n = 5, i = 8% (from FVAD of $1) Annuity amount = $15,783 Exercise 5-7 (Static) Concepts; terminology [LO5-1, 5-2, 5-3, 5-6] Listed below are several terms and phrases associated with concepts discussed in the chapter. Pair each item from List A (by letter) with the item from List B that is most appropriately associated with it.  Problem 5-11 (Algo) Solving for unknown lease payment [LO5-9, 5-10] Benning Manufacturing Company is negotiating with a customer for the lease of a large machine manufactured by Benning. The machine has a cash price of $920,000. Benning wants to be reimbursed for financing the machine at a 9% annual interest rate. (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) Required: 1. Determine the required lease payment if the lease agreement calls for 12 equal annual payments beginning immediately. 2. Determine the required lease payment if the first of 12 annual payments will be made one year from the date of the agreement. 3. Determine the required lease payment if the first of 12 annual payments will be made immediately and Benning will be able to sell the machine to another customer for $62,000 at the end of the 12-year lease. 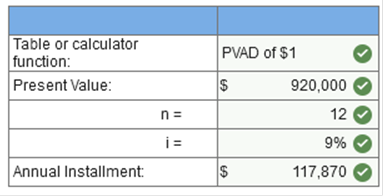   PVAD Table: 920000 / 7.80519 PVA Table: 920000 / 7.16073 7.80519 = $ 920,000 - $62,000 * 0.35553 7.80519 = $ 897,956.85 897,956.85 / 7.80519 = $ 115,046.11 Explanation 1. PVAD = Annuity amount × Annuity factor
*Present value of an annuity due of $1: n = 12, i = 9% (from PVAD of $1) Annuity amount = $117,870 = Lease payment 2.
*Present value of an ordinary annuity of $1: n = 12, i = 9% (from PVA of $1) Annuity amount = $128,479 = Lease payment 3. PVAD = (Annuity amount × Annuity factor) + PV of residual
PV of residual = $62,000 × 0.35553* = $22,043 *Present value of $1: n = 12, i = 9% (from PV of $1)
Present value of an annuity due of $1: n = 12, i = 9% (from PVAD of $1) Annuity amount = $115,046 = Lease payment TB MC Qu. 5-51 (Static) Spielberg Inc. signed a $200,000… Present and future value tables of $1 at 11% are presented below.
Spielberg Inc. signed a $200,000 non-interest bearing note due in five years from a production company eager to do business. Comparable borrowings have carried an 11% interest rate. What is the value of this debt at its inception? $118,690 Explanation PV = $200,000 × 0.59345* = $118,690 *PV of $1: n = 5; i = 11% TB Problem 5-103 (Static) Pockets lent $20,000 to Lego Construction on January 1, 2021. Lego signed a three-year, 5% installment note to be paid in three equal payments at the end of each year. (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) Required: Calculate the amount of one installment payment. (Round your final answer to the nearest whole dollar.) $7,344 Explanation Installment payment calculation
On January 1, 2021, Mania Enterprises issued 12% bonds dated January 1, 2021, with a face amount of $20 million. The bonds mature in 2033 (10 years). For bonds of similar risk and maturity, the market yield is 10%. Interest is paid semiannually on June 30 and December 31. (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) Required: Determine the price of the bonds at January 1, 2021. (Enter your answer in whole dollars.)  Explanation
TB MC Qu. 5-63 (Static) Which of the following must be known in order... Which of the following must be known in order to compute the interest rate when financing an asset purchase with an annuity? Present value of the annuity, dollar amount and timing of the annuity payments. TB MC Qu. 5-50 (Static) LeAnn wishes to know how much she should inv... LeAnn wishes to know how much she should invest now at 7% interest in order to accumulate a sum of $5,000 in four years. She should use a table for the: Present value of $1. TB MC Qu. 5-57 (Static) A series of equal periodic payments that... A series of equal periodic payments that starts more than one period after the agreement is called: A deferred annuity. Brief Exercise 5-6 (Algo) Future value; ordinary annuity [LO5-7] Leslie McCormack is in the spring quarter of her freshman year of college. She and her friends already are planning a trip to Europe after graduation in a little over three years. Leslie would like to contribute to a savings account over the next three years in order to accumulate enough money to take the trip. Assume an interest rate of 16%, compounded quarterly. (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) How much will she accumulate in three years by depositing $520 at the end of each of the next 12 quarters, beginning three months from now? (Round your interest rate to 1 decimal place.) 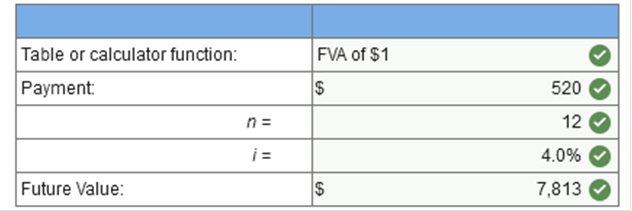 Explanation Interest is paid for 12 periods at 4.00% (one-quarter of the annual rate). FVA = $520 (15.0258*) = $7,813 *Future value of an ordinary annuity of $1: n = 12, i = 4.00% (from FVA of $1) Brief Exercise 5-10 (Algo) Deferred annuity [LO5-8, 5-10] Canliss Mining Company borrowed money from a local bank. The note the company signed requires five annual installment payments of $14,000 not due for three years. The interest rate on the note is 7%. (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) What amount did Canliss borrow? (Do not round intermediate calculations. Round your final answers to nearest whole dollar amount.)  Explanation PVA = $14,000 × 4.10020* = $57,403 *Present value of an ordinary annuity of $1: n = 5, i = 7% (from PVA of $1) PV = $57,403 × .87344* = $50,138 *Present value of $1: n = 2, i = 7% (from PV of $1) Brief Exercise 5-8 (Algo) Present value; ordinary annuity; installment notes [LO5-8, 5-10] Canliss Mining Company borrowed money from a local bank. The note the company signed requires five annual installment payments of $16,500 beginning one year from today. The interest rate on the note is 7%. (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided.) What amount did Canliss borrow? (Round your final answers to nearest whole dollar amount.) 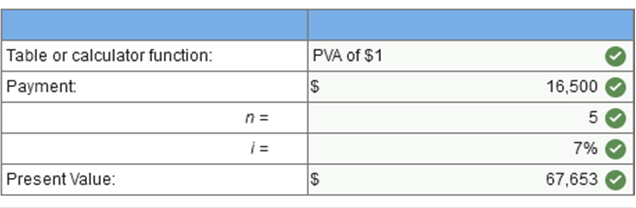 Explanation PVA = $16,500 (4.10020*) = $67,653 *Present value of an ordinary annuity of $1: n = 5, i = 7% (from PVA of $1) Exercise 5-5 (Algo) Solving for unknowns; single amounts [LO5-4] For each of the following situations involving single amounts, solve for the unknown. Assume that interest is compounded annually. (i = interest rate, and n = number of years) (FV of $1, PV of $1, FVA of $1, PVA of $1, FVAD of $1 and PVAD of $1) (Use appropriate factor(s) from the tables provided. Round your final answers to nearest whole dollar amount.) 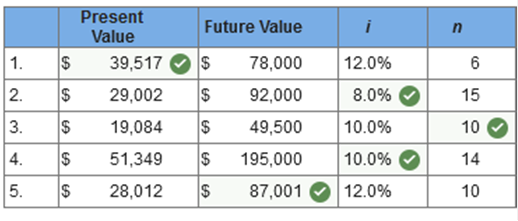 Explanation 1. PV = $78,000 (0.50663*) = $39,517 *Present value of $1: n = 6, i = 12.0% (from PV of $1) 2.
*Present value of $1: n = 15, i = ? (from PV of $1, i approximately 8.0%) 3.
*Present value of $1: n = ?, i = 10.0% (from PV of $1, n approximately 10 years) 4.
*Present value of $1: n = 14, i = ? (from PV of $1, i approximately 10.0%) 5. FV = $28,012 (3.10585*) = $87,000 *Future value of $1: n = 10, i = 12.0% (from FV of $1) Intermediate Accounting Homework 1 2 3 4 5 6 7 8 9 10 11 | Exams Chapters 1-3 4-7 8-9 10-11
| Final Exam
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |