|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Elementary Statistics Homework 1 2 3 4
5-6 6.3-7
8-10 | Tests Chapter 1-3
4 5-6 6.3-7 8-10 Final Review
Elementary Statistics (STA2023) Homework 4 If A denotes some event, what does Upper A overbar denote? If P(A)equals 0.005, what is the value of P (A)? What does Upper A overbar denote? Events A and Upper A overbar share all outcomes. Event Upper A overbar is always unusual. Event Upper A overbar denotes the complement of event A, meaning that Upper A overbar consists of all outcomes in which event A does not occur. Event Upper A overbar denotes the complement of event A, meaning that Upper A overbar and A share some but not all outcomes. If P(A) equals 0.005, what is the value of P(A)? (Type an integer or a decimal. Do not round.) P(A) = 0.995 P(A) = 1 - P(A) = 1.00 - 0.005 = .995 Which of the following values cannot be probabilities? Select all the values that cannot be probabilities. 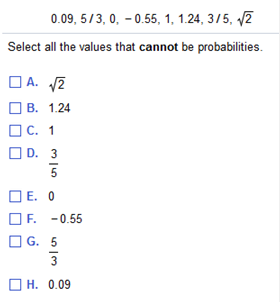 Answer:  Probability value should be between 0 to 1 (both inclusive) Probability shouldn't be a negative value Probability shouldn't be a value greater than 1. For a certain casino slot machine, the odds in favor of a win are given as 41 to 59. Express the indicated degree of likelihood as a probability value between 0 and 1 inclusive. The probability is .41 (Round to two decimal places as needed.) You are certain to get a number or a face card when selecting cards from a shuffled deck. Express the indicated degree of likelihood as a probability value between 0 and 1 inclusive. The probability is 1. (Type an integer or a decimal.) As per the given data, getting a red or black card is a certain event Probability of a certain event is 1 Answer: Probability = 1 Refer to the sample data for pre-employment drug screening shown below. If one of the subjects is randomly selected, what is the probability that the test result is a false positive? Who would suffer from a false positive result? Why? Pre-Employment Drug Screening Results Positive test result Negative test result Drug Use Is Indicated Drug Use Is Not Indicated Subject Uses Drugs 39 13 Subject Is Not a Drug User 17 34 The probability of a false positive test result is 0.165. (Round to three decimal places as needed.) Solve: 39 + 13+ 17 + 34 = 103 17 / 103 = .165 Who would suffer from a false positive result? Why? The person tested would suffer because he or she would be suspected of using drugs when in reality he or she does not use drugs. Refer to the sample data for polygraph tests shown below. If one of the test subjects is randomly selected, what is the probability that the subject is not lying? Is the result close to the probability of 0.461 for a negative test result? Did the Subject Actually Lie? No (Did Not Lie) Yes (Lied) Positive test results 12 43 Negative test results 35 12 (Type an integer or decimal rounded to three decimal places as needed.) The probability that a randomly selected polygraph test subject was not lying is Solve Is the result close to the probability, rounded to three decimal places, of 0.461 for a negative test result? Yes, because there is less than a 0.050 absolute difference between the probability of a true response and the probability of a negative test result. In a genetics experiment on peas, one sample of offspring contained 450 green peas and 48 yellow peas. Based on those results, estimate the probability of getting an offspring pea that is green. Is the result reasonably close to the value of 3/4 that was expected? The probability of getting a green pea is approximately nothing .904. (Type an integer or decimal rounded to three decimal places as needed.) 450 / 450 + 48 = .904 Is this probability reasonably close to three fourths ? Choose the correct answer below. A. No , it is not reasonably close. B. Yes, it is reasonably close. In a survey of consumers aged 12 and older, respondents were asked how many cell phones were in use by the household. (No two respondents were from the same household.) Among the respondents, 216 answered "none," 285 said "one," 361 said "two," 145 said "three," and 130 responded with four or more. A survey respondent is selected at random. Find the probability that his/her household has four or more cell phones in use. Is it unlikely for a household to have four or more cell phones in use? Consider an event to be unlikely if its probability is less than or equal to 0.05. (Round to three decimal places as needed.) P (four or more cell phones) = 0.114 Solve: 216 + 285 + 361 + 145 + 130 = 1137 130 / 1137 = 0.114 Is it unlikely for a household to have four or more cell phones in use? A. Yes , because the probability of a respondent with four or more cell phones in use is less than or equal to 0.05. B. No , because the probability of a respondent with four or more cell phones in use is greater than 0.05. C. No , because the probability of a respondent with four or more cell phones in use is less than or equal to 0.05. D. Yes, because the probability of a respondent with four or more cell phones in use is greater than 0.05. Among 350 randomly selected drivers in the 20 minus 24 age bracket, 6 were in a car crash in the last year. If a driver in that age bracket is randomly selected, what is the approximate probability that he or she will be in a car crash during the next year? Is it unlikely for a driver in that age bracket to be involved in a car crash during a year? Is the resulting value high enough to be of concern to those in the 20 minus 24 age bracket? Consider an event to be "unlikely" if its probability is less than or equal to 0.05. (Type an integer or decimal rounded to the nearest thousandth as needed.) The probability that a randomly selected person in the 20 minus 24 age bracket will be in a car crash this year is approximately .017. 6 / 350 = 0.017 Would it be unlikely for a driver in that age bracket to be involved in a car crash this year? Yes Is the probability high enough to be of concern to those in the 16 minus 18 age bracket? No
To the right are the outcomes that are
possible when a couple has three children.
Assume that boys and girls are equally likely, so that the eight simple events are equally 1st 2nd 3rd boy boy boy boy boy girl boy girl boy boy girl girl girl boy boy girl boy girl girl girl boy girl girl girl Find the probability that when a couple has three children, there are exactly 3 boys Solve: 8 total ways 1 way with 1 boy 1/8 = 0.125 A modified roulette wheel has 44 slots. One slot is 0, another is 00, and the others are numbered 1 through 42, respectively. You are placing a bet that the outcome is an odd number (In roulette, 0 and 00 are neither odd nor even.) a. What is your probability of winning? (Type an integer or a simplified fraction.) The probability of winning is: 21/44 Solve: 42 / 2 = 21 / 44 b. What are the actual odds against winning? The actual odds against winning are: 23:21 Solve: 44 – 21 = 23 = 23:21 c. When you bet that the outcome is an even number, the payoff odds are 1:1. How much profit do you make if you bet $16 and win? If you win, the payoff is: d. How much profit should you make on the $16 bet if you could somehow convince the casino to change its payoff odds so that they are the same as the actual odds against winning? $17.52 (Round to the nearest cent as needed.) Solve: 23 x 16 / 21 = $17.52 The _______ for a procedure consists of all possible simple events or all outcomes that cannot be broken down any further. Sample Space Which of the following is NOT a principle of probability? Choose the correct answer below. A. All events are equally likely in any probability procedure. B. The probability of any event is between 0 and 1 inclusive. C. The probability of an event that is certain to occur is 1. D. The probability of an impossible event is 0. Which of the following is NOT a principle of probability? Choose the correct answer below. A. The probability of any event is between 0 and 1 inclusive. B. All events are equally likely in any probability procedure. C. The probability of an impossible event is 0. D. The probability of an event that is certain to occur is 1. Fill in the blank. P(A) The _______ event A occurring are the ratio ----- P(A) Actual odds in favor of When randomly selecting an adult, A denotes the event of selecting someone with blue eyes. What do P(A) and P(A) represent? P(A) represents the probability of selecting an adult with blue eyes. P(A) represents the probability of selecting an adult who does not have blue eyes.
A research center poll showed that 84%
of people believe that it is morally wrong to not report all income on tax
returns.
What is the probability that someone does not have this belief? (Type an integer or a decimal.) The probability that someone does not believe that it is morally wrong to not report all income on tax returns is 0.16 Solve: 1- 0.84 = 0.16 or 16% Find the indicated complement. A certain group of women has a 0.02% rate of red/green color blindness. If a woman is randomly selected, what is the probability that she does not have red/green color blindness? (Type an integer or a decimal. Do not round.) What is the probability that the woman selected does not have red/green color blindness? 0.9998 Solve: The decimal equivalent of 0.02% is 0.0002 1 – 0.0002 = .9998 Add restaurants B, C, and D. Divide this by the total. Use the data in the following table, which lists drive-thru order accuracy at popular fast food chains. Assume that orders are randomly selected from those included in the table. Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 325 267 250 130 Order Not Accurate 39 50 37 20 If one order is selected, find the probability of getting food that is not from Restaurant A. The probability of getting food that is not from Restaurant A is .674 (Round to three decimal places as needed.) Solve: 325 + 267 + 250 + 130 + 39 + 50 + 37 + 20 = 1,118 1 – (325 + 39) / 1118 = .674 Use the data in the following table, which lists drive-thru order accuracy at popular fast-food chains. Assume that orders are randomly selected from those included in the table. Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 330 271 246 146 Order Not Accurate 36 53 37 18 If one order is selected, find the probability of getting an order that is not accurate. The probability of getting an order that is not accurate is 0.127 (Round to three decimal places as needed.) Solve: 330 + 271 + 246 + 146 + 36 + 53 + 37 + 18 = 1137 36 + 53 + 37 + 18 = 144 144 / 1137 = .127 Use the data in the following table, which lists drive-thru order accuracy at popular fast food chains. Assume that orders are randomly selected from those included in the table. Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 333 272 232 146 Order Not Accurate 35 58 36 10 = 1122 If one order is selected, find the probability of getting an order that is not accurate or is from Restaurant C. Are the events of selecting an order that is not accurate and selecting an order from Restaurant C disjoint events? The probability of getting an order from Restaurant C or an order that is not accurate is .331 (Round to three decimal places as needed.) 232 + 36 / 1122 + 35 + 58 + 36 + 10 / 1122 – 36 / 1122 = .3306595365 Are the events of selecting an order from Restaurant C and selecting an inaccurate order disjoint events? The events are not disjoint because it is possible to receive an inaccurate order from Restaurant C. Use the data in the following table, which lists drive-thru order accuracy at popular fast food chains. Assume that orders are randomly selected from those included in the table. Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 314 276 247 141 = 978 Order Not Accurate 39 52 35 17 = 1121 158 If two orders are selected, find the probability that they are both from Restaurant D. a. Assume that the selections are made with replacement. Are the events independent? b. Assume that the selections are made without replacement. Are the events independent? a. Assume that the selections are made with replacement. Are the events independent? The probability of getting two orders from Restaurant D is .0199 The events are independent because choosing the first order does not the choice of the second order. (Round to four decimal places as needed.) 158 / 1121 x 158 / 1121 = .0198656577 b. Assume that the selections are made without replacement. Are the events independent? The probability of getting two orders from Restaurant D is .0198. The events are not independent because choosing the first order affects the choice of the second order. (Round to four decimal places as needed.) 158 / 1121 x 157 / 1120 = .0197575507 Use the data in the following table, which lists drive-thru order accuracy at popular fast food chains. Assume that orders are randomly selected from those included in the table. Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 337 261 237 127 = 962 Order Not Accurate 37 50 39 14 = 1102 If two orders are selected, find the probability that they are both accurate. Complete parts (a) and (b) below. a. Assume that the selections are made with replacement. Are the events independent? The probability is .762. The events are independent. (Round to three decimal places as needed.) 962 / 1102 x 962 / 1102 = .7620561197 b. Assume that the selections are made without replacement. Are the events independent? The probability is .762 The events are not independent. (Round to three decimal places as needed.) 962 / 1102 x 961 / 1101 = .7619553912 Use the data in the following table, which lists drive-thru order accuracy at popular fast food chains. Assume that orders are randomly selected from those included in the table. Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 337 272 236 143 Order Not Accurate 34 52 39 12 total = 1125 371 155 If one order is selected, find the probability of getting an order from restaurant Upper A or Upper D or an order that is not accurate. or an order that is not accurate is 0.548 (Round to three decimal places as needed.) 371 + 155 + 52 + 39 / 1125 = 0.5484444444 Use the data in the following table, which lists drive-thru order accuracy at popular fast food chains. Assume that orders are randomly selected from those included in the table. Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 316 269 243 127 = 955 Order Not Accurate 30 58 38 17 281 Total = 1098 If three different orders are selected, find the probability that they are all from restaurant Upper C. The probability is .0168. (Round to four decimal places as needed.) 281 / 10983 = .1067614636 Use the following results from a test for marijuana use, which is provided by a certain drug testing company. Among 146 subjects with positive test results, there are 29 false positive results. Among 153 negative results, there are 3 false negative results. Complete parts (a) through (c). (Hint: Construct a table.) Positive Negative Use Marijuana 146 3 Not Use Marijuana 153 29 How many subjects were included in the study? The total number of subjects in the study was 299 146 + 153 = 299 How many subjects did not use marijuana? A total of 179 subjects did not use marijuana. 29 + 153 – 3 = 179 c. What is the probability that a randomly selected subject did not use marijuana? The probability that a randomly selected subject did not use marijuana is .599 (Do not round until the final answer. Then round to three decimal places as needed.) 179 / 299 = .5986622074 When using the _______ always be careful to avoid double-counting outcomes. Addition rule Events that are ____ cannot occur at the same time. Disjoint Complete the following statement. P (A or B) indicates _______. Choose the correct answer below. A. the probability that event A occurs in one trial followed by event B in another trial. B. the probability that A and B both occur in the same trial. C. the probability that in a single trial, event A occurs, event B occurs, or they both occur. D. the probability that event A or event B does not occur in a single trial. The table below shows the number of male and female students enrolled in nursing at a university for a certain semester. A student is selected at random. Complete parts (a) through (d). Nursing majors Non nursing majors Total Males 96 1011 1107 Females 600 1722 2322 Total 696 2733 3429 (a) Find the probability that the student is male or a nursing major. P(being male or being nursing major)equals 0.498 (Round to the nearest thousandth as needed.) 1107 + 696 – 96 = .4978127734 (b) Find the probability that the student is female or not a nursing major. P(being female or not being a nursing major)equals 0.972 (Round to the nearest thousandth as needed. 2322 + 2733 – 1722 / 3429 = .97220034996 (c) Find the probability that the student is not female or a nursing major. P(not being female or being a nursing major) = 0.498 (Round to the nearest thousandth as needed.) 1107 + 696 – 96 = .4978127734 (d) Are the events "being male" and "being a nursing major" mutually exclusive? Explain. A. No, because one can't be male and a nursing major at the same time. B. Yes, because one can't be male and a nursing major at the same time. C. No, because there are 96 males majoring in nursing. D. Yes, because there are 96 males majoring in nursing. The table below summarizes results from a study of people who refused to answer survey questions. A pharmaceutical company is interested in opinions of the elderly. What is the probability that the selected subject is someone 60 and over who responded? Age Age Responded Refused 18-21 76 11 22-29 258 20 30-39 248 33 40-49 139 26 50-59 141 35 60+ 205 57 = 1249 probability that the selected subject is someone 60 and over who responded = 0.164 (Round to three decimal places as needed.) 205 / 1249 = .164131305 The table below summarizes results from a study of people who refused to answer survey questions. A market researcher is interested in responses, especially from those between the ages of 22 and 39. Find the probability that a selected subject responds or is between the ages of 22 and 39 18-21 22-29 30-39 40-49 50-59 60+ Responded 76 258 248 139 141 205 Refused 10 19 32 25 34 56 The probability that the subject responded or is between the ages of 22 and 39 = 0.899 (Round to three decimal places as needed.) 76 + 258 + 248 + 139 + 141 + 205 + 10 + 19 + 32 + 25 + 34 + 56 = 1243 22 + 39 = 76 + 258 + 248 + 139 + 141 + 205 + 19 + 32 = 1118 1118 / 1243 = 0.899 Which word is associated with multiplication when computing probabilities? Choose the correct answer below. Not Disjoint Or And What does P(B|A) represent? Choose the correct answer below. A. The probability of event A and event B both occurring. B. The probability of event A or event B or both occurring. C. The probability of event B occurring after it is assumed that event A has already occurred. D. The probability of event A occurring after it is assumed that event B has already occurred. Fill in the blank. Two events A and B are _______ if the occurrence of one does not affect the probability of the occurrence of the other. Independent Fill in the blank. Selections made with replacement are considered to be _______. Independent Assuming boys and girls are equally likely, find the probability of a couple having a baby girl when their fourth child is born, given that the first three children were all girls. The probability is 0.5 (Type an integer or a simplified fraction.) Find the Complement first. Then use P( at least one) = 1 - P(complement) raised to ( how many , sample size) In a certain country, the true probability of a baby being a girl is 0.483. Among the next six randomly selected births in the country, what is the probability that at least one of them is a boy ? The probability is 0.987 (Round to three decimal places as needed.) 1 - .4836 = .987303536 In a certain country, the true probability of a baby being a boy is 0.526 Among the next five randomly selected births in the country, what is the probability that at least one of them is a girl? The probability is 0.960 (Round to three decimal places as needed.) 1 - .5265 = 9597349057 In an experiment, college students were given either four quarters or a $1 bill and they could either keep the money or spend it on gum. The results are summarized in the table. Complete parts (a) through (c) below. Purchased Gum Kept the Money Students Given Four Quarters 32 15 = 47 Students Given a $1 Bill 17 27 = 44 Total = 91 a Find the probability of randomly selecting a student who spent the money, given that the student was given four quarters. The probability is 0.681 (Round to three decimal places as needed.) 32 / 47 = .6808510638 b. Find the probability of randomly selecting a student who kept the money, given that the student was given four quarters. The probability is .319 (Round to three decimal places as needed.) 15 / 47 = .3191489362 c. What do the preceding results suggest? A. A student given four quarters is more likely to have kept the money than a student given a $1 bill. B. A student given four quarters is more likely to have spent the money than a student given a $1 bill. C. A student given four quarters is more likely to have spent the money. D. A student given four quarters is more likely to have kept the money. In an experiment, college students were given either four quarters or a $1 bill and they could either keep the money or spend it on gum. The results are summarized in the table. Complete parts (a) through (c) below. Purchased Gum Kept the Money Students Given Four Quarters 26 11 = 37 Students Given a $1 Bill 12 28 = 40 Total = 77 a Find the probability of randomly selecting a student who spent the money, given that the student was given a $1 bill. The probability is 0.300 (Round to three decimal places as needed.) 12 / 40 = .300 b. Find the probability of randomly selecting a student who kept the money, given that the student was given a $1 bill. The probability is 0.700 (Round to three decimal places as needed.) 28 / 40 = .700 c. What do the preceding results suggest? A. A student given a $1 bill is more likely to have spent the money. B. A student given a $1 bill is more likely to have kept the money than a student given four quarters. C. A student given a $1 bill is more likely to have kept the money. D. A student given a $1 bill is more likely to have spent the money than a student given four quarters. In an experiment, college students were given either four quarters or a $1 bill and they could either keep the money or spend it on gum. The results are summarized in the table. Complete parts (a) through (c) below. Purchased Gum Kept the Money Students Given Four Quarters 29 12 = 41 Students Given a $1 Bill 13 33 = 46 total = 87 a. Find the probability of randomly selecting a student who spent the money, given that the student was given four quarters. The probability is 0.707 (Round to three decimal places as needed.) 29 / 41 = .707 b. Find the probability of randomly selecting a student who spent the money, given that the student was given a $1 bill. The probability is 0.283 (Round to three decimal places as needed.) 13 / 33 = .28260 c. What do the preceding results suggest? A. A student given four quarters is more likely to have spent the money than a student given a $1 bill. B. A student was more likely to be given four quarters than a $1 bill. C. A student given a $1 bill is more likely to have spent the money than a student given four quarters. D. A student was more likely to have spent the money than to have kept the money. The data represent the results for a test for a certain disease. Assume one individual from the group is randomly selected. Find the probability of getting someone who tests positive, given that he or she had the disease. Yes No Positive 137 5 Negative 24 134 161 The probability is approximately .851 (Round to three decimal places as needed.) 137 / 161 = .850931677 The accompanying table shows the results from a test for a certain disease. Find the probability of selecting a subject with a negative test result, given that the subject has the disease. What would be an unfavorable consequence of this error? Yes No Positive 327 9 = 336 Negative 17 1124 = 1141 344 1131 total = 2954 The probability is 0.049 (Round to three decimal places as needed.) 17 / (17 + 327) = .0494186047 What would be an unfavorable consequence of this error? The subject would not receive treatment and could spread the disease.
The table below displays results from
experiments with polygraph instruments.
Find the positive predictive value for the test. That is, find the probability that the subject lied, given that the test yields a positive result. No (Did_Not_Lie) Yes (Lied) Positive test results 19 42 = 61 Negative test results 35 10 = 45 54 52 total = 106 The probability is 0.689 (Round to three decimal places as needed.) 42 / 61 = .6885245902 Complete the following statement. The conditional probability of B given A can be found by _______. Choose the correct answer below. A. assuming that event A has occurred, and then calculating the probability that event B will occur B. adding P(A) and P(B) C. multiplying P(A) times P(B) D. assuming that event B has occurred, and then calculating the probability that event A will occur A thief steals an ATM card and must randomly guess the correct threethree-digit pin code from a 77-key keypad. Repetition of digits is allowed. What is the probability of a correct guess on the first try? The number of possible codes is 343 (Type an integer or fraction. Simplify your answer.) 7 x 7 x 7 (7^3) = 343 The probability that the correct code is given on the first try is 1/343 (Type an integer or fraction. Simplify your answer.) 1 / 7 x 7 x 7 = 1/343
If you know the names of the remaining
three students in the spelling bee, what is the probability of
randomly selecting an order and getting the order that is used in the spelling bee? P(selecting the correct spelling bee order) = 1/6 (Type an integer or a simplified fraction.) 3 x 2 = 6
When testing for current in a cable
with seven color-coded wires, the author used a meter to test three wires at a
time.
How many different tests are required for every possible pairing of three wires? The number of tests required is 35 TI84 Plus 7! / (3! (7 - 3)!) = 35 Or 7 | MATH | PRB | nCr | 3 = 35
In a small private school, 5 students
are randomly selected from 11 available students.
What is the probability that they are the five youngest students? The probability is 1/462 (Type an integer or a simplified fraction.) 11! / 5! (11 – 5)!) = 462 = 1 / 462 Google it and use TI84 to check TI84 Plus ! = MATH | PRB Winning the jackpot in a particular lottery requires that you select the correct three numbers between 1 and 46 and, in a separate drawing, you must also select the correct single number between 1 and 31 Find the probability of winning the jackpot. The probability of winning the jackpot is 1 / 470580 (Type an integer or simplified fraction.) TI84 plus 46 | MATH | PRB | nCr | 3 = 15180 x 31 = 470580 = 1/470580 With a short time remaining in the day, a delivery driver has time to make deliveries at 6 locations among the 7 locations remaining. How many different routes are possible? There are 5040 possible different routes. (Simplify your answer.) TI84 plus 7 | MATH | PRB | nPr | 6 = 5040 A corporation must appoint a president, chief executive officer (CEO), chief operating officer (COO), and chief financial officer (CFO). It must also appoint a planning committee with three different members. There are 13 qualified candidates, and officers can also serve on the committee. Complete parts (a) through (c) below. How many different ways can the officers be appointed? There are 17160 different ways to appoint the officers. 13 MATH then PRB then nPr then 4 = 17160 Note: 4 = president chief executive officer (CEO) chief operating officer (COO) chief financial officer (CFO) How many difference ways to appoint to the committee? There are 286 ways to appoint to the committee? TI84 plus 13 | MATH | PRB | nCr | 3 = 286 Probability of getting the three youngest of the qualified members 1/286 When six basketball players are about to have a free-throw competition, they often draw names out of a hat to randomly select the order in which they shoot. What is the probability that they shoot free throws in alphabetical order? Assume each player has a different name. P(shoot free throws in alphabetical order) = 1 / 720 (Type an integer or a simplified fraction.) 6! = 720 = 1 / 720 (6 x 5 x 4 x 3 x 2 x 1) A clinical test on humans of a new drug is normally done in three phases. Phase I is conducted with a relatively small number of healthy volunteers. For example, a phase I test of a specific drug involved only 6 subjects. Assume that we want to treat 6 healthy humans with this new drug and we have 11 suitable volunteers available. Complete parts (a) through (c) below. If the subjects are selected and treated in sequence, so that the trial is discontinued if anyone displays adverse effects, how many different sequential arrangements are possible if 6 people are selected from the 11 that are available? Choose the correct answer below. A. 720 B. 462 C. 332640 D. 39800 Solution TI-84 PLUS 11 | MATH | PRB | nPr | 6 | ENTER 11 nPr 6 = 332640 If 6 subjects are selected from the 11 that are available, and the 6 selected subjects are all treated at the same time, how many different treatment groups are possible 462 11 nCr 6 = 462 Solution TI-84 PLUS 11 | MATH | PRB | nCr | 6 | ENTER c. If 6 subjects are randomly selected and treated at the same time, what is the probability of selecting the 6 youngest subjects? P (selecting the 6 youngest subjects) = 1 / 462 (Type an integer or a simplified fraction.) Which of the following is NOT a requirement of the Permutations Rule nPr = N! / N!-Nr for items that are all different? Choose the correct answer below. A. There are n different items available. B. Order is not taken into account (rearrangements of the same items are considered to be the same). C. Order is taken into account (rearrangements of the same items are considered to be different). D. Exactly r of the n items are selected (without replacement). Which of the following is NOT a requirement of the Combinations Rule nCr = N! / r!(n!-r)! for items that are all different?' Choose the correct answer below. A. That order is taken into account (consider rearrangements of the same items to be different sequences). B. That r of the n items are selected (without replacement). C. That order is not taken into account (consider rearrangements of the same items to be the same). D. That there be n different items available. Fill in the blank. If the order of the items selected matters, then we have a _______. Permutation problem A(n) __ is an ordered arrangement of r objects chosen from n distinct objects without repetition permutation
Suppose 46 cars start at a car race. In how
many ways can the top 3 cars finish the race?
The number of different top three finishes possible for this race of 46 cars is 91080 (Use integers for any number in the expression.) 46 nPr 3 = 91080 TI84 Plus 46 | MATH | PRB | nPr | 3 | ENTER Four members from a 24 -person committee are to be selected randomly to serve as 1 – 4 chairperson, vice-chairperson, secretary, and treasurer. The first person selected is the chairperson; the second, the vice-chairperson; the third, the secretary; and the fourth, the treasurer. There are 255024 possible different leadership structures. (Type an integer or fraction. Simplify your answer.) 24 nPr 4 = 255024 TI84 Plus 24 | MATH | PRB | nPr | 4 | ENTER
The
order does not matter. You must use combination here. nCr
To find the probability = 1 / answer from part b.
There is no part a. A corporation must appoint a planning committee with three different members. There are 14 qualified candidates, and officers can also serve on the committee. b. How many different ways can the committee be appointed? There are 364 different ways to appoint the committee. 14 nCr 3 = 364 TI84 Plus 14 | MATH | PRB | nCr | 3 | ENTER c. What is the probability of randomly selecting the committee members and getting the three youngest of the qualified candidates? P (getting the three youngest of the qualified candidates) = 1 / 364 (Type an integer or a simplified fraction.) A presidential candidate plans to begin her campaign by visiting the capitals in 3 of 46 states. What is the probability that she selects the route of three specific capitals? P (she selects the route of three specific capitals) = 1 / 91080 (Type an integer or a simplified fraction.) TI84 Plus 1 | MATH | PRB | nPr | 46 | ENTER When testing for current in a cable with twelve color-coded wires, the author used a meter to test five wires at a time. How many different tests are required for every possible pairing of five wires? The number of tests required is = 792 TI84 Plus 12 | MATH | PRB | nCr | 5 | ENTER In a small private school, 6 students are randomly selected from 18 available students. What is the probability that they are the six youngest students? The probability is 1 / 18564 (Type an integer or a simplified fraction.) TI84 Plus 1 | MATH | PRB | nCr | 18 | ENTER
With a short time remaining in the
day, a delivery driver has time to make deliveries at 7 locations among the
9 locations remaining. How many different routes are possible? There are 181440 possible different routes. (Simplify your answer.) TI84 Plus 9 | MATH | PRB | nPr | 7 | ENTER A corporation must appoint a president, chief executive officer (CEO), chief operating officer (COO), and chief financial officer (CFO). It must also appoint a planning committee with five different members. There are 15 qualified candidates, and officers can also serve on the committee. Complete parts (a) through (c) below. How many different ways can the officers be appointed? There are 32760 different ways to appoint the officers. TI84 Plus 15 | MATH | PRB | nPr | 4 | ENTER How many different ways to appoint to the committee? There are 3003 ways to appoint to the committee. TI 84 Plus 15 | MATH | PRB | nCr | 5 | ENTER c. What is the probability of randomly selecting the committee members and getting the five youngest of the qualified candidates? P (getting the five youngest of the qualified candidates) = 1 / 3003 (Type an integer or a simplified fraction.) Four of the 100 digital video recorders (DVRs) in an inventory are known to be defective. What is the probability that a randomly selected item is defective? The probability is 0.04 (Type an integer or a decimal. Do not round.) 4/100 = .04 In a test of a gender-selection technique, results consisted of 241 baby girls and 20 baby boys. Based on this result, what is the probability of a girl born to a couple using this technique? Does it appear that the technique is effective in increasing the likelihood that a baby will be a girl? The probability that a girl will be born using this technique is approximately 0.931 (Type an integer or decimal rounded to three decimal places as needed.) 217 / 271 + 20 = .9312714777 Does the technique appear effective in improving the likelihood of having a girl baby? Yes Find the indicated complement. A certain group of women has a 0.93 % rate of red/green color blindness. If a woman is randomly selected, what is the probability that she does not have red/green color blindness? What is the probability that the woman selected does not have red/green color blindness? 0.9907 (Type an integer or a decimal. Do not round.) 1 - .0093= .9907 Use the data in the following table, which lists drive-thru order accuracy at popular fast food chains. Assume that orders are randomly selected from those included in the table. Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 322 276 237 134 Order Not Accurate 31 56 37 11 If one order is selected, find the probability of getting an order from Restaurant A or an order that is accurate. Are the events of selecting an order from Restaurant A and selecting an accurate order disjoint events? The probability of getting an order from Restaurant A or an order that is accurate is: (Round to three decimal places as needed. 0.1104 322 + 276 + 237 + 134 + 31 = .1104 The principle of redundancy is used when system reliability is improved through redundant or backup components. Assume that a student's alarm clock has a 17.4% daily failure rate. Complete parts (a) through (d) below. a) What is the probability that the student's alarm clock will not work on the morning of an important final exam? 0.174 (Round to three decimal places as needed.) 17.4 / 100 = .174 b. If the student has two such alarm clocks, what is the probability that they both fail on the morning of an important final exam? 0.03027 (Round to five decimal places as needed.) .174 x .174 = .030276 c. What is the probability of not being awakened if the student uses three independent alarm clocks? 0.00527 (Round to five decimal places as needed.) .174 x .174 x .174 = .005268024 d. Do the second and third alarm clocks result in greatly improved reliability? A. Yes, because total malfunction would not be impossible, but it would be unlikely. B. No, because total malfunction would still not be unlikely. C. Yes, because you can always be certain that at least one alarm clock will work. D. No, because the malfunction of both is equally or more likely than the malfunction of one. Find the probability that when a couple has six children, at least one of them is a girl. (Assume that boys and girls are equally likely.) The probability is 63/64 that at least one of the six children is a girl . (Simplify your answer. Do not round.) 1 - (1/2)6 1 - 1/64 = 0.984375 63 / 64 Assuming boys and girls are equally likely, find the probability of a couple having a baby boy when their sixth child is born, given that the first five children were all boys. (Type an integer or a simplified fraction.) The probability is 1/2 At least one" is equivalent to _______. one or more At least one" corresponds to the values 1, 2, 3, and so on. Thus, "At least one" is equivalent to "one or more".
The order is important. Use the
graphing calculator. Use Permutation: nPr
There are 55 runners in a race. How many ways can the runners finish first, second, and third? There are 157,410 different ways that the runners can finish first through third (Type a whole number.) 55 nPr 3 = 157,410 Solve: TI84 Plus 55 MATH PRB nPr 3 ENTER How many different ways can the letters of "committee " be arranged? The number of different ways that the letters of "committee " can be arranged is 45,360 (Simplify your answer.) 9! / 8 = 9! = 45,360 Solve: TI84 Plus 9 MATH PRB ! ÷ 8 ENTER |
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |