|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Elementary Statistics Homework 1 2 3 4
5-6 6.3-7
8-10 | Tests Chapter 1-3
4 5-6 6.3-7 8-10 Final Review
Elementary Statistics
(STA2023)
Homework 3 Homework
3.1
Find the (a) mean, (b) median, (c) mode, and (d) midrange for the data and then (e) answer the given question. Listed below are the jersey numbers of 11 players randomly selected from the roster of a championship sports team. What do the results tell us? 64, 8, 68, 52, 45, 82, 85, 50, 94, 39, 70 a. Find the mean (Type an integer or a decimal rounded to one decimal place as needed.) The mean is 59.7. *Explanation: See TI84 Plus Instructions below! Or https://www.calculator.net/mean-median-mode-range-calculator.html b. Find the median. (Type an integer or a decimal rounded to one decimal place as needed.) The median is 64 *Explanation: To find the Median, arrange the numbers in descending order. The middle number is the median. c. Find the mode. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. The Mode is none. There is no mode. *Explanation: The Mode is the number that appears more than once. If there are two, put both. If not, the answer is NONE. d. Find the midrange. The midrange = 51 *Explanation: The Midrange is the greatest number value + the lowest value number ÷ 2. e. What do the results tell us? A. The midrange gives the average (or typical) jersey number, while the mean and median give two different interpretations of the spread of possible jersey numbers. B. Since only 11 of the jersey numbers were in the sample, the statistics cannot give any meaningful results. C. The mean and median give two different interpretations of the average (or typical) jersey number, while the midrange shows the spread of possible jersey numbers. D. The jersey numbers are nominal data and they do not measure or count anything, so the resulting statistics are meaningless. 64, 8, 68, 52, 45, 82, 85, 50, 94, 39, 70
Find
the (a) mean, (b) median, (c) mode, and (d) midrange for the data and
then (e) answer the given question.
Listed below are the weights in pounds of 11 players randomly selected from the roster of a championship sports team. Are the results likely to be representative of all players in that sport's league? 299, 219, 204, 229, 275, 223, 267, 257, 299, 237, 267 a. Find the mean. The mean is 252.4. *Explanation: See TI84 Plus Instructions below! Or https://www.calculator.net/mean-median-mode-range-calculator.html b. Find the median. The median is 257 pound(s). *Explanation: To find the Median, arrange the numbers in descending order. Out of numbers the middle number is the median. c. Find the mode. (Do not round. Use a comma to separate answers as needed.) The mode(s) is(are) 299, 267 pound(s). There is no mode. The Mode is the number that appears more than once. If there are two, put both. If not, the answer is NONE. d. Find the midrange. The midrange is 251.5 pound(s). The Midrange is the greatest number value + the lowest value number ÷ 2. e. Are the results likely to be representative of all players in that sport's league? A. The results are likely to be representative because a championship team is most likely representative of the entire league. B. The results are not likely to be representative because the median is not equal to the mean. C. The results are not likely to be representative because the median is not equal to the mode. D. The results are not likely to be representative because the championship team may not be representative of the entire league. 299, 219, 204, 229, 275, 223, 267, 257, 299, 237, 267
Listed below are selling prices (dollars) of TVs that are 60 inches or larger and rated as a "best buy" by a popular magazine. Are the resulting statistics representative of the population of all TVs that are 60 inches and larger? If you decide to buy one of these TVs, what statistic is most relevant, other than the measures of central tendency? 1950, 1100, 1400, 1100, 1800, 1200, 1100, 1150, 1200, 1000, 1100, 1450 a. Find the mean. (Type an integer or a decimal rounded to one decimal place as needed.) The mean is 1,295.8 See TI84 Plus Instructions below! Or https://www.calculator.net/mean-median-mode-range-calculator.html b. Find the median. (Type an integer or a decimal rounded to one decimal place as needed). The median is 1,175. To find the Median, arrange the numbers in descending order. Out of numbers the middle number is the median. c. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. (Type an integer or a decimal. Do not round. Use a comma to separate answers as needed.) The mode(s) is(are) 1,100. There is no mode. The Mode is the number that appears more than once. If there are two, put both. If not, the answer is NONE. d. Find the midrange. (Type an integer or a decimal rounded to one decimal place as needed.) The midrange is 1,475. The Midrange is the greatest number value + the lowest value number ÷ 2. e. Are the resulting statistics representative of the population of all TVs that are 60 inches and larger? Choose the best answer below. Since the sample is random and the sample size is greater than 10, the sample should not be considered to be representative of the population. The sample consists of the "best buy" TVs, so it is a random sample and is likely to be representative of the population. The sample consists of the "best buy" TVs, so it is not a random sample and is not likely to be representative of the population. Since the sample is random and the sample size is greater than 10, the sample can be considered to be representative of the population. If you decide to buy one of these TVs, what statistic is most relevant, other than the measures of central tendency? Choose the best answer below. The highest price is a relevant statistic for someone planning to buy one of the TVs. The price that occurs least frequently is a relevant statistic for someone planning to buy one of the TVs. The lowest price is a relevant statistic for someone planning to buy one of the TVs. The difference between the lowest price and the highest price is a relevant statistic for someone planning to buy one of the TVs. TI84 Plus Please note to find the mean from L1, you will need to remove L2 from the FreqList. Just to be sure, go to: STAT > CALC > 1-Var Stats and FreqList: should not have L2 to the right of it. If so, then select L2 And hit DEL to delete it. (To put it back, hit 2ND and the number 2). Should Look Like This 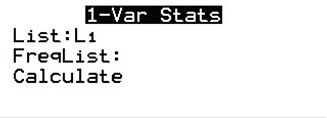 Solve: STAT > EDIT > LINE > L1 > ENTER DATA/NUMBERS in L1 > STAT > CALC > VAR STATS > CALCULATE.
Find
the (a) mean, (b) median, (c) mode, and (d) midrange for the data and
then (e) answer the given question.
Listed below are the amounts (dollars) it costs for marriage proposal packages at different sports venues. Are there any outliers? 49, 60, 60, 65, 65, 65, 75, 95, 100, 105, 150, 150, 225, 234, 275, 275, 350, 400, 425, 450, 450, 450, 450, 1500, 3000 a. Find the mean. Type an integer or a decimal rounded to two decimal places as needed.) The mean is 380.92 See TI84 Plus Instructions below! Or https://www.calculator.net/mean-median-mode-range-calculator.html b. Find the median. (Type an integer or a decimal rounded to two decimal places as needed.) The median is 225 To find the Median, arrange the numbers in descending order. Out of numbers the middle number is the median. c. Find the mode. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. (Type an integer or a decimal. Do not round. Use a comma to separate answers as needed.) There is no mode. The mode(s) is(are) 450 The Mode is the number that appears more than once. If there are two, put both. If not, the answer is NONE. d. Find the midrange. (Type an integer or a decimal rounded to two decimal places as needed.) The midrange is 1,524.5 The Midrange is the greatest number value + the lowest value number ÷ 2. e. Are there any outliers? Choose the correct answer below. The values $49, $1500, and $3000 appear to be outliers. The values $49 and $3000 appear to be outliers. The values $1500 and $3000 appear to be outliers. There do not appear to be any outliers. TI84 Plus Please note to find the mean from L1, you will need to remove L2 from the FreqList. Just to be sure, go to: STAT > CALC > 1-Var Stats and FreqList: should not have L2 to the right of it. If so, then select L2 And hit DEL to delete it. (To put it back, hit 2ND and the number 2). Should Look Like This  Solve: STAT > EDIT > LINE > L1 > ENTER DATA/NUMBERS in L1 > STAT > CALC > VAR STATS > CALCULATE.
Listed
below are pulse rates (beats per minute) from samples of adult males and
females.
Find the mean and median for each of the two samples and then compare the two sets of results. Does there appear to be a difference? Male: 54, 58, 61, 85, 56, 53, 62, 77, 52, 86, 60, 75, 64, 82, 64 Female: 84, 77, 90, 86, 89, 83, 93, 90, 91, 86, 72, 93, 82, 80, 87 Find the means. (Type integers or decimals rounded to one decimal place as needed.) The mean for males is 65.9 beats per minute and the mean for females is 85.5 beats per minute. The median for males is 62 beats per minute and the median for females is 86 beats per minute. (Type integers or decimals rounded to one decimal place as needed.) Compare the results. Choose the correct answer below. A. The mean and the median for males are both lower than the mean and the median for females. B. The median is lower for males, but the mean is lower for females. C. The mean and the median for females are both lower than the mean and the median for males. D. The mean and median appear to be roughly the same for both genders. E. The mean is lower for males, but the median is lower for females. Does there appear to be a difference? A. Since the sample size is small, no meaningful information can be gained from analyzing the data. B. The pulse rates for females appear to be higher than the pulse rates for males. C. There does not appear to be any difference. D. The pulse rates for males appear to be higher than the pulse rates for females. TI84 Plus Please note to find the mean from L1, you will need to remove L2 from the FreqList. Just to be sure, go to: STAT > CALC > 1-Var Stats and FreqList: should not have L2 to the right of it. If so, then select L2 And hit DEL to delete it. (To put it back, hit 2ND and the number 2). Should Look Like This  Solve: STAT > EDIT > LINE > L1 > ENTER DATA/NUMBERS in L1 > STAT > CALC > VAR STATS > CALCULATE.
Use
the magnitudes (Richter scale) of the earthquakes listed in the data set
below.
Find the mean and median of this data set. Is the magnitude of an earthquake measuring 7.0 on the Richter scale an outlier (data value that is very far away from the others) when considered in the context of the sample data given in this data set? Explain. 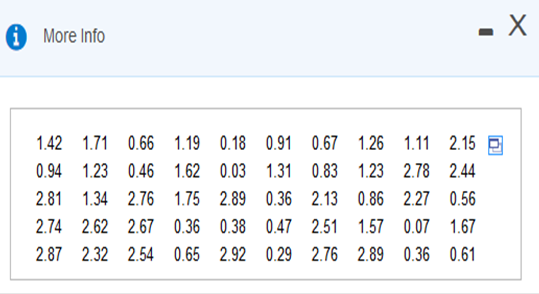 Find the mean and median of the data set using a calculator or similar data analysis technology. (Round to three decimal places as needed.) The mean of the data set is 1.503 The median of the data set is 1.325 Is the magnitude of an earthquake measuring 7.0 on the Richter scale an outlier when considered in the context of the sample data given? Yes, because this value is very far away from all of the other data values. No, because this value is not the maximum data value. No, because this value is not very far away from all of the other data values. Yes, because this value is the maximum data value. Please note to find the mean from L1, you will need to remove L2 from the FreqList. Just to be sure, go to: STAT > CALC > 1-Var Stats and FreqList: should not have L2 to the right of it. If so, then select L2 And hit DEL to delete it. (To put it back, hit 2ND and the number 2). Should Look Like This 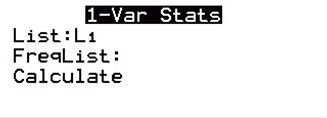 STAT > EDIT > LINE > L1 > ENTER DATA/NUMBERS in L1 > STAT > CALC > VAR STATS > CALCULATE.
Find
the mean of the data summarized in the given frequency distribution. Compare
the computed mean to the actual mean of 52.8
Low Temp (°F) Frequency 40-44 2 45-49 4 50-54 10 55-59 6 60-64 3 Which of the following best describes the relationship between the computed mean and the actual mean? A. The computed mean is close to the actual mean because the difference between the means is more than 5% of the actual mean. B. The computed mean is close to the actual mean because the difference between the means is less than 5% of the actual mean. C.The computed mean is not close to the actual mean because the difference between the means is less than 5% of the actual mean. D. The computed mean is not close to the actual mean because the difference between the means is more than 5% of the actual mean. TI84 Plus Please note to find the mean from L1, you will need to use L2 in the FreqList. Just to be sure, go to: STAT > CALC > 1-Var Stats and FreqList: hit 2ND and the number 2. Please note to find the mean from L1, you will need to use L2 in the FreqList. Just to be sure, go to: STAT > CALC > 1-Var Stats and FreqList: hit 2ND and the number 2. Should Look Like This  Solve: STAT > EDIT > LINE > L1 > ENTER DATA/NUMBERS in L1 & Frequency list in L2 Then > STAT > CALC > VAR STATS > CALCULATE.
Find
the mean of the data summarized in the given frequency distribution. Compare
the computed mean to the actual mean of 47.2 miles per hour.
Speed (mph) Frequency 42-45 25 46-49 15 50-53 7 54-57 3 58-61 1 (Round to the nearest tenth as needed.) The mean of the frequency distribution is 46.8 miles per hour. Which of the following best discribes the relationship between the computed mean and the actual mean? The computed mean is close to the actual mean because the difference between the means is more than 5%. The computed mean is not close to the actual mean because the difference between the means is more than 5%. The computed mean is close to the actual mean because the difference between the means is less than 5%. The computed mean is not close to the actual mean because the difference between the means is less than 5%. TI84 Plus Please note to find the mean from L1, you will need to use L2 in the FreqList. Just to be sure, go to: STAT > CALC > 1-Var Stats and FreqList: hit 2ND and the number 2. Should Look Like This  Solve: STAT > EDIT > LINE > L1 > ENTER DATA/NUMBERS in L1 & Frequency list in L2 Then > STAT > CALC > VAR STATS > CALCULATE.
A
student's course grade is based on one midterm that counts as
15% of his final grade, one class project that counts as 20% of his final grade, a set of homework assignments that counts as 35% of his final grade, and a final exam that counts as 30% of his final grade. His midterm score is 68, his project score is 80, his homework score is 79, his final exam score is 78. What is his overall final score? What letter grade did he earn (A, B, C, D, or F)? Assume that a mean of 90 or above is an A, a mean of at least 80 but less than 90 is a B, and so on His overall final score is 77.3 (Type an integer or a decimal rounded to one decimal place as needed.) His letter grade is a C 68 x 15 80 x 20 79 x 35 78 x 30 7725 / 100 = 77.25
Methods
used that summarize or describe characteristics of data are called _______
statistics
Descriptive
A
value at the center or middle of a data set is a(n) _______
A measure of center
Which
of the following is NOT a measure of center?
Census
The
measure of center that is the value that occurs with the greatest frequency
is the _______
Mode
Which
of the following is always true?
Choose the correct answer below. A. For skewed data, the mode is farther out in the longer tail than the median. B. The mean and median should be used to identify the shape of the distribution. C. Data skewed to the right have a longer left tail than right tail. D. In a symmetric and bell-shaped distribution, the mean, median, and mode are the same
The
brain volumes (cm^3) of 20 brains have a mean of 1169.5 cm^3 and a standard
deviation of 122.8 cm3. Use the given standard deviation and the range
rule of thumb to identify the limits separating values that are significantly
low or significantly high. For such data, would a brain volume of 1425.1
cm^3 be significantly high?
Significantly low values are 923.9 cm3 or lower. (Type an integer or a decimal. Do not round.) Is 1425.14 cm3 significantly high? Yes, since 1354.4 > 1314.4. Thus, correct option is: F. Yes, because it is above the upper limit separating value Solve: significantly low values are (< =) x – 2 x s 1169.6 – (2 x 122.8) = 923.9 significantly high values are (< =) x + 2 x s 1169.6 + (2 x 122.8) = 1415.1
A random sample of 10 subjects have
weights with a standard deviation of 12.0209
kg. What is the variance of their weights? Be sure to include the appropriate units with the result. (Round to four decimal places as needed.) The variance of the sample data is 144.5020 kg2 TI84 Plus Solve: 12.02092 (use the actual square root function not the preset)
Identify the symbols used for each
of the following:
(a) sample standard deviation; (b) population standard deviation; (c) sample variance; (d) population variance. a. The symbol for sample standard deviation is S b. The symbol for population standard deviation is o c. The symbol for sample variance is S2 d. The symbol for population variance is o2
Below are the jersey numbers of 11
players randomly selected from a football team. Find the range, variance,
and standard deviation for the given sample data. What do the results tell
us?
8 16 20 24 26 27 33 35 38 76 90 Range = 82 (Round to one decimal place as needed.) Solve: Subtract Maximum – Minimum 90 – 8 = 82 Sample standard deviation = 25.1 (Round to one decimal place as needed.) Please note to find the mean from L1, you will need to remove L2 from the FreqList. Just to be sure, go to: STAT > CALC > 1-Var Stats and FreqList: should not have L2 to the right of it. If so, then select L2 And hit DEL to delete it. (To put it back at a later time, hit 2ND and the number 2). Should Look Like This 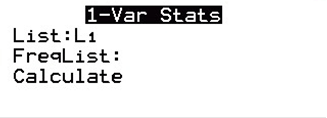 Solve: STAT > EDIT > LINE > L1 > ENTER DATA/NUMBERS in L1 > Then > STAT > CALC > VAR STATS > CALCULATE. Sx = standard deviation https://miniwebtool.com/sample-standard-deviation-calculator  Sample variance = 629.4 (Round to one decimal place as needed.) The Sample variance is the standard deviation2 (squared). There are two ways to compute the Sample variance. You can square the standard deviation manually (BEFORE it is rounded) or go back to STAT > CALC > VAR STATS > CALCULATE Then press VARS Statistics (5) Sx (3) square Sx > ^2. https://miniwebtool.com/variance-calculator/ What do the results tell us? A. Jersey numbers are nominal data that are just replacements for names, so the resulting statistics are meaningless. B. Jersey numbers on a football team vary much more than expected. C. The sample standard deviation is too large in comparison to the range. D. Jersey numbers on a football team do not vary as much as expected.
Listed below are the top 10 annual
salaries (in millions of dollars) of TV personalities. Find the range,
variance, and standard deviation for the sample data. Given that these are
the top 10 salaries, do we know anything about the variation of salaries of
TV personalities in general?
11.4 12.7 13 15 17 20 29 37 38 39 The range of the sample data is $27.6 million. (Type an integer or a decimal.) https://www.calculator.net/mean-median-mode-range-calculator.html The variance of the sample data is 129.13 (Round to two decimal places as needed.) https://miniwebtool.com/variance-calculator/ The standard deviation of the sample data is $11.36 million. (Round to two decimal places as needed.) https://miniwebtool.com/sample-standard-deviation-calculator/ Is the standard deviation of the sample a good estimate of the variation of salaries of TV personalities in general? A. No, because there is an outlier in the sample data. B. No, because the sample is not representative of the whole population. C. Yes, because the standard deviation is an unbiased estimator. D. Yes, because the sample is random. Listed below are the numbers of hurricanes that occurred in each year in a certain region. The data are listed in order by year. Find the range, variance, and standard deviation for the given sample data. Include appropriate units in the results. What important feature of the data is not revealed by any of the measures of variation? 1, 2, 3, 6, 7, 10, 14, 15, 16, 17, 17, 17, 18, 18 The range of the sample data is 17 hurricanes (Round to one decimal place as needed.) The standard deviation of the sample data is 6.4 hurricanes. (Round to one decimal place as needed.) https://miniwebtool.com/sample-standard-deviation-calculator/ The variance of the sample data is 41.5 hurricanes^2 (Round to one decimal place as needed.) https://miniwebtool.com/variance-calculator/ What important feature of the data is not revealed through the different measures of variation? A. The measures of variation reveal no information about the scale of the data. B. The measures of variation reveal nothing about how the numbers of hurricanes are spread. C. The measures of variation reveal nothing about the pattern over time. D. The measures of variation do not reveal the difference between the largest number of hurricanes and the smallest number of hurricanes in the data
Listed
below are measured amounts of caffeine (mg per
12oz of drink)
obtained in one can from each of 14 brands. Find the range,
variance, and standard deviation for the given sample data. Include
appropriate units in the results. Are the statistics representative of the
population of all cans of the same 14 brands
consumed?
0, 0, 0, 30, 31, 33, 33, 35, 45, 48, 50, 53, 53, 55 (Round to one decimal place as needed.) The range of the sample data is 55 mg per 12oz of drink. (Round to one decimal place as needed.) The standard deviation of the sample data is 20.0 mg per 12oz of drink. (Round to one decimal place as needed.) The variance of the sample data is 401.9 mg per 12oz of drink2 Are the statistics representative of the population of all cans of the same 14 brands consumed? The statistics are likely representative of the population of all cans of these brands that are consumed because the results from any sample of the 14 brands will be typical of the population. The statistics are not necessarily representative of the population of all cans of these brands that are consumed because each brand is weighted equally in the calculations. It is unlikely that each of the 14 brands of soda are consumed equally. The statistics are not necessarily representative of the population of all cans of these brands that are consumed because it is necessary to have at least 5 of each brand in order to get a sample that is representative of the population. The statistics are likely representative of the population of all cans of these brands that are consumed because each brand is being represented in the sample. Listed below are foot lengths in inches for 11 randomly selected people taken in 1988. Find the range, variance, and standard deviation for the given sample data. Include appropriate units in the results. Are the statistics representative of the current population of all people? 8.8, 8.9, 8.9, 8.9, 9.1, 9.3, 9.4, 10.1, 10.3, 10.3, 10.4 The range of the sample data is 1.6 inches (Type an integer or a decimal. Do not round.) https://www.calculator.net/mean-median-mode-range-calculator.html The standard deviation of the sample data is 0.65 inches (Round to two decimal places as needed.) https://miniwebtool.com/sample-standard-deviation-calculator/ The variance of the sample data is 0.422 inches (Round to two decimal places as needed.) https://miniwebtool.com/variance-calculator/ Are the statistics representative of the current population of all people? A. The statistics are representative because they are taken from a random sample. B. The statistics are representative because the standard deviation of the sample data is less than 1. C. Since the measurements were made in 1988, it is not necessarily representative of the population today. D. The statistics are not representative because a smaller sample is needed to represent the population. A certain group of test subjects had pulse rates with a mean of 75.7 beats per minute and a standard deviation of 12.7 beats per minute. Use the range rule of thumb to identify the limits separating values that are significantly low or significantly high. Is a pulse rate of 111.1 beats per minute significantly low or significantly high? significantly low values are 50.3 beats per minute or lower. (Type an integer or a decimal. Do not round.) 75.7 – (2 x 12.7) = 50.3 Significantly high values are 101.1 beats per minute or higher. (Type an integer or a decimal. Do not round.) 75.7 + (2 x 12.7) = 101.1 Is a pulse rate of 111.1 beats per minute significantly low or significantly high? A. Neither, because it is within two standard deviations of the mean. B. Significantly high, because it is greater than two standard deviations above the mean. C. Significantly low, because it is less than two standard deviations below the mean. D. It is impossible to determine with the information given
A group of adult males has foot
lengths with a mean of 26.72 cm and a standard deviation of 1.27 cm. Use the
range rule of thumb to identify the limits separating values that are
significantly low or significantly high. Is the adult male foot length of 29.7
cm significantly low or significantly high? Explain.
Significantly low values are 24.18 cm or lower. (Type an integer or a decimal. Do not round.) 26.72 – (1.27 x 2) = 24.18 Significantly high values are 29.26 cm or higher. (Type an integer or a decimal. Do not round.) 26.72 = (2 x 1.27) = 29.26 Select the correct choice below and fill in the answer box(es) to complete your choice. A. The adult male foot length of 29.7 cm is significantly high because it is greater than 29.26 cm. (Type an integer or a decimal. Do not round.) B. The adult male foot length of 29.7 cm is not significant because it is between ___ cm and nothing cm. (Type integers or decimals. Do not round.) C. The adult male foot length of 29.7 cm is significantly low because it is less than ___ cm. (Type an integer or a decimal. Do not round.) Find the standard deviation, s, of sample data summarized in the frequency distribution table below by using the formula below, where x represents the class midpoint, f represents the class frequency, and n represents the total number of sample values. Also, compare the computed standard deviation to the standard deviation obtained from the original list of data values, 11.1 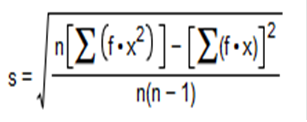 Interval Frequency 20-29 1 30-39 2 40-49 1 50-59 3 60-69 15 70-79 39 80-89 39 Standard Deviation equals 11.5 20 + 29 / 2 = 24.5 30 + 39 / 2 = 34.5 40 + 49 / 2 = 44.5 50 + 59 / 2 = 54.5 60 + 69 / 2 = 64.5 70 + 79 / 2 = 74.5 80 + 89 / 2 = 84.5 20 + 29 / 2 = 24.5 Interval Frequency 24.5 1 34.5 2 44.5 1 54.5 3 64.5 15 74.5 39 84.5 39 TI84 Plus Please note to find the mean from L1, you will need to use L2 in the FreqList. Just to be sure, go to: STAT > CALC > 1-Var Stats and FreqList: hit 2ND and the number 2. Should Look Like This  Steps to Solve: STAT EDIT L1 > ENTER DATA/NUMBERS in L1 Enter the Frequency list in > L2 STAT CALC VAR STATS CALCULATE Useful Tool https://www.hackmath.net/en/calculator/standard-deviation Consider a difference of 20% between two values of a standard deviation to be significant. How does this computed value compare with the given standard deviation, 11.1? The computed value is significantly less than the given value. The computed value is significantly less than the given value. The computed value is significantly greater than the given value. The computed value is significantly greater than the given value. The computed value is not significantly different from the given value. Find the standard deviation, s, of sample data summarized in the frequency distribution table given below by using the formula below, where x represents the class midpoint, f represents the class frequency, and n represents the total number of sample values. Also, compare the computed standard deviation to the standard deviation obtained from the original list of data values, 9.0. 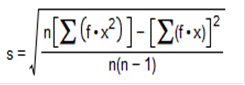 Interval Frequency 30-36 5 - 33 37-43 19 - 40 44-50 37 - 47 51-57 22 - 54 58-64 7 - 61 65-71 3 - 68 https://www.hackmath.net/en/calculator/standard-deviation Corrected sample standard deviation s = 7.7663700039853 Standard deviation is 7.8. Follow the same steps as above or use https://www.hackmath.net/en/calculator/standard-deviation (Round to one decimal place as needed.) Consider a difference of 20% between two values of a standard deviation to be significant. How does this computed value compare with the given standard deviation, 9.0? A. The computed value is not significantly different from the given value. B. The computed value is significantly less than the given value. C. The computed value is significantly greater than the given value. (All units are 1000 cells/muL.) Using the empirical rule, find each approximate percentage below. a. What is the approximate percentage of women with platelet counts within 1 standard deviation of the mean, or between 186.9 and 310.5? b. What is the approximate percentage of women with platelet counts between 125.1 and 372.3? a. Approximately 68% of women in this group have platelet counts within 1 standard deviation of the mean, or between 186.9 and 310.5. (Type an integer or a decimal. Do not round.) b. Approximately 95% of women in this group have platelet counts between 125.1 and 372.3. (Type an integer or a decimal. Do not round.)
The body temperatures of a group of
healthy adults have a bell-shaped distribution with a mean of
98.23 degrees Fand a standard deviation of 0.66 degrees F. Using the empirical rule, find each approximate percentage below. 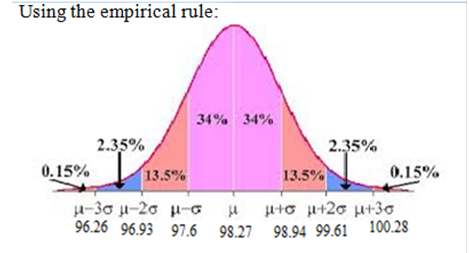 The empirical rule states that for data sets having a distribution that is approximately bell-shaped, the following properties apply. About 68% of all values fall within 1 standard deviation of the mean. About 95% of all values fall within 2 standard deviations of the mean. About 99.7% of all values fall within 3 standard deviations of the mean. a. What is the approximate percentage of healthy adults with body temperatures within 2 standard deviations of the mean, or between 96.91 degrees F and 99.55 degrees F? b. What is the approximate percentage of healthy adults with body temperatures between 97.57 degrees F and 98.89 degrees F? a. Approximately 95% of healthy adults in this group have body temperatures within 2 standard deviations of the mean, or between 96.91 degrees F and 99.55 degrees F. (Type an integer or a decimal. Do not round.) b. Approximately 68% of healthy adults in this group have body temperatures between 97.57 degrees F and 98.89 degrees F. (Type an integer or a decimal. Do not round.) If your score on your next statistics test is converted to a z score, which of these z scores would you prefer: - 2.00, -1.00, 0, 1.00, 2.00? Why? A. The z score of -2.00 is most preferable because it is 2.00 standard deviations below the mean and would correspond to the highest of the five different possible test scores. B. The z score of 1.00 is most preferable because it is 1.00 standard deviation above the mean and would correspond to an above average test score. C. The z score of -1.00 is most preferable because it is 1.00 standard deviation below the mean and would correspond to an above average test score. D. The z score of 0 is most preferable because it corresponds to a test score equal to the mean. E. The z score of 2.00 is most preferable because it is 2.00 standard deviations above the mean and would correspond to the highest of the five different possible test scores A Z-score (or standardized value) is the number of standard deviations that a given value x is above or below the mean. A negative z score corresponds to an x value less than the mean. A positive z score corresponds to an x value greater than the mean. The more negative the z score, the further the x value is below the mean. The more positive the z score, the further the x value is above the mean. Fill in the blank. When a data value is converted to a standardized scale representing the number of standard deviations the data value lies from the mean, we call the new value a _______ z-score Which of the following is NOT a value in the 5-number summary? Choose the correct answer below. Minimum Q1 Mean Median A successful basketball player has a height of 6 feet 11 inches, or 211 cm. Based on statistics from a data set, his height converts to the z score of 5.17. How many standard deviations is his height above the mean? The player's height is nothing standard deviation(s) 5.17 above the mean. (Round to two decimal places as needed.) The boxplot shown below results from the heights (cm) of males listed in a data set. What do the numbers in that boxplot tell us? 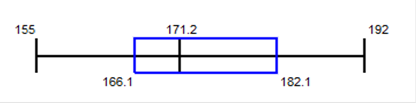 A boxplot consists of a box that extends from 166.1 to 182.1, a vertical line segment drawn through the box at 171.2, and a horizontal line segment extending from a vertical line segment at 155 to a vertical line segment at 192 that bisects the box. The minimum height is 155 cm. The first quartile Q1 is 166.1 cm. The second quartile Q2 (or the median) is 171.2 cm. The third quartile Q3 is 182.1 cm. and the maximum height is 192 cm. (Type integers or decimals. Do not round.) Instructors Tip a. The difference = highest rate - lowest rate b. answer from part a divided by s c. z = x (raw score) - mean/ s d. A z score between -2 and 2 is not significant. For a data set of the pulse rates for a sample of adult females, the lowest pulse rate is 39 beats per minute, the mean of the listed pulse rates is x overbar equals 73.0 beats per minute, and their standard deviation is equals 10.2 beats per minute. a. What is the difference between the pulse rate of 39 beats per minute and the mean pulse rate of the females? b. How many standard deviations is that [the difference found in part (a)]? c. Convert the pulse rate of 39 beats per minute to a z score. d. If we consider pulse rates that convert to z scores between minus 2 and 2 to be neither significantly low nor significantly high, is the pulse rate of 39 beats per minute significant? a. The difference is 34 beats per minute. (Type an integer or a decimal. Do not round.) 73 – 39 b. The difference is 3.33 standard deviations. (Round to two decimal places as needed.) 73 – 39 ÷ 10.2 c. The z score is z = -3.33 (Round to two decimal places as needed.) 39 – 73 ÷ 10.2 d. The lowest pulse rate is significantly low. Consider a value to be significantly low if its z score less than or equal to -2 or consider a value to be significantly high if its z score is greater than or equal to 2. A test is used to assess readiness for college. In a recent year, the mean test score was 21.8 and the standard deviation was 4.6. Identify the test scores that are significantly low or significantly high. What test scores are significantly low? Select the correct answer below and fill in the answer box(es) to complete your choice. A. Test scores that are between and. (Round to one decimal place as needed. Use ascending order.) B. Test scores that are greater than nothing. (Round to one decimal place as needed.) C. Test scores that are less than 12.6. (Round to one decimal place as needed.) Solve: -2 = 21.8 ÷ 4.6 -9.2 = 21.8 21.8 – 9.2 = 12.6 What test scores are significantly high? Select the correct answer below and fill in the answer box(es) to complete your choice. A. Test scores that are between nothing and (Round to one decimal place as needed. Use ascending order.) B. Test scores that are greater than 30.8 (Round to one decimal place as needed.) C. Test scores that are less than (Round to one decimal place as needed.) 2(4.5) = 21.8 = 30.8 Use z scores to compare the given values. The tallest living man at one time had a height of 230 cm. The shortest living man at that time had a height of 76.6 cm. Heights of men at that time had a mean of 173.84 cm and a standard deviation of 5.68 cm. Which of these two men had the height that was more extreme? Since the z score for the tallest man is z = 9.89 and the z score for the shortest man is z equals , the shortest man had the height that was more extreme. (Round to two decimal places.) Solve: 230 – 173.84 ÷ 5.68 = 9.89 76.6 – 173.84 ÷ 5.68 = 17.12 Use z scores to compare the given values. In a recent awards ceremony, the age of the winner for best actor was 31 and the age of the winner for best actress was 47. For all best actors, the mean age is 44.1 years, and the standard deviation is 8.2 years. For all best actresses, the mean age is 31.5 years, and the standard deviation is 12.8 years. (All ages are determined at the time of the awards ceremony.) Relative to their genders, who had the more extreme age when winning the award, the actor or the actress? Explain. Since the z score for the actor is z = -1.60 and the z score for the actress is z = 1.21 the actor had the more extreme age. (Round to two decimal places.) Solve: 31 – 44.1 ÷ 8.2 = -1.6 47 – 31.5 ÷ 12.8 = 1.21 Actor The following are the ratings of males by females in an experiment involving speed dating. Use the given data to construct a boxplot and identify the 5-number summary. 3 4 5 5 5 5 5.5 5.5 5.5 5.5 5.5 6.5 6.5 6.5 6.5 6.5 7.5 8.5 8.5 8.5 The 5-number summary is 3, 5 , 5.5 , 6.5, and 8.5. (Use ascending order. Type integers or decimals. Do not round.) Stat > Edit = Min, Q1, Med, Q3, and Max Which boxplot below represents the data? 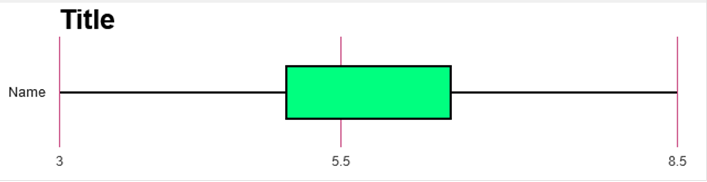 Useful Tool https://www.statskingdom.com/boxplot-maker.html Whenever a data value is less than the mean, _______. the corresponding z-score is negative. A frequency table of grades has five classes (A, B, C, D, F) with frequencies of 2, 10 ,13, 5, 2 respectively. Using percentages, what are the relative frequencies of the five classes? 2 10 13 5 2 Complete the table.  2 + 10 + 13 + 5 + 2 = 32 DIVIDE BY 32 x 100 32 x 100 Identify the lower class limits, upper class limits, class width, class midpoints, and class boundaries for the given frequency distribution. Also identify the number of individuals included in the summary. Age (yr) when award was won Frequency 25 to 34 27 35 to 44 35 45 to 54 12 55 to 64 3 65 to 74 4 75 to 84 1 85 to 94 1 Identify the lower-class limits. (Type integers or decimals. Do not round. Use ascending order.) 25,35,45,55,65,75,85 Identify the upper-class limits. (Type integers or decimals. Do not round. Use ascending order.) 34,44,54,64,74,84,94 Identify the class width. (Type integers or decimals. Do not round. Use ascending order.) 10 Identify the class midpoints. (Type integers or decimals. Do not round. Use ascending order.) 29.5,39.5,49.5,59.5,69.5,79.5,89.5 Identify the class boundaries. (Type integers or decimals. Do not round. Use ascending order.) 24.5,34.5,44.5,55.5,65.5,75.5,85.5,95.5 Identify the class boundaries. (Type integers or decimals. Do not round. Use ascending order.) 24.5,34.5,44.5,54.5,64.5,74.5,84.5,94.5 Identify the number of individuals included in the summary. 83 Identify the lower class limits, upper class limits, class width, class midpoints, and class boundaries for the given frequency distribution. Also identify the number of individuals included in the summary. Blood Platelet Count of Females Frequency 100 to 199 26 200 to 299 93 300 to 399 29 400 to 499 0 500 to 599 2 Identify the lower-class limits. (Type integers or decimals. Do not round. Use ascending order.) 100,200,300,400,500 Identify the upper-class limits. (Type integers or decimals. Do not round. Use ascending order.) 199 ,299,399,499,599 (Type integers or decimals. Do not round. Use ascending order.) Identify the class width. (Type integers or decimals. Do not round.) 100 Identify the class midpoints. (Type integers or decimals. Do not round. Use ascending order.) 149.5,249.5,349.5,449.5,549.5 Identify the class boundaries. (Type integers or decimals. Do not round. Use ascending order.) 99.5,199.5,299.5,399.5,499.5,599.5 Identify the number of individuals included in the summary. (Type a whole number.) 150
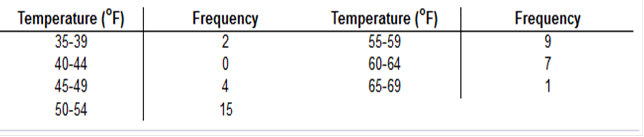
Does the
frequency distribution appear to have a normal distribution using a strict
interpretation of the relevant criteria?
 Does the frequency distribution appear to have a normal distribution? A. No, the frequencies do not decrease from the maximum frequency to a low frequency. B. No, the distribution does not appear to be normal. C. Yes, all the requirements are met. Among fatal plane crashes that occurred during the past 65 years, 227 were due to pilot error, 84 were due to other human error, 663 were due to weather, 470 were due to mechanical problems, and 107 were due to sabotage. Cause Frequency Pilot error 227 Other human error 84 Weather 663 Mechanical Problems 470 Sabotage 107 Construct the relative frequency distribution. What is the most serious threat to aviation safety, and can anything be done about it? Complete the relative frequency distribution below. Cause Relative Frequency Pilot error 14.6% Other human error 5.4% Weather 42.7% Mechanical problems 30.3% Sabotage 6.9% (Round to one decimal place as needed.) What is the most serious threat to aviation safety, and can anything be done about it?  Which characteristic of data is a measure of the amount that the data values vary? Choose the correct answer below. Center Variation Time Distribution A _______ helps us understand the nature of the distribution of a data set. Frequency distribution Class width is found by _______. Choose the correct answer below. A. subtracting a lower-class limit from the next consecutive lower class limit. B. adding the lower-class limit to the upper-class limit and dividing by two. C. subtracting the smallest value in the data set from the largest value in the data set. D. subtracting the lower limit of one class from the upper limit of that same class. Heights of adult males are normally distributed. If a large sample of heights of adult males is randomly selected and the heights are illustrated in a histogram, what is the shape of that histogram? Choose the correct answer below. Longer tail to the left Longer tail to the right Bell-shaped Uniform The histogram to the right represents the weights (in pounds) of members of a certain high-school debate team. How many team members are included in the histogram? 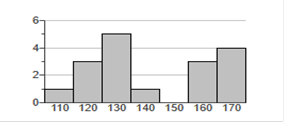 The histogram represents debate team, 17 members. Measure and add the lines on the graph. Example 110 would be 1 team member. 120 would be 3 team members, and so on. 1 + 3 + 5 + 1 + 3 + 4 = 17 The histogram to the right represents the weights (in pounds) of members of a certain high-school debate team. What is the class width? What are the approximate lower and upper class limits of the first class? 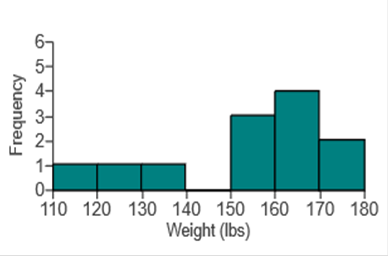 What is the class width? 10. What are the approximate lower and upper-class limits of the first class? The approximate lower-class limit is 110. The approximate upper-class limit is 120. The table below shows the frequency distribution of the rainfall on 52 consecutive Wednesdays in a certain city. Use the frequency distribution to construct a histogram. Do the data appear to have a distribution that is approximately normal 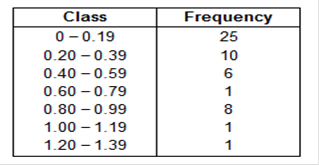 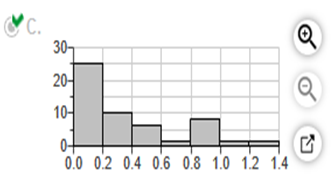 Do the data appear to have a distribution that is approximately normal? A. No, it is approximately uniform. B. Yes, it is approximately normal. C. No, it is not symmetric. D. No, it has no obvious maximum. Given below are the numbers of indoor movie theaters, listed in order by row for each year. Use the given data to construct a time-series graph. What is the trend? How does this trend compare to the trend for drive-in movie theaters? Year Number of Indoor Theaters 1 20595 2 20853 3 21907 4 22125 5 23740 6 25709 7 24789 8 27852 9 26995 10 29644 11 31050 12 30423 13 36448 14 33445 15 34490 16 37202 17 35361 A time-series graph titled "Number of Drive-in Movie Theaters" with horizontal axis. Construct a time-series graph with the year on the horizontal axis and the number of theaters on the vertical axis. 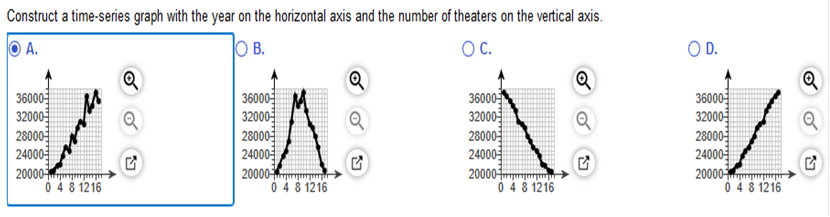 What is the trend? How does this trend compare to the trend for drive-in movie theaters? A. There appears to be a downward trend, similar to drive-in movie theaters, which also have a downward trend. B. There appears to be an upward then downward trend, unlike drive-in movie theaters, which only have a downward trend. C. There appears to be an upward trend, unlike drive-in movie theaters, which have a downward trend. Low (°F) Temperature Frequency 40-44 2 45-49 4 50-54 13 55-59 7 60-64 2 *Explanation Find the midpoints (Example 40 + 44 / 2 = 42) then the TI84 Plus as above. The mean of the frequency distribution is 52.5 degrees. (Round to the nearest tenth as needed.) Which of the following best describes the relationship between the computed mean and the actual mean? A. The computed mean is not close to the actual mean because the difference between the means is more than 5% of the actual mean. B. The computed mean is not close to the actual mean because the difference between the means is less than 5% of the actual mean. C. The computed mean is close to the actual mean because the difference between the means is less than 5% of the actual mean. D. The computed mean is close to the actual mean because the difference between the means is more than 5% of the actual mean. Use the range rule of thumb to estimate the standard deviations and compare the result to the exact standard deviation of 169.5 cm3, assuming the estimate is accurate if it is within 15 cm3. The estimated standard deviation is 141 cm3 (Type an integer or a decimal. Do not round.) *Explanation: 1495 – 932 / 4 = 141 Max / min rule is to divide by 4. Compare the result to the exact standard deviation. A. The approximation is not accurate because the error of the range rule of thumb's approximation is greater than 15 cm3. B. The approximation is accurate because the error of the range rule of thumb's approximation is greater than 15 cm cubed. C. The approximation is not accurate because the error of the range rule of thumb's approximation is less than 15 cm cubed. D. The approximation is accurate because the error of the range rule of thumb's approximation is less than 15 cm cubed. and the range rule of thumb to identify the limits separating values that are significantly low or significantly high. For such data, would a brain volume of 1433.8 cm^3 be significantly high? (Type an integer or a decimal. Do not round.) Significantly low values are 887.4 cm3 or lower. *Explanation: 1,135.6 – 2 x 124.1 = 887.4 Significantly high values are 1383.8 cm3 or higher. *Explanation: 1,135.6 + 2 x 124.1 = 1383.8 Is 1433.8 cm cubed significantly high? A. No, because it is below the lower limit separating value. B. No, because it is above the upper limit separating value. C. Yes comma because it is above the upper limit separating value. D. Yes comma because it is below the lower limit separating value. E. Yes, because it is between the limits separating values. F. No comma because it is between the limits separating values. Which measure of variation is most sensitive to extreme values range variance |
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |
