Elementary Statistics (STA2023)
Chapter Test 8 - 10

A data set includes data from 400 random tornadoes.
The display from technology available below results from using the tornado lengths (miles)
to test the claim that the mean tornado length is greater than 2.1 miles.
Use a 0.05 significance level. Identify the null and alternative hypotheses, test statistic, P-value,
and state the final conclusion that addresses the original claim.
 

 
H₀: μ = 2.1
H₁: μ > 2.1
 
Explanation:
This is given above!
 
Identify the test statistic.
2.35 (Round to two decimal places as needed.)
 
This is given above: T-Stat 2.353835 (round to two decimal places)
 
Identify the P-value.
.010 (Round to three decimal places as needed.)
 
This is given above: P-value 0.0095 (round to three decimal places)
 
Reject HO. There is sufficient evidence to support the claim that the mean tornado length is greater than 2.1 miles.

In a study of 785 randomly selected medical malpractice lawsuits, it was found that 512 of them were dropped or dismissed.
Use a 0.01 significance level to test the claim that most medical malpractice lawsuits are dropped or dismissed.
 
Part 1
H₀: p = 0.50
H₁: p ≠ 0.50
 
Part 2
What is the test statistic?
8.53
(Round to three decimal places as needed.)
Part 3
What is the conclusion about the null hypothesis?
 
Reject the null hypothesis because the P-value is greater than the significance level, a.
 
Explanation:
Part 1
H₀: p = 0.50
H₁: p ≠ 0.50
We are looking for this test statistic.

USE THE TI84 PLUS
STAT
TESTS
PropZTest: P: = .50 | x = 512 | n = 785 | ≠p (make sure ≠p is highlighted) | Calculate
z = 8.530275792 (round to 8.53)

*Note the PropZTest is 5:1 PropZTest.
 
Part 2
TI84 PLUS
2^nd | VARS
Normalcdf: -9999 / -8.53 / 0 / 1 = 0
Or
TI84 PLUS
2^nd | VARS
Normalcdf: -9999 / 8.53 / 0 / 1 = 1
P (z > 8.53) = 1 – P (z < 8.53) = 0
 
Part 3
Reject the null hypothesis because the P-value is greater than the significance level, a.
 
We would reject the null hypothesis since the P-Value of 0 is less than the 0.01 significance level.

Claim: Most adults would not erase all of their personal information online if they could. A software firm survey of 494
randomly selected adults showed that 41% of them would erase all of their personal information online if they could.
Complete parts​ (a) and​ (b) below.
a.      Express the original claim in symbolic form. Let the parameter represent the adults that would erase their personal information.
P < 0.50
Type an integer or a decimal. Do not​ round.)
 
b.      Identify the null and alternative hypothesis.
H₀: P = 0.50
H₁: P < 0.50
 

 
Which of the following statements about correlation is true?
Choose the correct answer below.
 
A.     We say that there is a positive correlation between x and y if the x-values increase as the corresponding y-values increase.
B.      We say that there is a negative correlation between x and y if the x-values increase as the corresponding y-values increase.
C.      We say that there is a positive correlation between x and y if there is no distinct pattern in the scatterplot_
D.     We say that there is a positive correlation between x and y if the x-values increase as the corresponding y-values decrease.
 

 
The table provided below shows paired data for the heights of a certain country’s presidents,
and their main opponents in the election campaign. Construct a scatterplot. Does there appear to be a correlation?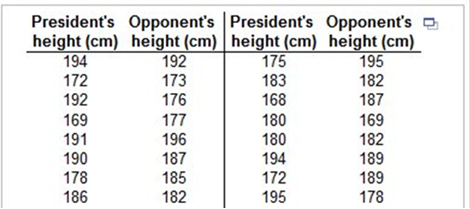
 

 
Choose the correct scatterplot below.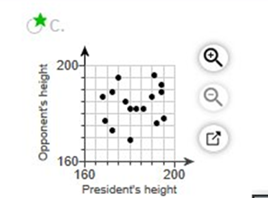

 
Does there appear to be a correlation between the president's height and his opponent's height?
 
A.      Yes, there appears to be a correlation. The candidate with the highest height usually wins.
B.      Yes, there appears to be a correlation. As the president's height increases, his opponent's height decreases.
C.      Yes, there appears to be a correlation. As the president's height increases, his opponent's height increases.
D.     No, there does not appear to be a correlation because there is no general pattern to the data.
 

Assume a significance level of a = 0.01 and use the given information to complete parts​ (a) and​ (b) below.
Original​ claim: The mean pulse rate​ (in beats per​ minute) of a certain group of adult males is 71 bpm.
The hypothesis test results in a​ P-value of 0.0035.
 
a.      State a conclusion about the null hypothesis.​ (Reject Upper H 0 or fail to reject Upper H 0 ​.)  Choose the correct answer below.
 
A.     Reject H_o because the P-value is less than or equal to a.
B.      Reject H_o because the P-value is greater than a.
C.      Fail to reject H_o because the P-value is greater than a.
D.     Fail to reject H₀ because the P-value is less than or equal to a.
 
b.      Without using technical terms, state a final conclusion that addresses the original claim.
Which of the following is the correct conclusion?
 
A.     There is sufficient evidence to warrant rejection of the claim that the mean pulse rate (in beats per minute)
 of the group of adult males is 71 bpm.
B.      The mean pulse rate (in beats per minute) of the group of adult males is not 71 bpm.
C.      The mean pulse rate (in beats per minute) of the group of adult males is 71 bpm.
D.     There is not sufficient evidence to warrant rejection of the claim that the mean pulse rate (in beats per minute)
of the group of adult males is 71 bpm.

A certain drug is used to treat asthma. In a clinical trial of the​ drug, 27 of 257 treated subjects experienced headaches​
(based on data from the​ manufacturer). The accompanying calculator display shows results from a test of the claim that
less than 9​% of treated subjects experienced headaches.
Use the normal distribution as an approximation to the binomial distribution and assume a 0.05 significance level to
complete parts​ (a) through​ (e) below.
 
a.      Is the test​ two-tailed, left-tailed, or​ right-tailed? ​
Left-tailed test
 
b.      What is the test​ statistic? z = 0.84
(Round to two decimal places as​ needed.)
 
c.       What is the​ P-value?
P-value = 0.8005
 
 
TI84 Plus
STAT | TESTS | PropZTest
P⁰: 0.09
x: 27
n: 257
Calculate Then Enter
 
z = 0.843533729
p = 0.8005349949
p(hat) = 0.1050583658
n = 257
 

 
Using the pair of values for all 10 points, find the equation of the regression line.
After removing the point with coordinates left parenthesis (1, 2) use the pairs of values for the remaining 9 points
and find the equation of the regression line.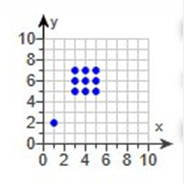
 

 
3 4 5 3 4 5 3 4 5 1
7 7 7 6 6 6 5 5 5 2
 
What is the equation of the regression line for all 10 points.
 
Ŷ = 2.766 + .766
 
STAT / Enter X,Y data / STAT / CALC / 8:LinReg (make sure xList is L1, yList L2)
A = 2.765957447
B = .7659574468

 
What is the equation of the regression line for the set of 9 points?
Ŷ = 6
(Round to three decimal places as​ needed.)
 
http://www.alcula.com/calculators/statistics/scatter-plot/
Linear regression
 
Remove 1,2 from list 1 and list 2
STAT / Enter X,Y data / STAT / CALC / 8:LinReg
6(a) – 0(b) = 6
 

 
A data set about speed dating includes​ "like" ratings of male dates made by the female dates.
The summary statistics are n = 189​, x = 7.84​, s = 1.95.
Use a 0.05 significance level to test the claim that the population mean of such ratings is less than 8.00.
Assume that a simple random sample has been selected. Identify the null and alternative​ hypotheses, test​ statistic,
P-value, and state the final conclusion that addresses the original claim.
 
HO: µ = 8.0
HO: µ < 8.0
 
Determine the test statistic. -1.13   ​
(Round to two decimal places as​ needed.)
 
TI84 Plus
STAT | TESTS | Stats| 1:Z-Test
M: 8 / o: 1.95 / X: 7.84 / N 189 / <m
or
(8 – 7.84) / 1.95 √189
 
Determine the​ P-value. 0.130   ​
(Round to three decimal places as​ needed.)
 
TI84 Plus
2nd | VARS
tcdf
lower: -9999
upper: -1.13
df: 188
enter, enter.
.129957… (round to 0.130)
 
State the final conclusion that addresses the original claim.
 
Fail to reject H0. There is not sufficient evidence to conclude that the mean of the population of ratings is less than 8.00.
 
Explanation:
If ​P-value ≤ α​ reject H₀
If ​P-value > α​ fail to reject H₀
 

 
Sixteen different video games showing drug use drug use were observed.
The duration times of drug use ​(in seconds) were recorded.
When using this sample for a t-test of the claim that the population mean is greater than 9292 ​sec,
what does df​ denote, and what is its​ value? What does df​ denote?
 
A. The sample standard deviation.
B. The test statistic.
C. The number of degrees of freedom.
D. The sample size.
 
The value of df is 15.
​(Type an integer or a decimal. Do not​ round.)
 
Sixteen (16 – 1) = 15
 

 
Fill in the blank.
In working with two variables related by a regression equation,
the _______ in a variable is the amount that it changes when the other variable changes by exactly one unit.
 
marginal change
 

 
The test statistic of z = 0.99 is obtained when testing the claim that p > 0.8
Identify the hypothesis test as being​ two-tailed, left-tailed, or​ right-tailed.
Find the​ P-value.
Using a significance level of a = 0.10​ should we reject Upper H₀ or should we fail to reject Upper H₀​?
 
This is a right-tailed test.
 
P Value = 0.161
 
Normalcdf: -9999 | .99 | 0 | 1 = 0.8389129 (round to 4 decimals)
1 - .8389 = 0.161
 
Choose the correct conclusion below.
 
A. Fail to reject Upper H₀. There is   sufficient evidence to support the claim that p > 0.8.
B. Reject Upper H₀. There is   sufficient evidence to support the claim that p > 0.8.
C. Fail to reject Upper H₀. There is not sufficient evidence to support the claim that p > 0.8.
D. Reject Upper H₀.  There is not sufficient evidence to support the claim that p > 0.8.
 

 
Claim: The mean pulse rate​ (in beats per​ minute) of adult males is equal to 68.6 bpm.
For a random sample of 128 adult​ males,
the mean pulse rate is 68.4 bpm and the standard deviation is 11.3 bpm.
Complete parts​ (a) and​ (b) below.
 
a.      Express the original claim in symbolic form.
 
µ = 68.6
(Type an integer or a decimal. Do not​ round.)
 
b.      Identify the null and alternative hypotheses.
 
H₀: µ = 68.6
H₁: P ≠ 68.6
 

 
Suppose that in a random selection of 100 colored​ candies, 21% of them are blue.
The candy company claims that the percentage of blue candies is equal to 26%.
Use a 0.01 significance level to test that claim.
 
Identify the null and alternative hypotheses for this test. Choose the correct answer below.
 
H₀​: p = 0.26
H₀​: p ≠ 0.26
 
Null hypothesis: H₀: p = 0.26
Alternative hypothesis: H₀: 0≠ 0.26
 
Identify the test statistic for this hypothesis test.
The test statistic for this hypothesis test is -1.14
​(Round to two decimal places as​ needed.)
 
TI84 Plus
STAT | TESTS
PropZTest: P: = .26 | x = 21 | n = 100 | ≠p
Z = -1.139901891
 
Identify the​ P-value for this hypothesis test.
The​ P-value for this hypothesis test is 0.254
​(Round to three decimal places as​ needed.)
 
TI84 Plus
2^nd | VARS
Normalcdf: -9999 | -1.14 | 0 | 1 = .12714132013 x 2
.12714132013 x 2 = .2542
https://www.graphpad.com/quickcalcs/pvalue1.cfm
 
Identify the conclusion for this hypothesis test.
 
A.     Fail to reject Upper H₀. There is not sufficient evidence to warrant rejection of the claim that the percentage
of blue candies is equal to 26 %
 
B.      Reject Upper H₀. There is not sufficient evidence to warrant rejection of the claim that the percentage
of blue candies is equal to 26​% .
 
C.      Reject Upper H₀. There is sufficient evidence to warrant rejection of the claim that the percentage
of blue candies is equal to 26%.
 
D.     Fail to reject Upper H₀. There is sufficient evidence to warrant rejection of the claim that the percentage
of blue candies is equal to 26%.
 

 
Different hotels in a certain area are randomly​ selected, and their ratings and prices were obtained online.
Using​ technology, with x representing the ratings and y representing​ price,
we find that the regression equation has a slope of 140 and a​ ŷ of -388
Complete parts​ (a) and​ (b) below.
 
a.      What is the equation of the regression​ line?
Select the correct choice below and fill in the answer boxes to complete your choice.
 
ŷ = -388 + (140)x
 
Explanation:
The values are given as the slope: 140 and a​ ŷ of -388
 
 
b.      What does the symbol Modifying Above y with caret represent?
 
A. The symbol ŷ represents the average price of hotels in the area.
B. The symbol ŷ with represents the expected price when the​ hotel's rating is 0.
C. The symbol ŷ represents the predicted value of price.
D. The symbol ŷ with represents the amount that price increases with a​ 1-point increase in rating.
 

 
The __________ is a value used in making a decision about the null hypothesis and is found by converting the sample statistic
to a score with the assumption that the null hypothesis is true.
 
test statistic
 

In a study of cell phone usage and brain hemispheric​ dominance,
an Internet survey was​ e-mailed to 6955 subjects randomly selected from an online group involved with ears.
There were 1284 surveys returned.
Use a 0.01 significance level to test the claim that the return rate is less than​ 20%.
Use the​ P-value method and use the normal distribution as an approximation to the binomial distribution.
 
Identify the null hypothesis and alternative hypothesis.
 
H₀: p = 0.20
H₁: p < 0.20
 
What is the test​ statistic z = -3.21
​(Round to two decimal places as​ needed.)
 
P = .20 | X = 1284 | N = 6955
STAT | TESTS | PropZTest: P: = .20 | x =1284 | n = 6955 | P | = -3.207563178
 
​P-value = 0.001
​(Round to three decimal places as​ needed.)
 
https://www.graphpad.com/quickcalcs/pvalue1.cfm
 
TI84 Plus
 
2^nd
VARS
Normalcdf:
lower: 9999 (this is positive for this problem)
upper: -3.21
0
1
Enter, enter.
 
-0.99933362
1 - .99933362615 = .001
 
Because the​ P-value is less than the significance​ level, reject the null hypothesis.
There is sufficient evidence to support the claim that the return rate is less than​ 20%.
 
If ​P-value ≤ α​ reject ^H0 - If ​P-value > α​ fail to reject ^H0
 

 
Assume a significance level of a = 0.01 and use the given information to complete parts​ (a) and​ (b) below.
Original​ claim: The mean pulse rate​ (in beats per​ minute) of a certain group of adult males is 71 bpm.
The hypothesis test results in a​ P-value of 0.0035.
 
a.      State a conclusion about the null hypothesis. (Reject H₀ or fail to reject H₀.)
Choose the correct answer below.
 
A.     Reject H₀ because the P-value is less than or equal to.
B.      Reject H₀ because the P-value is greater than
C.      Fail to reject H₀ because the P-value is greater than a.
D.     Fail to reject H₀ because the P-value is less than or equal to a.
 
b.      Without using technical terms, state a final conclusion that addresses the original claim. Which of the following is the correct conclusion?
 
A.     There is sufficient evidence to warrant rejection of the claim that the mean pulse rate
(in beats per minute) of the group of adult males is 71 bpm.
 
B.      The mean pulse rate (in beats per minute) of the group of adult males is not 71 bpm.
 
C.      The mean pulse rate (in beats per minute) of the group of adult males is 71 bpm.
 
D.     There is not sufficient evidence to warrant rejection of the claim that the mean pulse rate
            (in beats per minute) of the group of adult males is 71 bpm.
 

 
Claim: The mean pulse rate​ (in beats per​ minute) of adult males is equal to 69 bpm.
For a random sample of 159 adult​ males, the mean pulse rate is 67.9 bpm and the standard deviation is 11.1 bpm.
 
Find the value of the test statistic.
The value of the test statistic is negative -1.25
​(Round to two decimal places as​ needed.)
 
 
STAT > TESTS > Z-Test > STATS
µ: 67.9
σ: 11.1
x: 69
n: 159
≠ m (make sure this is highlighted)
Z = 1.249592093 (round to 1.25)
 
*Note this problem requires all the steps > STAT > TESTS > Z-Test > STATS
or
(67.9 – 69) / 11.1 √159
 
√ = square root.