|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Elementary Statistics Homework 1 2 3 4
5-6 6.3-7
8-10 | Tests Chapter 1-3
4 5-6 6.3-7 8-10 Final Review
Elementary Statistics
(STA2023) - Final Review
You can practice before the Final Exam. I have the solutions for a lot of these problems, however, they are repeat problems from the homeworks and tests, so I did not include all of the details again. Refer to the table summarizing
service times (seconds) of dinners at a fast food
restaurant.
How many individuals are included in
the summary? Is it possible to identify the exact values of all of the original service times?
Time (sec) Frequency 60 to 119 7 120 to 179 22 180 to 239 13 240 to 299 2 300 to 359 4 (Type a whole number.) 48 individuals are included in the summary. *Add the Frequency List Is it possible to identify the exact values of all of the original service times? A. Yes. The data values in each class are spread evenly across the full length of the class. B. Yes. The data values in each class are equal to the corresponding class midpoint. C. No. The frequency distribution tells nothing about the data values that fall below the lowest class limit or above the highest class limit. D. No. The data values in each class could take on any value between the class limits, inclusive. Listed below are selling prices (dollars) of TVs that are 60 inches or larger and rated as a "best buy" by a popular magazine. Are the resulting statistics representative of the population of all TVs that are 60 inches and larger? If you decide to buy one of these TVs, what statistic is most relevant, other than the measures of central tendency? 1950, 1100, 1400, 1100, 1800, 1200, 1100, 1150, 1200, 1000, 1100, 1450 a. Find the mean. The mean is 1295.8 (Type an integer or a decimal rounded to one decimal place as needed.) b. Find the median. The median is 1175 (Type an integer or a decimal rounded to one decimal place as needed.) Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The mode(s) is(are) 1100 (Type an integer or a decimal. Do not round. Use a comma to separate answers as needed.) B. There is no mode. d. Find the midrange. The midrange is 1475 (Type an integer or a decimal rounded to one decimal place as needed.) https://miniwebtool.com/midrange-calculator/ Add the least and greatest numbers, then divide by 2 (1000 + 1950) / 2 = 1475 https://www.calculatorsoup.com/calculators/statistics/mean-median-mode.php Are the resulting statistics representative of the population of all TVs that are 60 inches and larger? A. Since the sample is random and the sample size is greater than 10, the sample should not be considered to be representative of the population. B. The sample consists of the "best buy" TVs, so it is a random sample and is likely to be representative of the population. C. The sample consists of the "best buy" TVs, so it is not a random sample and is not likely to be representative of the population. D. Since the sample is random and the sample size is greater than 10, the sample can be considered to be representative of the population. If you decide to buy one of these TVs, what statistic is most relevant, other than the measures of central tendency? Choose the best answer below. A. The highest price is a relevant statistic for someone planning to buy one of the TVs. B. The price that occurs least frequently is a relevant statistic for someone planning to buy one of the TVs. C. The lowest price is a relevant statistic for someone planning to buy one of the TVs. D. The difference between the lowest price and the highest price is a relevant statistic for someone planning to buy one of the TVs. A frequency table of grades has five classes (A,B,C,D,F,) with frequencies of 3, 13, 15, 7 and 3 respectively. What are the relative frequencies of the five classes? Complete the table. Grade Frequency Relative frequency A 3 / 41 = 7.32 B 13 / 41 = 31.71 C 15 / 41 = 36.59 D 7 / 41 = 17.07 F 3 / 41 = 7.32 (Round to two decimal places as needed.) 41 individuals 3/41 x 100 = 7.32% Etc… A random sample of 10 subjects have weights with a standard deviation of 12.0209 kg. What is the variance of their weights? Be sure to include the appropriate units with the result. The variance of the sample data is 144.5020 kg2 (Round to four decimal places as needed.) 12.02092 (use the actual square root function not the preset) Identify the lower class limits, upper class limits, class width, class midpoints, and class boundaries for the given frequency distribution. Also identify the number of individuals included in the summary. Age (yr) Frequency 15 to 24 27 25 to 34 32 35 to 44 12 45 to 54 2 55 to 64 5 65 to 74 2 75 to 84 2 Identify the lower-class limits. 15, 25, 35, 45, 55, 65, 75 Identify the upper-class limits. 24, 34, 44, 54, 64, 74, 84 Identify the class width. 10 (Type an integer or a decimal. Do not round.) 25 – 15 = 10 Identify the class midpoints. 19.5, 29.5, 39.5, 49.5, 59.5, 69.5, 79.5 Upper Class + Lower Class / 2 Identify the Class Boundaries 14.5, 24.5, 34.5, 44.5, 54.5, 64.5, 74.5, 84.5 24 + 34 / 2 = 24.5, repeat | subtract and add class width to first and last Identify the number of individuals included in the summary. 82 (Type an integer or a decimal. Do not round.) Add Frequency List Does the frequency distribution appear to have a normal distribution using a strict interpretation of the relevant criteria?   Does the frequency distribution appear to have a normal distribution using a strict interpretation of the relevant criteria? Does the frequency distribution appear to have a normal distribution? Explain. 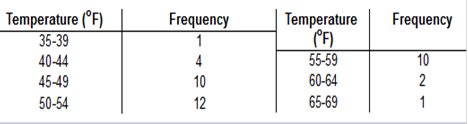 A. No, the frequencies do not decrease from the maximum frequency to a low frequency. B. Yes, all the requirements are met. C. No, the distribution does not appear to be normal. Among fatal plane crashes that occurred during the past 55 years, 622 were due to pilot error, 69 were due to other human error, 302 were due to weather, 51 were due to mechanical problems, and 77 were due to sabotage. Construct the relative frequency distribution. What is the most serious threat to aviation safety, and can anything be done about it? Complete the relative frequency distribution below. 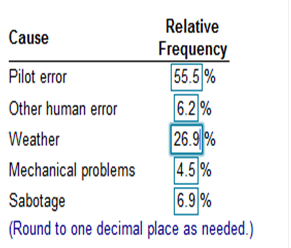 Add numbers and divide by each | multiply by 100 What is the most serious threat to aviation safety, and can anything be done about it? A. Pilot error is the most serious threat to aviation safety. Pilots could be better trained. B. Sabotage is the most serious threat to aviation safety. Airport security could be increased. C. Weather is the most serious threat to aviation safety. Weather monitoring systems could be improved. D. Mechanical problems are the most serious threat to aviation safety. New planes could be better engineered. The table below shows the frequency distribution of the rainfall on 52 consecutive Wednesdays in a certain city. Use the frequency distribution to construct a histogram. Do the data appear to have a distribution that is approximately normal 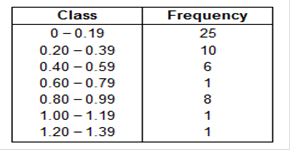 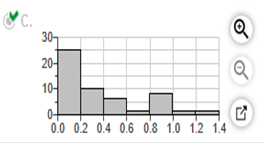 Do the data appear to have a distribution that is approximately normal? A. No, it is approximately uniform. B. Yes, it is approximately normal. C. No, it is not symmetric. D. No, it has no obvious maximum The table shows the magnitudes of the earthquakes that have occurred in the past 10 years. Does the histogram appear to be skewed? If so, identify the type of skewness.  The distribution of the data is Skewed to the right. A certain group of test subjects had pulse rates with a mean of 75.7 beats per minute and a standard deviation of 12.7 beats per minute. Use the range rule of thumb to identify the limits separating values that are significantly low or significantly high. Is a pulse rate of 111.1 beats per minute significantly low or significantly high? significantly low values are 50.3 beats per minute or lower. (Type an integer or a decimal. Do not round.) 75.7 – (2 x 12.7) = 50.3 Significantly high values are 101.1 beats per minute or higher. (Type an integer or a decimal. Do not round.) 75.7 + (2 x 12.7) = 101.1 https://www.desmos.com/scientific Is a pulse rate of 111.1 beats per minute significantly low or significantly high? A. Neither, because it is within two standard deviations of the mean. B. Significantly high, because it is greater than two standard deviations above the mean. C. Significantly low, because it is less than two standard deviations below the mean. D. It is impossible to determine with the information given The histogram to the right represents the weights (in pounds) of members of a certain high-school debate team. What is the class width? What are the approximate lower and upper class limits of the first class? 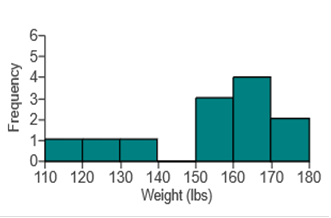 What is the class width? 10 120 – 110 = 10 What are the approximate lower and upper class limits of the first class? The approximate lower-class limit is 110. The approximate upper-class limit is 120. The graph to the right compares teaching salaries of women and men at private colleges and universities. What impression does the graph create? Does the graph depict the data fairly? If not, construct a graph that depicts the data fairly. 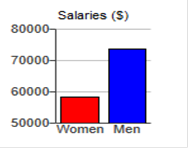 What impression does the graph create? A. The graph creates the impression that men have salaries that are more than twice the salaries of women. B. The graph creates the impression that men have salaries that are slightly higher than that of women. C. The graph creates the impression that men and women have approximately the same salaries. D. The graph creates the impression that women have salaries that are slightly higher than that of men. Does the graph depict the data fairly? A. No, because the vertical scale does not start at zero. B. No, because the data are two-dimensional measurements. C. Yes, because the bars accurately represent each average. D. Yes, because the vertical scale is appropriate for the data If the graph does not depict the data fairly, which graph below does? 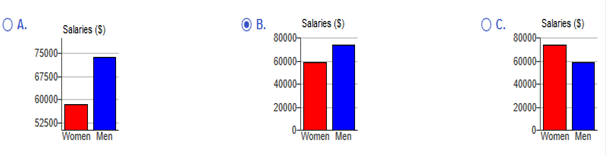 The table lists weights (pounds) and highway mileage amounts (mpg) for seven automobiles. Use the sample data to construct a scatterplot. Use the first variable for the x-axis. Based on the scatterplot, what do you conclude about a linear correlation? Weight (lb) Highway (mpg) 2725 35 2915 34 3465 28 3915 25 4050 24 2280 38 3445 30 Which scatterplot below shows the data? http://www.alcula.com/calculators/statistics/scatter-plot/  Using Excel / ENTER DATA / SELECT INSERT / SEE ALL CHARTS / SCATTER Is there a linear relationship between weight and highway mileage? A. Yes, as the weight increases the highway mileage decreases. B. No, there appears to be a relationship, but it is not linear. C. Yes, as the weight increases the highway mileage increases. D. No, there appears to be no relationship. Listed below are the weights in pounds of 11 players randomly selected from the roster of a championship sports team. Are the results likely to be representative of all players in that sport's league? 199 199 234 236 241 241 250 251 269 300 301 a. Find the mean. The mean is 226.6 Stat / enter data / stat / 1:1-var stats / list L1 / freqlist clear out / = mean https://www.hackmath.net/en/calculator/statistics b. Find the median. The median is 209 pound(s). Stat / enter data / stat / 1:1-var stats / list L1 / freqlist clear out / Med = median c. Find the mode. 1. The mode(s) is(are) 199,241 pound(s). (Do not round. Use a comma to separate answers as needed.) 2. There is no mode. The mode is the numbers that appear the most d. Find the midrange. The midrange is 250 pound(s). Add the lowest and highest numbers and divide by 2 e. Are the results likely to be representative of all players in that sport's league? A. The results are likely to be representative because a championship team is most likely representative of the entire league. B. The results are not likely to be representative because the median is not equal to the mean. C. The results are not likely to be representative because the median is not equal to the mode. D. The results are not likely to be representative because the championship team may not be representative of the entire league. Find the mean of the data summarized in the given frequency distribution. Compare the computed mean to the actual mean of 52.8 Low Temp (°F) Frequency 40-44 1 - 42 45-49 5 - 47 50-54 12 - 52 55-59 5 - 57 60-64 1 - 62 The mean of the frequency distribution is 52 degrees Find the midpoints 40 + 44 / 2, etc…. add them and divide by 5 Stat / enter data in L1 and L2 / stat / 1:1-var stats / = mean Which of the following best describes the relationship between the computed mean and the actual mean? A. The computed mean is close to the actual mean because the difference between the means is more than 5% of the actual mean. B. The computed mean is close to the actual mean because the difference between the means is less than 5% of the actual mean. C.The computed mean is not close to the actual mean because the difference between the means is less than 5% of the actual mean. D. The computed mean is not close to the actual mean because the difference between the means is more than 5% of the actual mean Compare the computed mean to the actual mean of 47.2 miles per hour. Speed (mph) Frequency 42-45 43.5 25 46-49 47.5 15 50-53 51.5 7 54-57 55.5 3 58-61 59.5 1 The mean of the frequency distribution is 46.8 miles per hour. (Round to the nearest tenth as needed.) Stat / enter data in L1 and L2 / stat / calc / 1:1-var stats / List L1 / FreqList L2 = = 46.79411765 Which of the following best describes the relationship between the computed mean and the actual mean? A. The computed mean is close to the actual mean because the difference between the means is more than 5%. B. The computed mean is not close to the actual mean because the difference between the means is more than 5%. C. The computed mean is close to the actual mean because the difference between the means is less than 5%. D. The computed mean is not close to the actual mean because the difference between the means is less than 5%. Below are the jersey numbers of 11 players randomly selected from a football team. Find the range, variance, and standard deviation for the given sample data. What do the results tell us? 8 16 20 24 26 27 33 35 38 76 90 Range = 82 (Round to one decimal place as needed.) Maximum – Minimum Sample standard deviation = 25.1 (Round to one decimal place as needed.) Stat / enter data in L1 and L2 / stat / calc / 1:1-var stats / List L1 / FreqList L2 / Sx = Sample variance = 629.4 (Round to one decimal place as needed.) Square Sx before rounding aND check below 8 16 20 24 26 27 33 35 38 76 90 https://www.hackmath.net/en/calculator/standard-deviation https://miniwebtool.com/variance-calculator/ What do the results tell us? A. Jersey numbers are nominal data that are just replacements for names, so the resulting statistics are meaningless. B. Jersey numbers on a football team vary much more than expected. C. The sample standard deviation is too large in comparison to the range. D. Jersey numbers on a football team do not vary as much as expected. Find the standard deviation, s, of sample data summarized in the frequency distribution table below by using the formula below, where x represents the class midpoint, f represents the class frequency, and n represents the total number of sample values. Also, compare the computed standard deviation to the standard deviation obtained from the original list of data values, 11.1 Interval Frequency 20-29 1 = 24.5 (20 + 29 / 2 = 24.2) 30-39 2 = 34.5 (use the pattern from above) 40-49 1 = 44.5 50-59 3 = 54.5 60-69 15 = 64.5 70-79 39 = 74.5 80-89 39 = 84.5 Standard Deviation equals 11.5 Find the midpoints 40 + 44 / 2, etc…. Stat / enter data in L1 and L2 / stat / 1:1-var stats /list L1 / freqlist L2 / Sx = Useful Online Statistics Calculator https://www.hackmath.net/en/calculator/standard-deviation Consider a difference of 20% between two values of a standard deviation to be significant. How does this computed value compare with the given standard deviation, 11.1? The computed value is significantly less than the given value. The computed value is significantly greater than the given value. The computed value is not significantly different from the given value. Consider a difference of 20% between two values of a standard deviation to be significant. 11.5 – 11.1 / 11.5 = 3.48% not significant Use z scores to compare the given values. In a recent awards ceremony, the age of the winner for best actor was 31 and the age of the winner for best actress was 47. For all best actors, the mean age is 44.1 years and the standard deviation is 8.2 years. For all best actresses, the mean age is 31.5 years and the standard deviation is 12.8 years. (All ages are determined at the time of the awards ceremony.) Relative to their genders, who had the more extreme age when winning the award, the actor or the actress? Explain. Since the z score for the actor is z = -1.60 and the z score for the actress is z = 1.21 the actor had the more extreme age. (Round to two decimal places.) 31 – 44.1 / 8.2 = -1.6 47 – 31.5 / 12.8 = 1.21 Actor Another example Since the z score for the actor is z = -1.60 and the z score for the actress is z = 1.21 the actor had the more extreme age. The blood platelet counts of a group of women have a bell-shaped distribution with a mean of 248.7 and a standard deviation of 61.8 (All units are 1000 cells/muL.) Using the empirical rule, find each approximate percentage below. a. What is the approximate percentage of women with platelet counts within 1 standard deviation of the mean, or between 186.9 and 310.5? b. What is the approximate percentage of women with platelet counts between 125.1 and 372.3? a. Approximately 68% of women in this group have platelet counts within 1 standard deviation of the mean, or between 186.9 and 310.5 (Type an integer or a decimal. Do not round.) 248.7 – (1 x 61.8) = 186.9 = 1 standard deviation away so it’s 68% = approx. 248.7 + (1 x 61.8) = 310.5 = 1 standard deviation away so it’s 68% = approx. b. Approximately 95% of women in this group have platelet counts between 125.1 and 372.3 (Type an integer or a decimal. Do not round.) 248.7 – (2 x 61.8) = 125.1 = 2 standard deviations away so it’s 95% = approx. 248.7 + (2 x 61.8) = 372.3 = 2 standard deviations away so it’s 95% = approx. About 68% of all values fall within 1 standard deviation of the mean. About 95% of all values fall within 2 standard deviations of the mean. About 99.7% of all values fall within 3 standard deviations of the mean. Instructors Tip a. The difference = highest rate - lowest rate b. answer from part a divided by s c. z = x(raw score) - mean/ s d. A z score between -2 and 2 is not significant. For a data set of the pulse rates for a sample of adult females, the lowest pulse rate is 39 beats per minute, The mean of the listed pulse rates is x overbar equals 73.0 beats per minute, and their standard deviation is equals 10.2 beats per minute. a. What is the difference between the pulse rate of 39 beats per minute and the mean pulse rate of the females? b. How many standard deviations is that [the difference found in part (a)]? c. Convert the pulse rate of 39 beats per minutes to a z score. d. If we consider pulse rates that convert to z scores between minus 2 and 2 to be neither significantly low nor significantly high, is the pulse rate of 39 beats per minute significant? The difference is 34 beats per minute. (Type an integer or a decimal. Do not round.) 73 - 39 b. The difference is 3.33 standard deviations. (Round to two decimal places as needed.) 73 – 39 / 10.2 c. The z score is z = -3.33 (Round to two decimal places as needed.) 39 – 73 / 10.2 d. The lowest pulse rate is significantly low The tallest living man at one time had a height of 230 cm. The shortest living man at that time had a height of 76.6 cm. Heights of men at that time had a mean of 173.84 cm and a standard deviation of 5.68 cm. Which of these two men had the height that was more extreme? Since the z score for the tallest man is z = 9.89 and the z score for the shortest man is z = -17.12 , the shortest man had the height that was more extreme. (Round to two decimal places.) 230 – 173.84 / 5.68 = 9.89 76.6 – 173.84 / 5.68 = -17.12 In a test of a gender-selection technique, results consisted of 298 baby girls and 18 baby boys. Based on this result, what is the probability of a girl born to a couple using this technique? Does it appear that the technique is effective in increasing the likelihood that a baby will be a girl? The probability that a girl will be born using this technique is approximately .943 (Type an integer or decimal rounded to three decimal places as needed.) 298 / (298 + 18) = .943037 Does the technique appear effective in improving the likelihood of having a girl baby? No The technique is not effective because the probability of having a girl baby is significantly lower than the expected probability of 0.5. A modified roulette wheel has 44 slots. One slot is 0, another is 00, and the others are numbered 1 through 42, respectively. You are placing a bet that the outcome is an odd number (In roulette, 0 and 00 are neither odd nor even.) a. What is your probability of winning? The probability of winning is 21/44 (Type an integer or a simplified fraction.) 42 / 2 = 21 / 44 b. What are the actual odds against winning? The actual odds against winning are 23:21 44 – 21 = 23 = 23:21 c. When you bet that the outcome is an even number, the payoff odds are 1:1. How much profit do you make if you bet $16 and win? If you win, the payoff is $16 d. How much profit should you make on the $16 bet if you could somehow convince the casino to change its payoff odds so that they are the same as the actual odds against winning? $17.52 (Round to the nearest cent as needed.) 23 x 16 / 21 = $17.52 Assume that orders are randomly selected from those included in the table. Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 325 267 250 130 Order Not Accurate 39 50 37 20 If one order is selected, find the probability of getting food that is not from Restaurant A. The probability of getting food that is not from Restaurant A is .674 (Round to three decimal places as needed.) Since we are looking for data that is NOT from, we subtract from 1 Add the data tables = 1118 Add the data in restaurant A, subtract from 1 and divide by the total data set 325 + 267 + 250 + 130 + 39 + 50 + 37 + 20 = 1118 1 – (325 + 39) / 1118 = .674 Online calculator https://www.desmos.com/scientific Use the data in the following table, which lists drive-thru order accuracy at popular fast food chains. Assume that orders are randomly selected from those included in the table. Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 333 277 244 120 Order Not Accurate 31 56 39 14 The probability of getting an order from Restaurant A or an order that is accurate is .902 (Round to three decimal places as needed.) Total = 1114 Restaurant A + Accurate (don’t add 333 twice) 333 + 31 + 277 + 244 + 120 = 1005 1005 / 1114 = .9021543986 https://www.desmos.com/scientific Are the events of selecting an order from Restaurant A and selecting an accurate order disjoint events? The events are not disjoint because it is possible to receive an accurate order from Restaurant A Recall that events A and B are disjoint (or mutually exclusive) if they cannot occur at the same time. Use the fact that there is overlap between orders from Restaurant A and orders that are accurate to determine if the events are disjoint. Use the data in the following table, which lists drive-thru order accuracy at popular fast food chains. Assume that orders are randomly selected from those included in the table. Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 316 269 243 127 Order Not Accurate 30 58 38 17 If three different orders are selected, find the probability that they are all from restaurant Upper C. The probability is 0.0168 (Round to four decimal places as needed.) https://www.desmos.com/scientific add restaurant c and divide by the total data to the 3rd power. (281 / 1098)3 = .0167614636 Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 325 267 250 130 Order Not Accurate 39 50 37 20 If one order is selected, find the probability of getting food that is not from Restaurant A. The probability of getting food that is not from Restaurant A is .674 (Round to three decimal places as needed.) https://www.desmos.com/scientific 325 + 267 + 250 + 130 + 39 + 50 + 37 + 20 = 1118 1 – (325 + 39) / 1118 = .674 Assume that orders are randomly selected from those included in the table. Drive-thru Restaurant Restaurant A Restaurant B Restaurant C Restaurant D Order Accurate 337 261 237 127 Order Not Accurate 37 50 39 14 If two orders are selected, find the probability that they are both accurate. Complete parts (a) and (b) below. a. Assume that the selections are made with replacement. Are the events independent? The probability is .762. The events are independent. (Round to three decimal places as needed.) https://www.desmos.com/scientific 962 / 1102 x 962 / 1102 = .7620561197 b. Assume that the selections are made without replacement. Are the events independent? The probability is .762 The events are not independent. (Round to three decimal places as needed.) 962 / 1102 x 961 / 1101 = .7619553912 In an experiment, college students were given either four quarters or a $1 bill and they could either keep the money or spend it on gum. The results are summarized in the table. Complete parts (a) through (c) below. Purchased Gum Kept the Money Students Given Four Quarters 32 15 Students Given a $1 Bill 17 27 a Find the probability of randomly selecting a student who spent the money, given that the student was given four quarters. The probability is 0.681 (Round to three decimal places as needed.) 32 / (32 + 15) = 32 / 47 = 0.6808510638 b. Find the probability of randomly selecting a student who kept the money, given that the student was given four quarters. The probability is 0.319 (Round to three decimal places as needed.) 15 / (32 + 15) = 15 / 47 = 0.3191489362 c. What do the preceding results suggest? A. A student given four quarters is more likely to have kept the money than a student given a $1 bill. B. A student given four quarters is more likely to have spent the money than a student given a $1 bill. C. A student given four quarters is more likely to have spent the money. D. A student given four quarters is more likely to have kept the money. The results are summarized in the table. Complete parts (a) through (c) below. Purchased Gum Kept the Money Students Given Four Quarters 26 11 Students Given a $1 Bill 12 28 a. Find the probability of randomly selecting a student who spent the money, given that the student was given a $1 bill. The probability is 0.300. (Round to three decimal places as needed.) 12 / 12 + 28 = .300 b. Find the probability of randomly selecting a student who kept the money, given that the student was given a $1 bill. The probability is 0.700 (Round to three decimal places as needed.) 28 / 12 + 28 = .700 c. What do the preceding results suggest? A. A student given a $1 bill is more likely to have spent the money. B. A student given a $1 bill is more likely to have kept the money than a student given four quarters. C. A student given a $1 bill is more likely to have kept the money. D. A student given a $1 bill is more likely to have spent the money than a student given four quarters. Find the probability of getting someone who tests positive, given that he or she had the disease. The individual actually had the disease Yes No Positive 137 5 Negative 24 134 The probability is approximately 0.851 (Round to three decimal places as needed.) 137 / (137 + 24) 137 / 161 = .850931677 Find the probability of getting someone who tests negative, given that he or she did not have the disease. 0.9640 134 / (134 + 5) = .964028777 There are 14 qualified candidates, and officers can also serve on the committee. b. How many different ways can the committee be appointed? There are 364 different ways to appoint the committee. 14 | MATH PRB nCr| 3 | ENTER (14!) / (3! (14 – 3)!) ! -> MATH | PRB https://www.desmos.com/scientific/ Click the FUNC Link, nCr(14,3) c. What is the probability of randomly selecting the committee members and getting the three youngest of the qualified candidates? P (getting the three youngest of the qualified candidates) = 1 / 364 (Type an integer or a simplified fraction.) and chief financial officer (CFO). It must also appoint a planning committee with five different members. There are 15 qualified candidates, and officers can also serve on the committee. Complete parts (a) through (c) below. How many different ways can the officers be appointed? There are 32,760 different ways to appoint the officers. 4 = president + CEO + COO + CFO 15 qualified candidates 15 | MATH PRB nPr| 4 | ENTER = 32760 or https://www.desmos.com/scientific/ Click the FUNC Link, nPr(15,4) How many difference ways to appoint to the committee? There are 3003 ways to appoint to the committee 5 = president + CEO + COO + CFO + officers 15 | MATH PRB nCr| 5 | ENTER = 3003 Or https://www.desmos.com/scientific/ Click the FUNC Link, nCr(15,5) c. What is the probability of randomly selecting the committee members and getting the five youngest of the qualified candidates? P(getting the five youngest of the qualified candidates) = 1 / 3003 (Type an integer or a simplified fraction.) the X-linked genetic disorder. Determine whether a probability distribution is given. If a probability distribution is given, find its mean and standard deviation. If a probability distribution is not given, identify the requirements that are not satisfied. x P(x) 0 0.034 1 0.145 2 0.321 3 0.321 4 0.145 5 0.034 Does the table show a probability distribution? Select all that apply. Yes, the table shows a probability distribution. P(x) needs to equal 1 https://www.mathportal.org/calculators/statistics-calculator/probability-distributions-calculator.php Stat / enter data in L1 and L2 / stat / 1:1-var stats /list L1 / freqlist L2 / σ = Find the mean of the random variable x. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. u = 2.5 child(ren) (Round to one decimal place as needed.) 0 x .034 + 1 x .145 + 2 x .321, etc.. Find the standard deviation of the random variable x. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. σ = 1.1 child(ren) (Round to one decimal place as needed.) Your answer is correct. B. The table does not show a probability distribution. x P(x) 0 0.004 1 0.019 2 0.038 3 0.113 4 0.195 5 0.239 6 0.206 7 0.117 8 0.037 9 0.015 10 0.017 Use the range rule of thumb to identify a range of values that are not significant. The maximum value in this range is 8.5 girls. (Round to one decimal place as needed.) https://www.mathportal.org/calculators/statistics-calculator/probability-distributions-calculator.php Stat / enter data in L1 and L2 / stat / 1:1-var stats /list L1 / freqlist L2 / = = Maximum = + 2() The minimum value in this range is 1.7 girls. Minimum Value = – 2(σ) Based on the result, is 1 girl in 10 births a significantly low number of girls? Explain. C. Yes, 1 girl is a significantly low number of girls, because 1 girl is below the range of values that are not significant. x P(x) 0 0.192 1 0.354 2 0.295 3 0.129 4 0.027 5 0.003 The mean is 1.5 sleepwalker(s). (Round to one decimal place as needed.) The standard deviation is sleepwalker(s). 1.0 (Round to one decimal place as needed.) https://www.mathportal.org/calculators/statistics-calculator/probability-distributions-calculator.php Stat / enter data in L1 and L2 / stat / 1:1-var stats /list L1 / freqlist L2 / = = Based on a survey, assume that 35% of consumers are comfortable having drones deliver their purchases. Suppose that we want to find the probability that when five consumers are randomly selected, exactly three of them are comfortable with delivery by drones. Identify the values of n, x, p, and q. The value of n is 5 (five) (Type an integer or a decimal. Do not round.) The value of x is 3 (three) (Type an integer or a decimal. Do not round.) The value of p is .35 (Type an integer or a decimal. Do not round.) The value of q is .65 (Type an integer or a decimal. Do not round.) 1 - .35 = .65 Assume that random guesses are made for nine multiple choice questions on an SAT test, so that there are n = 9 trials, each with probability of success (correct) given by p = 0.4 Find the indicated probability for the number of correct answers. Find the probability that the number x of correct answers is fewer than 4. P (x < 4) = .4826 (Round to four decimal places as needed.) 2nd / VARS / Binomcdf (9,.4,3): Trails = 9 / P: 0.4 / X value = (4 – 1 = 3) .482609664 Assume that random guesses are made for 4 multiple-choice questions on a test with 5 choices for each question, so that there are n = 4 trials, each with probability of success (correct) given by p = 0.20. Find the probability of no correct answers. The probability of no correct answers is .410 (Round to three decimal places as needed.) 2nd / VARS / B: Binomcdf Trails = 4 / P: .20 / X value 0 Assume that when adults with smartphones are randomly selected, 53% use them in meetings or classes. If 8 adult smartphone users are randomly selected, find the probability that exactly 3 of them use their smartphones in meetings or classes. The probability is .1912 (Round to four decimal places as needed.) binompdf : Trials 8 / P: .53 / X value: 3 .191207501 Assume that when adults with smartphones are randomly selected, 55% use them in meetings or classes. If 7 adult smartphone users are randomly selected, find the probability that exactly 5 of them use their smartphones in meetings or classes. The probability is .2140 (Round to four decimal places as needed.) binompdf : Trials 7 / P: .55 / X value: 5 .2140216805 Assume that when adults with smartphones are randomly selected, 45% use them in meetings or classes. If 13 adult smartphone users are randomly selected, find the probability that fewer than 3 of them use their smartphones in meetings or classes. The probability is .0269 (Type an integer or decimal rounded to four decimal places as needed.) binomcdf : Trials 13 / P: .45 / X value: 2 (3-1) = .0269081783 Assume that different groups of couples use a particular method of gender selection and each couple gives birth to one baby. This method is designed to increase the likelihood that each baby will be a girl, but assume that the method has no effect, so the probability of a girl is 0.5 Assume that the groups consist of 23 couples. Complete parts (a) through (c) below. a. Find the mean and the standard deviation for the numbers of girls in groups of 23 births. The value of the mean is μ = 11.5 (Type an integer or a decimal. Do not round.) 23 / .5 = 11.5 The value of the standard deviation = 2.4 (Round to one decimal place as needed.) √(23)(.5)(1-.5) = 2.397915762 Use the range rule of thumb to find the values separating results that are significantly low or significantly high. Values of 6.7 girls or fewer are significantly low. (Round to one decimal place as needed.) Values of 16.3 girls or higher are significantly high. (Round to one decimal place as needed.) 11.5 – 2(2.4) = 6.7 11.5 + 2(2.4) = 16.3 Is the result of 21 girls a result that is significantly high? What does it suggest about the effectiveness of the method? The result is significantly high, because 21 girls is greater than 16.3 girls. A result of 21 girls would suggest that the method is effective. (Round to one decimal place as needed.) In a test of the effectiveness of garlic for lowering cholesterol, 42 subjects were treated with garlic in a processed tablet form. Cholesterol levels were measured before and after the treatment. The changes (before - after) in their levels of LDL cholesterol (in mg/dL) have a mean of 4.8 and a standard deviation of 19.6. Construct a 90 % confidence interval estimate of the mean net change in LDL cholesterol after the garlic treatment. What does the confidence interval suggest about the effectiveness of garlic in reducing LDL cholesterol? What is the confidence interval estimate of the population mean mu? -0.29 mg/dL < μ < 9.89 mg/dL (Round to two decimal places as needed.) 1.0 - .09 / 2 = .05 42 – 1 = 41 invT: .05 / 41 = 1.683 (round to 3 decimals) 1.683(19.6 / √42) = 5.090 (round to 3 decimals) 4.8 – 5.090 = -.29 4.8 + 5.090 = 9.89 What does the confidence interval suggest about the effectiveness of the treatment? A. The confidence interval limits contain 0, suggesting that the garlic treatment did affect the LDL cholesterol levels. B. The confidence interval limits contain 0, suggesting that the garlic treatment did not affect the LDL cholesterol levels. C. The confidence interval limits do not contain 0, suggesting that the garlic treatment did not affect the LDL cholesterol levels. D. The confidence interval limits do not contain 0, suggesting that the garlic treatment did affect the LDL cholesterol levels. Use the calculator to find the indicated critical value. z0.04 z0.04 = 1.75 (Round to two decimal places as needed.) 1 - .04 = .96 2nd VARS / invNorm: .96 / 01 / 1 = 1.750686071 Find the indicated critical value. z0.07 = 1.48 1 - .07 = .93 2nd VARS / invNorm: .93 / 01 / 1 = 1.47579 Find the area of the shaded region. The graph depicts the standard normal distribution of bone density scores with mean 0 and standard deviation 1. 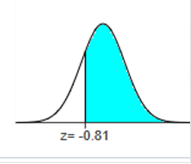 -0.81 The area under the curve to the right of the vertical line is shaded. The area of the shaded region is .7910 (Round to four decimal places as needed.) Normalcdf: Lower: -9999 / Upper: -.81 / Mu: 0 / Sd: 1 = .2089700253 1 - .2089700253 = .7910299747  70 The area of the shaded region is .0228 (Round to four decimal places as needed.) Use the NEGATIVE on ti84 70 – 100 / 15 = -2 Normalcdf: Lower: -9999 / Upper: -2 / Mean: 0 .022750062 Assume that a randomly selected subject is given a bone density test. Bone density test scores are normally distributed with a mean of 0 and a standard deviation of 1. Draw a graph and find Upper P7, the 7th percentile. This is the bone density score separating the bottom 7% from the top 93 %. Which graph represents Upper P7 Choose the correct graph below.  The bone density score corresponding to Upper P7 is -1.48 (Round to two decimal places as needed.) P7 = .07 invNormal: .07 / 0 / 1 = -1.475791028 Find the area of the shaded region. The graph to the right depicts IQ scores of adults, and those scores are normally distributed with a mean of 100 and a standard deviation of 15  98 The area of the shaded region is .5517 (Round to four decimal places as needed.) 98 – 100 / 15 = -.13 Normalcdf: Lower: -9999 / Upper: .13 (positive number because it’s on the left)) / Mean: 0 / 1 .5517168235  The area of the shaded region is .6025680579 (Round to four decimal places as needed.) Normalcdf: -9999 / .26 / 0 / 1 Find the area of the shaded region. The graph to the right depicts IQ scores of adults, and those scores are normally distributed with a mean of 100 and a standard deviation of 15. 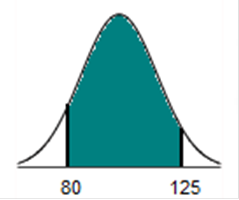 80 125 The area of the shaded region is .8607 (Round to four decimal places as needed.) 80 – 100 / 15 = -1.33 125 – 100 / 15 = 1.67 Normalcdf: -9999 / -1.33 / 0 / 1 = .0917591981 (round to 4 decimals) .0918 Normalcdf: -9999 / 1.67 / 0 / 1 = .952540341 (round to 4 decimals (.9525) .9525 - .0918 = .8607 Find the area of the shaded region. The graph depicts the standard normal distribution of bone density scores with mean 0 and standard deviation 1. 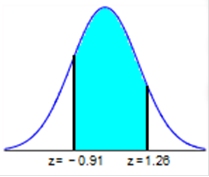 The area of the shaded region is 0.7148 (Round to four decimal places as needed.) -.91 – 0 / 1 = -.91 126 – 0 / 1 = 1.26 Normalcdf: -9999 / -.91 / 0 / 1 = .1814 (round to 4 decimals) .0918 Normalcdf: -9999 / 1.26 / 0 / 1 = .8962 (round to 4 decimals (.9525) .8962 - .1814 = .8607 Assume that adults have IQ scores that are normally distributed with a mean of mu equals 105 and a standard deviation sigma equals 20. Find the probability that a randomly selected adult has an IQ less than 129. The probability that a randomly selected adult has an IQ less than 129 is .8849 (Type an integer or decimal rounded to four decimal places as needed.) 129 – 105 / 20 = 1.2 Normalcdf: Lower: -9999 / Upper: 1.2 / Mu: 0 / SD: 1 .8849302684 Assume that adults have IQ scores that are normally distributed with a mean of 96.5 and a standard deviation of 20.7. Find the probability that a randomly selected adult has an IQ greater than 134.6 (Hint: Draw a graph.) The probability that a randomly selected adult from this group has an IQ greater than 134.6 is .0329 (Round to four decimal places as needed.) 134.6 – 96.5 / 20.7 = 1.84057971 Normalcdf: 9999 / 1.84 / 1 = -.0328840585 (remove negative) Find the critical value za/2 that corresponds to the given confidence level. 82% za/2 = 1.34 (Round to two decimal places as needed.) 100% – 82% = 1 - .82 = .18 za/2 = z.18/2 = z.09 invNorm: .09 / 0 / 1 = -1.340755035 = 1.34 (positive) 1 - .82 = .18 (enter .18) https://statscalculator.com/zcriticalvaluecalculator Critical Value of Z (Two Tailed): +1.34 Use the sample data and confidence level given below to complete parts (a) through (d). A drug is used to help prevent blood clots in certain patients. In clinical trials, among 4160 patients treated with the drug, 106 developed the adverse reaction of nausea. Construct a 99% confidence interval for the proportion of adverse reactions. Find the best point estimate of the population proportion .025 (Round to three decimal places as needed.) 106 / 4160 = .025 b) Identify the value of the margin of error E. E = .006 (Round to three decimal places as needed.) Margin of Error Ti84 plus: stat / test / A:1 – PropZint / 106 / 4160 / .99 = (.01919,.03177) = .03177 - .01919 / 2 = .00629 DON’T FORGET TO DIVIDE BY 2 Construct the confidence interval. .019 < p < .031 (Round to three decimal places as needed.) .025 - .006 = .019 .025 + .006 = .031 Write a statement that correctly interprets the confidence interval. Choose the correct answer below. A. One has 99% confidence that the interval from the lower bound to the upper bound actually does contain the true value of the population proportion. B. One has 99% confidence that the sample proportion is equal to the population proportion. C. There is a 99% chance that the true value of the population proportion will fall between the lower bound and the upper bound. D. 99% of sample proportions will fall between the lower bound and the upper bound. In a survey of 3042 adults aged 57 through 85 years, it was found that 85.1% of them used at least one prescription medication. Complete parts (a) through (c) below. How many of the 3042 subjects used at least one prescription medication? 2589 (Round to the nearest integer as needed.) 3042 x .851 = 2589 Construct a 90% confidence interval estimate of the percentage of adults aged 57 through 85 years who use at least one prescription medication. 84.0% < p < 86.2% (Round to one decimal place as needed.) Za/2 = 100% - 90% / 2 = 1 - .90 / 2 = .05 invNorm: .5 / 0 / 1 = 1.64 (rounded to 2) 1.64√.851(1 - .851) / 3042 = = .0105882005 (.0106) .851 - .0106 = .8404 X 100 = 84.0% .851 + .0106 = .8616 X 100 = 86.2% What do the results tell us about the proportion of college students who use at least one prescription medication? A. The results tell us that, with 90% confidence, the probability that a college student uses at least one prescription medication is in the interval found in part (b). B. The results tell us nothing about the proportion of college students who use at least one prescription medication. C. The results tell us that there is a 90% probability that the true proportion of college students who use at least one prescription medication is in the interval found in part (b). D. The results tell us that, with 90% confidence, the true proportion of college students who use at least one prescription medication is in the interval found in part (b). You are the operations manager for an airline and you are considering a higher fare level for passengers in aisle seats. How many randomly selected air passengers must you survey? Assume that you want to be 99% confident that the sample percentage is within 5.5 percentage points of the true population percentage. Complete parts (a) and (b) below. a. Assume that nothing is known about the percentage of passengers who prefer aisle seats. N = 548 (Round up to the nearest integer.) 100% - 99% / 2 = 1 - .99 / 2 = .005 invNorm: .005 / 0 / 1 = 2.576 (rounded to 3) Use .25 in this equation .055 for 5.5 percentages 2.5762 x .25 / .0552 = 548.411 Assume that a prior survey suggests that about 38% of air passengers prefer an aisle seat. N = 517 (Round up to the nearest integer.) 2.5762 x .38 (1 - .38) / .0552 = 516.8227 (517) The brand manager for a brand of toothpaste must plan a campaign designed to increase brand recognition. He wants to first determine the percentage of adults who have heard of the brand. How many adults must he survey in order to be 90% confident that his estimate is within five percentage points of the true population percentage? Complete parts (a) through (c) below. Assume that nothing is known about the percentage of adults who have heard of the brand. N = 271 (Round up to the nearest integer.) 1 - .9 / 2 = .05 E = .05: within five percentage points invNorm: .05 / 0 / 1 = 1.6449 (round to 4 decimals) .50 is the estimated proportion (when nothing is known, .5 is assumed) 1.64492 x .5(1 - .5) / .052 = 270.569601 Assume that a recent survey suggests that about 85% of adults have heard of the brand. n = 138 (Round up to the nearest integer.) 1.64492 x .85(1 - .85) / .052 = 137.9904 Given that the required sample size is relatively small, could he simply survey the adults at the nearest college? C. No, a sample of students at the nearest college is a convenience sample, not a simple random sample, so it is very possible that the results would not be representative of the population of adults. Watch this one because the book rounded when it shouldn’t have. Here are summary statistics for randomly selected weights of newborn girls: n=226, x=26.2 hg, s=7.2 hg. Construct a confidence interval estimate of the mean. Use a 98% confidence level. Are these results very different from the confidence interval 24.8 hg < μ <28.4 hg with only 18 sample values, x=26.6 hg, and s=2.9 hg? What is the confidence interval for the population mean mu? 25.1 hg < u < 27.3 hg (Round to one decimal place as needed.) 226 – 1 = 225 1 - .98 / 2 = .01 invT: .01 / 225 = 2.343 26.2 – (2.343 x 7.2 / √226) = 25.0778509 26.2 + (2.343 x 7.2 / √226) = 25.0778509 Are the results between the two confidence intervals very different? A. Yes, because one confidence interval does not contain the mean of the other confidence interval. B. No, because each confidence interval contains the mean of the other confidence interval. C. No, because the confidence interval limits are similar. D. Yes, because the confidence interval limits are not similar Listed below are the amounts of net worth (in millions of dollars) of the ten wealthiest celebrities in a country. Construct a 90% confidence interval. What does the result tell us about the population of all celebrities? Do the data appear to be from a normally distributed population as required? 242 210 176 160 156 154 150 150 150 150 What is the confidence interval estimate of the population mean mu? $151.5 million < u < $188.1 million (Round to one decimal place as needed.) STAT | ENTER DATA | STAT | TESTS | 8: Tinterval | data | L1 | Freq 1 | C-Level .9 | Mean = 1712 / 10 = 171.2 N = 10 – 1 = 9 1 - .90 / 2 = .05 invT: .05 / 1.833 (round to 3 decimals) or ti-84 plus: stat/edit/enter numbers stat/calc/1-var/List: L1/FreqList: blank/ calculate sample standard deviation (smaller one) Sx = 31.57 1.833 x 31.57 / √10 = 169.8 – 18.3 = 151.5 169.8 + 18.3 = 188.1 What does the result tell us about the population of all celebrities? Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. A. Because the ten wealthiest celebrities are not a representative sample, this doesn't provide any information about the population of all celebrities. Do the data appear to be from a normally distributed population as required? C. No, because the points lie reasonable close to a straight line, but there is a systematic pattern that is not a straight line pattern. The pulse rates of 176 randomly selected adult males vary from a low of 43 bpm to a high of 115 bpm. Find the minimum sample size required to Assume that we want 90% confidence that the sample mean is within 2 bpm of the population mean. Complete parts (a) through (c) below. Find the sample size using the range rule of thumb to estimate . N = 219 (Round up to the nearest whole number as needed.) 1 - .9 / 2 = .05 invNorm: .05 / 0 / 1 = 1.645 range rule of thumb = range / 4 (115 – 43) / 4 = 18 (1.645 x 18 / 2)2 = 219.188025 Assume that = 12.3 bpm, based on the value s = 12.3 bpm from the sample of 176 male pulse rates. n = 102 (Round up to the nearest whole number as needed.) (1.645 x 12.3 / 2)2 = 102.3486306 The result from part a) is larger than the result from part b). The result from part (b) is likely to be better because it uses a better estimate of σ). Salaries of 34 college graduates who took a statistics course in college have a mean, x of $60500 Assuming a standard deviation of $15003 construct a 90% confidence interval for estimating the population. $56267 < mu < $64733 (Round to the nearest integer as needed.) 1 - .9 / 2 = .05 = 1.645 (round to 3 decimals) 1.645 x 15003 / √34 = 4232.574 (round to 3 decimals) 60500 - 4232.574 = 56267.426 60500 + 4232.574 = 64732.574 Claim: The mean pulse rate (in beats per minute) of adult males is equal to 68.6 bpm. For a random sample of 128 adult males, the mean pulse rate is 68.4 bpm and the standard deviation is 11.3 bpm. Complete parts (a) and (b) below. Express the original claim in symbolic form. u = 68.6 (Type an integer or a decimal. Do not round.) Identify the null and alternative hypotheses. H0: u = 68.6 H1: P ≠ 68.6 The claim involves a population proportion This means that the appropriate parameter for the claim is μ The test statistic of z = 0.99 is obtained when testing the claim that p > 0.8 Identify the hypothesis test as being two-tailed, left-tailed, or right-tailed. Find the P-value. Using a significance level of a = 0.10 should we reject Upper H0 or should we fail to reject Upper H0 ? This is a right-tailed test P Value = .161 Normalcdf: -9999 / .99 / 0 / 1 = .8389129 (round to 4 decimals) 1 - .8389 = .161 Choose the correct conclusion below. A. Fail to reject Upper H0. There is sufficient evidence to support the claim that p > 0.8 . B. Reject Upper H0. There is sufficient evidence to support the claim that p > 0.8 . C. Fail to reject Upper H0. There is not sufficient evidence to support the claim that p > 0.8 D. Reject Upper H0. There is not sufficient evidence to support the claim that p > 0.8. ANOTHER EXAMPLE The test statistic of z = 0.93 is obtained when testing the claim that p > 0.3 P Value = .176 C. Fail to reject Upper H0. There is not sufficient evidence to support the claim that p > 0.3 The symbol > points to the right and the test is right-tailed. The symbol < points to the left and the test is left-tailed. The symbol ≠ is used for a two-tailed test. If P-value ≤ “α” reject H0 If P-value > “α” fail to reject H0 The test statistic of z = 2.31 is obtained when testing the claim that p > 0.9 Identify the hypothesis test as being two-tailed, left-tailed, or right-tailed Find the P-value Using a significance level of a = .05, should we reject Upper H 0 or should we fail to reject Upper H 0 ? This is a right-tailed test P-value = 0.010 (Round to three decimal places as needed.) Normalcdf: -9999 / 2.31 / 0 / 1 = .9895559 (round to 4 decimals) .990 1 - .990 = .01 Choose the correct conclusion below. A. Reject H 0. There is not sufficient evidence to support the claim that p > 0.9 B. Reject H0. There is sufficient evidence to support the claim that p > 0.9 C. Fail to reject H0 There is not sufficient evidence to support the claim that p > 0.9 D. Fail to reject H0 . There is sufficient evidence to support the claim that p > 0.9. If P-value ≤ α reject H0 If P-value > α fail to reject H0 The symbol > points to the right and the test is right-tailed The symbol < points to the left and the test is left-tailed. The symbol ≠ is used for a two-tailed test. Assume a significance level of a = 0.01 and use the given information to complete parts (a) and (b) below. Original claim: The mean pulse rate (in beats per minute) of a certain group of adult males is 73 bpm. The hypothesis test results in a P-value of 0.0709. a. State a conclusion about the null hypothesis. (Reject Upper H 0 or fail to reject Upper H 0 .) Choose the correct answer below. D. Fail to reject H0 because the P-value is greater than a Without using technical terms, state a final conclusion that addresses the original claim. Which of the following is the correct conclusion? C. There is not sufficient evidence to warrant rejection of the claim that the mean pulse rate (in beats per minute) of the group of adult males is 73 bpm. *** Another example **** Assume a significance level of a = 0.05 and use the given information to complete parts (a) and (b) below. Original claim: The mean pulse rate (in beats per minute) of a certain group of adult males is 71 bpm. The hypothesis test results in a P-value of 0.0089. a. State a conclusion about the null hypothesis. (Reject Upper H 0 or fail to reject Upper H 0 .) Choose the correct answer below. C. Reject H0 because the P-value is less than or equal to a Without using technical terms, state a final conclusion that addresses the original claim. Which of the following is the correct conclusion? A. There is sufficient evidence to warrant rejection of the claim that the mean pulse rate (in beats per minute) of the group of adult males is 71 bpm. Consider a drug that is used to help prevent blood clots in certain patients. In clinical trials, among 6187 patients treated with this drug, 161 developed the adverse reaction of nausea. Use a 0.05 significance level to test the claim that 3% of users develop nausea. Does nausea appear to be a problematic adverse reaction? Identify the null and alternative hypotheses for this test. Choose the correct answer below. H0: p = .03 H0: p ≠ .03 Identify the test statistic for this hypothesis test. The test statistic for this hypothesis test is -1.83 (Round to two decimal places as needed.) STAT / TEST / Stats 5:1-PropZTest: P: = .03 / x = 161 / n = 6187 / ≠p = -1.83 The P-value for this hypothesis test is 0.067 (Round to three decimal places as needed.) Normalcdf: -9999 / -1.83 / 0 / 1 = .0336249107 x 2 .0336249107 x 2 = .0672498214 Identify the conclusion for this hypothesis test. A. Fail to reject Upper H 0 . There is sufficient evidence to warrant rejection of the claim that 3 % of users develop nausea. B. Reject Upper H0. There is sufficient evidence to warrant rejection of the claim that 3 % of users develop nausea. C. Fail to reject H0. There is not sufficient evidence to warrant rejection of the claim that 3 % of users develop nausea. D. Reject Upper H 0 . There is not sufficient evidence to warrant rejection of the claim that 3 % of users develop nausea. Does nausea appear to be a problematic adverse reaction? Since the rate of nausea appears to be relatively low, it is not a problematic adverse reaction. If P-value ≤ α reject H0 If P-value > α fail to reject H0 Assume that adults were randomly selected for a poll. They were asked if they "favor or oppose using federal tax dollars to fund medical research using stem cells obtained from human embryos." Of those polled, 488 were in favor, 403 were opposed, and 118 were unsure. A politician claims that people don't really understand the stem cell issue and their responses to such questions are random responses equivalent to a coin toss. Exclude the 118 subjects who said that they were unsure, and use a 0.05 significance level to test the claim that the proportion of subjects who respond in favor is equal to 0.5 . What does the result suggest about the politician's claim? Identify the null and alternative hypotheses for this test. Choose the correct answer below. Ho: p = .5 Ho: p ≠ .5 Identify the test statistic for this hypothesis test. The test statistic for this hypothesis test is 2.85 (Round to two decimal places as needed.) Identify the P-value for this hypothesis test. The P-value for this hypothesis test is .004 (Round to three decimal places as needed.) P = .5 / x = 488 / N = 891 STAT / TEST / 5:1-PropZTest: P: = .5 / x = 488 / n = 891 / ≠p = 2.84777898 tcdf: 9999 / 2.85 / df = 890 = .9977635623 1 - .9977635623 x 2 = (.00223 x 2) = .00446 Identify the conclusion for this hypothesis test. A. Fail to reject Upper H0. There is not sufficient evidence to warrant rejection of the claim that the responses are equivalent to a coin toss. B. Fail to reject Upper H0. There is sufficient evidence to warrant rejection of the claim that the responses are equivalent to a coin toss. C. Reject H0. There is sufficient evidence to warrant rejection of the claim that the responses are equivalent to a coin toss. D. Reject H0. There is not sufficient evidence to warrant rejection of the claim that the responses are equivalent to a coin toss. What does the result suggest about the politician's claim? A. The result suggests that the politician is correct in claiming that the responses are random guesses equivalent to a coin toss. B. The result suggests that the politician is wrong in claiming that the responses are random guesses equivalent to a coin toss. C. The result suggests that the politician is doing his best to accurately portray the feelings of the people. D. The results are inconclusive about whether the politician is correct or not. If P-value ≤ α reject H0 - If P-value > α fail to reject H0 Refer to the accompanying scatterplot. a. Examine the pattern of all 10 points and subjectively determine whether there appears to be a strong correlation between x and y. b. Find the value of the correlation coefficient r and determine whether there is a linear correlation. c. Remove the point with coordinates (2,9) and find the correlation coefficient r and determine whether there is a linear correlation. d. What do you conclude about the possible effect from a single pair of values? 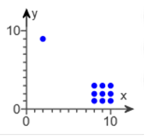 X| 8 9 10 8 9 10 8 9 10 2 | Y| 3 3 3 2 2 2 1 1 1 9 | Do the data points appear to have a strong linear correlation? Yes What is the value of the correlation coefficient for all 10 data points? r = -.880 (Simplify your answer. Round to three decimal places as needed.) http://www.alcula.com/calculators/statistics/scatter-plot/ or Turn on Diagnostics: 2nd catalog / Turn on Diagnostics On STAT / Enter X,Y data / STAT / CALC / 4:LinReg / Xlist L1 / yList L2 / FreqList: clear out / calculate r = -.880239521 Is there a linear correlation between x and y? Use α = 0.01 B. Yes, because the correlation coefficient is in the critical region. -.88 is between -.01 and 01 What is the correlation coefficient when the point (2,9) is excluded? R = 0.000 (Round to three decimal places as needed.) Turn on Diagnostics: 2nd catalog / Turn on DiagnosticsOn STAT / Enter X,Y data / STAT / CALC / 4:LinReg (make sure XList is L1, YList L2) Remove 2 and 9 | R = 0.000 Is there a linear correlation between x and y? Use alphaα = 0.01 C. No, because the correlation coefficient is not in the critical region. What do you conclude about the possible effect from a single pair of values? A single pair of values does not change the conclusion. The effect from a single pair of values can change the conclusion. Refer to the accompanying scatterplot. The four points in the lower left corner are measurements from women, and the four points in the upper right corner are from men. Complete parts (a) through (e) below. 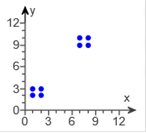 Examine the pattern of the four points in the lower left corner (from women) only, and subjectively determine whether there appears to be a correlation between x and y for women. Choose the correct answer below. A. There does not appear to be a linear correlation because the points do not form a line. Examine the pattern of the four points in the upper right corner (from men) only, and subjectively determine whether there appears to be a correlation between x and y for men. Choose the correct answer below. A. There does not appear to be a linear correlation because the points do not form a line. Find the linear correlation coefficient using only the four points in the lower left corner (for women). Will the four points in the upper right corner (for men) have the same linear correlation coefficient? http://www.alcula.com/calculators/statistics/scatter-plot The correlation coefficient for the points in the lower left corner is r = 0 (Type an integer or a fraction.) X: 7, 8, 7, 8 Y: 10, 10, 9, 9 Turn on Diagnostics: 2nd catalog / Turn on Diagnostics On STAT / Enter X,Y data / STAT / CALC / 4:LinReg (make sure xList is L1, yList L2) Do the four points in the upper right corner have the same correlation coefficient? C. Yes, because the four points in the upper right corner form the same pattern as the four points in the lower left corner. Find the value of the linear correlation coefficient using all eight points. What does that value suggest about the relationship between x and y? Use a = 0.05 The correlation coefficient for all eight points is r = .976 (Round to three decimal places as needed.) X: 7, 8, 7, 8, 1, 2, 1, 2 Y: 10, 10, 9, 9, 3, 3, 2, 2 STAT / Enter X,Y data / STAT / CALC / 4:LinReg / Xlist L1 / yList L2 / FreqList: clear out / calculate Using a = 0.05, what does r suggest about the relationship between x and y? B. There is sufficient evidence to support the claim of a linear correlation, because the correlation coefficient is greater than the critical value. Based on the preceding results, what can be concluded? Should the data from women and the data from men be considered together, or do they appear to represent two different and distinct populations that should be analyzed separately? D. There are two different populations that should be considered separately Using the pairs of values for all 10 points, find the equation of the regression line. After removing the point with coordinates left parenthesis (8,3) right parenthesis , use the pairs of values for the remaining 9 points and find the equation of the regression line. Compare the results from parts (a) and (b).  X| 1 2 3 1 2 3 1 2 3 8 Y| 5 5 5 6 6 6 7 7 7 3 What is the equation of the regression line for all 10 points Ŷ = 6.797 + -.422 STAT / Enter X,Y data / STAT / CALC / 8:LinReg (make sure xList is L1, yList L2) A = 6.796875 B = -4.21875 What is the equation of the regression line for the set of 9 points? Ŷ = 6 (Round to three decimal places as needed.) Remove 8,3 STAT / Enter X,Y data / STAT / CALC / 8:LinReg 6(a) – 0(b) = 6 Choose the correct description of the results below. A. The regression line is very similar in both cases. B. There is no regression line for the second case because the data are in a pattern. C. The regression line changes, but the change is small. D. The removal of the point has a significant impact on the regression line. Different hotels in a certain area are randomly selected, and their ratings and prices were obtained online. Using technology, with x representing the ratings and y representing price, we find that the regression equation has a slope of 140 and a y^ of -388 Complete parts (a) and (b) below. What is the equation of the regression line? Select the correct choice below and fill in the answer boxes to complete your choice. ŷ = -388 + (140) x What does the symbol Modifying Above y with caret represent? A. The symbol ŷ represents the average price of hotels in the area. B. The symbol ŷ with represents the expected price when the hotel's rating is 0. C. The symbol ŷ represents the predicted value of price. D. The symbol ŷ with represents the amount that price increases with a 1-point increase in rating. In a study of cell phone usage and brain hemispheric dominance, an Internet survey was e-mailed to 6955 subjects randomly selected from an online group involved with ears. There were 1284 surveys returned. Use a 0.01 significance level to test the claim that the return rate is less than 20%. Use the P-value method and use the normal distribution as an approximation to the binomial distribution. Identify the null hypothesis and alternative hypothesis. H 0: p = 0.20 H 1: p < 0.20 What is the test statistic z = -3.21 (Round to two decimal places as needed.) P = .20 | X = 1284 | N = 6955 STAT | TESTS | 5:PropZTest: P: = .20 / x =1284 / n = 6955 / P< / = -3.207563178 P-value = 0.001 (Round to three decimal places as needed.) https://www.graphpad.com/quickcalcs/pvalue1.cfm Normalcdf: +9999 (LEFT SIDE) / -3.21 / 0 / 1 = -.99933362 1 - .99933362615 = .001 Because the P-value is less than the significance level, reject the null hypothesis. There is sufficient evidence to support the claim that the return rate is less than 20%. If P-value ≤ α reject H0 - If P-value > α fail to reject H0 Suppose that in a random selection of 100 colored candies, 21% of them are blue. The candy company claims that the percentage of blue candies is equal to 26%. Use a 0.01 significance level to test that claim. Identify the null and alternative hypotheses for this test. Choose the correct answer below. H0: p = 0.26 H0: p ≠0.26 Identify the test statistic for this hypothesis test. The test statistic for this hypothesis test is -1.14 (Round to two decimal places as needed.) .21 x 100 = 21 5:1PropZTest: P: = .26 / x = 21 / n = 100 / ≠p = -1.139901891 Identify the P-value for this hypothesis test. The P-value for this hypothesis test is .254 (Round to three decimal places as needed.) Normalcdf: -9999 / -1.14 / 0 / 1 = .12714132013 x 2 .12714132013 x 2 = .2542 https://www.graphpad.com/quickcalcs/pvalue1.cfm Identify the conclusion for this hypothesis test. A. Fail to reject Upper H0. There is not sufficient evidence to warrant rejection of the claim that the percentage of blue candies is equal to 26 % B. Reject Upper H0. There is not sufficient evidence to warrant rejection of the claim that the percentage of blue candies is equal to 26% C. Reject Upper H0. There is sufficient evidence to warrant rejection of the claim that the percentage of blue candies is equal to 26% D. Fail to reject Upper H0. There is sufficient evidence to warrant rejection of the claim that the percentage of blue candies is equal to 26 % If P-value ≤ α reject H0 - If P-value > α fail to reject H0 Claim: The mean pulse rate (in beats per minute) of adult males is equal to 69 bpm. For a random sample of 159 adult males, the mean pulse rate is 67.9 bpm and the standard deviation is 11.1 bpm. Find the value of the test statistic. The value of the test statistic is negative -1.25 (Round to two decimal places as needed.) STATS | TESTS | Stats| 1:Z-Test M: 67.9 / o: 11.1 / X: 69 / N 159 / ≠m or (67.9 – 69) / 11.1 √159 Sixteen different video games showing drug use drug use were observed. The duration times of drug use (in seconds) were recorded. When using this sample for a t-test of the claim that the population mean is greater than 9292 sec, what does df denote, and what is its value? What does df denote? A. The sample standard deviation B. The test statistic C. The number of degrees of freedom D. The sample size The value of df is 15 (Type an integer or a decimal. Do not round.) Sixteen (16 – 1) = 15 A data set about speed dating includes "like" ratings of male dates made by the female dates. The summary statistics are n = 189, x = 7.84, s = 1.95. Use a 0.05 significance level to test the claim that the population mean of such ratings is less than 8.00. Assume that a simple random sample has been selected. Identify the null and alternative hypotheses, test statistic, P-value, and state the final conclusion that addresses the original claim. HO: u = 8.0 HO: u < 8.0 Determine the test statistic. -1.13 (Round to two decimal places as needed.) STATS | TESTS | Stats| 1:Z-Test M: 8 / o: 1.95 / X: 7.84 / N 189 / <m or (8 – 7.84) / 1.95 √189 Determine the P-value. 0.130 (Round to three decimal places as needed.) Tcdf: -9999 / -1.13 / 188 State the final conclusion that addresses the original claim. Fail to reject H0. There is not sufficient evidence to conclude that the mean of the population of ratings is less than 8.00 If P-value ≤ α reject H0 If P-value > α fail to reject H0 Using the pair of values for all 10 points, find the equation of the regression line. After removing the point with coordinates left parenthesis (1,2) use the pairs of values for the remaining 9 points and find the equation of the regression line.  3 4 5 3 4 5 3 4 5 1 7 7 7 6 6 6 5 5 5 2 What is the equation of the regression line for all 10 points Ŷ = 2.766 + .766 STAT / Enter X,Y data / STAT / CALC / 8:LinReg (make sure xList is L1, yList L2) A = 2.765957447 B = .7659574468 What is the equation of the regression line for the set of 9 points? Ŷ = 6 (Round to three decimal places as needed.) http://www.alcula.com/calculators/statistics/scatter-plot/ Linear regression Remove 1,2 from list 1 and list 2 STAT / Enter X,Y data / STAT / CALC / 8:LinReg 6(a) – 0(b) = 6 Choose the correct description of the results below. A. The regression line is very similar in both cases. B. There is no regression line for the second case because the data are in a pattern. C. The regression line changes, but the change is small. D. The removal of the point has a significant impact on the regression line. A certain drug is used to treat asthma. In a clinical trial of the drug, 27 of 257 treated subjects experienced headaches (based on data from the manufacturer). The accompanying calculator display shows results from a test of the claim that less than 9% of treated subjects experienced headaches. Use the normal distribution as an approximation to the binomial distribution and assume a 0.05 significance level to complete parts (a) through (e) below. 5:1-PropZTest prop < 0.09 z = 0.843533729 p = 0.8005349949 p(hat) = 0.1050583658 n = 257 a. Is the test two-tailed, left-tailed, or right-tailed? Left-tailed test What is the test statistic? z = 0.84 (Round to two decimal places as needed.) What is the P-value? P-value = 0.8005 p = p-value (Round to four decimal places as needed.) What is the null hypothesis, and what do you conclude about it? Identify the null hypothesis. D. H0: p = 0.09 Decide whether to reject the null hypothesis. Choose the correct answer below. D. Fail to reject the null hypothesis because the P-value is > the significance level, a If P-value ≤ α reject H0 - If P-value > α fail to reject H0 What is the final conclusion? B. There is not sufficient evidence to support the claim that less than 9% of treated subjects experienced headaches. *** Fail To Reject would be **** There is sufficient evidence to support the claim that less than 9% of treated subjects experienced headaches. If P-value ≤ α reject H0 If P-value > α fail to reject H0 The table provided below shows paired data for the heights of a certain country's presidents and their main opponents in the election campaign. Construct a scatterplot. Does there appear to be a correlation? President's_height_(cm) Opponent's_height_(cm) 189 195 178 194 194 193 196 168 169 176 174 168 173 175 193 176 191 196 176 177 194 196 193 191 173 172 172 174 179 195 172 193 Construct a scatterplot. Choose the correct graph below. 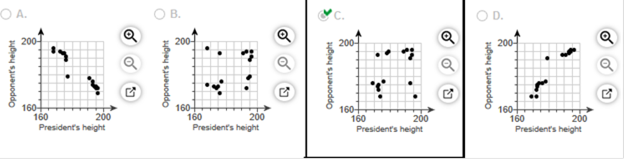 Does there appear to be a correlation between the president's height and his opponent's height? A. Yes, there appears to be a correlation. The candidate with the highest height usually wins. B. Yes, there appears to be a correlation. As the president's height increases, his opponent's height increases. C. Yes, there appears to be a correlation. As the president's height increases, his opponent's height decreases. D. No, there does not appear to be a correlation because there is no general pattern to the data Most adults would not......mean less than 50 % do not erase all of their personal information. Claim: Most adults would not erase all of their personal information online if they could. A software firm survey of 466 randomly selected adults showed that 44% of them would erase all of their personal information online if they could. Complete parts (a) and (b) below. Express the original claim in symbolic form. Let the parameter represent the adults that would erase their personal information. P < 0.50 Type an integer or a decimal. Do not round.) H0: P = 0.50 H1: P < 0.50 The claim involves a population proportion In a study of 783 randomly selected medical malpractice lawsuits, it was found that 496 of them were dropped or dismissed. Use a 0.01 significance level to test the claim that most medical malpractice lawsuits are dropped or dismissed. Which of the following is the hypothesis test to be conducted? H0: p = 0.5 H1: p > 0.5 What is the test statistic? z = 7.47 (Round to two decimal places as needed.) X = 496 | p = .5 | n = 783 5:1PropZTest: P: = .5 / x =496 / n = 783 / >p= 7.469050659 P-value = 0.000 (Round to three decimal places as needed.) https://www.graphpad.com/quickcalcs/pvalue1.cfm Normalcdf: -9999 / 7.47 / 0 / 1 = 1 x 2 = 0.000 What is the conclusion about the null hypothesis? A. Fail to reject the null hypothesis because the P-value is less than or equal to the significance level, a B. Reject the null hypothesis because the P-value is greater than the significance level, a C. Fail to reject the null hypothesis because the P-value is greater than the significance level, a D. Reject the null hypothesis because the P-value is less than or equal to the significance level, a If P-value ≤ α reject H0 - If P-value > α fail to reject H0 What is the final conclusion? A. There is not sufficient evidence to support the claim that most medical malpractice lawsuits are dropped or dismissed. B. There is not sufficient evidence to warrant rejection of the claim that most medical malpractice lawsuits are dropped or dismissed. C. There is sufficient evidence to warrant rejection of the claim that most medical malpractice lawsuits are dropped or dismissed. D. There is sufficient evidence to support the claim that most medical malpractice lawsuits are dropped or dismissed. A data set includes data from 500 random tornadoes. The display from technology available below results from using the tornado lengths (miles) to test the claim that the mean tornado length is greater than 2.6 miles. Use a 0.05 significance level. Identify the null and alternative hypotheses, test statistic, P-value, and state the final conclusion that addresses the original claim. 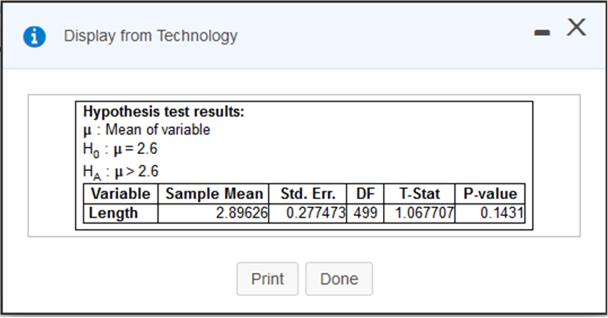 H0: μ = 2.6 Miles H0: μ > 2.6 Miles Identify the test statistic. 1.07 (Round to two decimal places as needed.) Identify the P-value 0.143 (Round to three decimal places as needed.) State the final conclusion that addresses the original claim. Fail to reject H0 There is not sufficient evidence to support the claim that the mean tornado length is greater than 2.6 miles If P-value ≤ α reject H0 - If P-value > α fail to reject H0 Claim: The mean pulse rate (in beats per minute) of adult males is equal to 69 bpm. For a random sample of 159 adult males, the mean pulse rate is 67.9 bpm and the standard deviation is 11.1 bpm. Find the value of the test statistic. The value of the test statistic is negative -1.25 (Round to two decimal places as needed.) STATS | TESTS | Stats| 1:Z-Test M: 67.9 / o: 11.1 / X: 69 / N 159 / ≠m or (67.9 – 69) / 11.1 √159 In a genetics experiment on peas, one sample of offspring contained 450 green peas and 48 yellow peas. Based on those results, estimate the probability of getting an offspring pea that is green. Is the result reasonably close to the value of 3/4 that was expected? The probability of getting a green pea is approximately nothing .904. (Type an integer or decimal rounded to three decimal places as needed.) 450 / 450 + 48 = .904 Is this probability reasonably close to three fourths ? Choose the correct answer below. A. No , it is not reasonably close. B. Yes ,it is reasonably close A genetic experiment with peas resulted in one sample of offspring that consisted of 429 green peas and 160 yellow peas. a. Construct a 90% confidence interval to estimate of the percentage of yellow peas. b. It was expected that 25% of the offspring peas would be yellow. Given that the percentage of offspring yellow peas is not 25%, do the results contradict expectations? A. Construct a 90% confidence interval. Express the percentages in decimal form. .2416 < p < .3016 (Round to three decimal places as needed.) 160 + 429 = 589 160 ÷ 589 = .2716 (rounded to 4) 1 - .90 ÷ 2 = .05 invNorm: .05 / 0 / 1 = 1.644 (rounded to 3) q = 1 - .2716 = .7284 1.64√.2716 (.7284 ÷ 589) = .030 (rounded to 4) Lower: .2716 - .0300 = .2416 Upper: .2716 + .0300 = .3016 Given that the percentage of offspring yellow peas is not 25%, do the results contradict expectations? No, the confidence interval includes 0.25, so the true percentage could easily equal 25% Yes, the confidence interval does not include 0.25, so the true percentage could not equal 25% A research center poll showed that 84% of people believe that it is morally wrong to not report all income on tax returns. What is the probability that someone does not have this belief? The probability that someone does not believe that it is morally wrong to not report all income on tax returns is 0.16. (Type an integer or a decimal.) 1 - 0.84 = 0.16 = 16% Use the sample data and confidence level given below to complete parts (a) through (d). A research institute poll asked respondents if they felt vulnerable to identity theft. In the poll, n = 925 and x = 562 who said "yes." Use a 95 % confidence level. Find the best point estimate of the population proportion p. Find the best point estimate of the population proportion p. (Round to three decimal places as needed.) 0.608 562 / 925 = .608 Identify the value of the margin of error E. 0.031 (Round to three decimal places as needed.) 1 - 0.95 / 2 = 0.025 invNorm: .025 / 0 / 1 = -1.96 1.96 √.608 (1-.608) / 925 = .03146 Construct the confidence interval. 0.577 < p < 0.639 (Round to three decimal places as needed.) .608 - .031 = .577 .608 + .031 = .639 Write a statement that correctly interprets the confidence interval. Choose the correct answer below. A. One has 95% confidence that the interval from the lower bound to the upper bound actually does contain the true value of the population proportion. B. 95% of sample proportions will fall between the lower bound and the upper bound. C. There is a 95% chance that the true value of the population proportion will fall between the lower bound and the upper bound. D. One has 95% confidence that the sample proportion is equal to the population proportion. Which of the following values cannot be probabilities? Select all the values that cannot be probabilities. 5/3 ,  Probability value should be between 0 to 1 (both inclusive) Probability shouldn't be a negative value. Probability shouldn't be a value greater than 1. So, the following values can't be probability. To the right are the outcomes that are possible when a couple has three children. Assume that boys and girls are equally likely, so that the eight simple events are equally 1st 2nd 3rd boy boy boy boy boy girl boy girl boy boy girl girl girl boy boy girl boy girl girl girl boy girl girl girl Find the probability that when a couple has three children, there are exactly 3 boys. What is the probability of exactly 0 boys out of three children. 1/8 (type an integer or simplified fraction) 8 total ways – 1 way with 1 boy 1/8 = 0.125 The probability of a randomly selected car crashing during a year is 0.0498. If a family has three cars, find the probability that at least one of them has a crash during the year. Is there any reason why this probability might be wrong? The probability that at least one of them will crash during the year is 0.1421 1 - 0.0498 = 0.9502 1 – (0.9502) (0.9502) (0.9502) = 0.142083386 Four of the 100 digital video recorders (DVRs) in an inventory are known to be defective. What is the probability that a randomly selected item is defective? The probability is 0.04 (Type an integer or a decimal. Do not round.) 4/100 = 0.04 With a short time remaining in the day, a delivery driver has time to make deliveries at 6 locations among the 7 locations remaining. How many different routes are possible? There are 5040 possible different routes. (Simplify your answer.) 7 MATH then PRB then nPr then 6 = 5040 https://www.desmos.com/scientific nPr(7,6) There are 55 runners in a race. How many ways can the runners finish first, second, and third? There are 157410 different ways that the runners can finish first through third (Type a whole number.) https://www.desmos.com/scientific nPr(55,3) or 55 nPr 3 = 157,410 Refer to the sample data for polygraph tests shown below. If one of the test subjects is randomly selected, what is the probability that the subject is not lying? Is the result close to the probability of 0.461 for a negative test result? Did the Subject Actually Lie? No (Did Not Lie) Yes (Lied) Positive test results 12 43 Negative test results 35 12 The probability that a randomly selected polygraph test subject was not lying is .461. (Type an integer or decimal rounded to three decimal places as needed.) 12 + 35 / 12 + 43 + 35 + 12 = .461 Is the result close to the probability, rounded to three decimal places, of 0.461 for a negative test result? Yes, because there is less than a 0.050 absolute difference between the probability of a true response and the probability of a negative test result. Based on a poll, 60% of adults believe in reincarnation. Assume that 6 adults are randomly selected and find the indicated probability. Complete parts (a) through (d) below. a. What is the probability that exactly 5 of the selected adults believe in reincarnation? The probability that exactly 5 of the 6 adults believe in reincarnation is .187 (Round to three decimal places as needed.) Binompdf: Trials: 6 / P: .6 / X value: 5 0.186624 The probability that all of the selected adults believe in reincarnation is .047 (Round to three decimal places as needed.) Binompdf: Trials: 6 / P: .6 / X value: 6 0.046656 c. What is the probability that at least 5 of the selected adults believe in reincarnation? The probability that at least 5 of the selected adults believe in reincarnation is .234 (Round to three decimal places as needed.) 0.187 + 0.047 = 0.234 If 6 adults are randomly selected, is 5 a significantly high number who believe in reincarnation? A. No because the probability that 5 or more of the selected adults believe in reincarnation is greater than 0.05. B. Yes because the probability that 5 or more of the selected adults believe in reincarnation is less than 0.05. C. Yes because the probability that 5 or more of the selected adults believe in reincarnation is greater than 0.05. D. No because the probability that 5 or more of the selected adults believe in reincarnation is less than 0.05. The lengths of pregnancies are normally distributed with a mean of 267 days and a standard deviation of 15 days. a. Find the probability of a pregnancy lasting 307 days or longer. b. If the length of pregnancy is in the lowest 3%, then the baby is premature. Find the length that separates premature babies from those who are not premature a. The probability that a pregnancy will last 307 days or longer is .0038 (Round to four decimal places as needed.) 307 – 267 / 15 = 2.6666666667 (2.67) Normalcdf: ->>> -9999 / 2.67 / 0 / 1 = .9962073926 1 - .9962 = .0038 Babies who are born on or before 239 days are considered premature. (Round to the nearest integer as needed.) Area closest to 3% is .0301. invNorm: area: .0301 / 0 / 1 = -.1.879325955 (-1.88) 267 + (-1.88 x 15) = 238.8 (round to 239) The lengths of pregnancies are normally distributed with a mean of 267 days and a standard deviation of 15 days. a. Find the probability of a pregnancy lasting 308 days or longer. b. If the length of pregnancy is in the lowest 4 %, then the baby is premature. Find the length that separates premature babies from those who are not premature. The probability that a pregnancy will last 308 days or longer is .0032 (Round to four decimal places as needed.) 308 – 267 / 15 = 2.7333333333 (2.73) Normalcdf: -9999 / 2.73 / 0 / 1 = .9968332307 (.9968) 1 - .9968 = .0032 Babies who are born on or before 241 days are considered premature. (Round to the nearest integer as needed.) Area closest to 4% is .0401 invNorm: area: .0401 (4% + .01) / mu: 0 / sd: 1 -1.749526802 267 + (-1.75 x 15) = 240.75 (round to 241) Express the confidence interval (0.069,0.135) in the form of p- E < p < p+ E 0.069 < p < 0.135 (Type integers or decimals.) Refer to the accompanying data display that results from a sample of airport data speeds in Mbps. Complete parts (a) through (b) below TInterval (13.046,22.15) x = 17.598 S = 16.01712719 n = 50 What is the number of degrees of freedom that should be used for finding the critical value ta/2? df = 49 (Type a whole number.) 50 – 1 = 49 b. Find the critical value ta/2 corresponding to a 95% confidence level. ta/2 = 2.01 (Round to two decimal places as needed.) invT: .025 / Df: 49 = 2.00957 Refer to the accompanying data display that results from a sample of airport data speeds in Mbps. Complete parts (a) through (c) below. TInterval (13.046,22.15) x =17.598 Sx=16.01712719 n=50 Express the confidence interval in the format that uses the "less than" symbol. Given that the original listed data use one decimal place, round the confidence interval limits accordingly. 13.05 Mbps < μ < 22.15 Mbps (Round to two decimal places as needed.) 13.046 (rounded to 13.5) b. Identify the best point estimate of mμ and the margin of error. The point estimate of mμ is 17.60 Mbps. (Round to two decimal places as needed.) x =17.598 rounded to 17.60 The margin of error is = 4.55 Mbps. (Round to two decimal places as needed.) 17.598 – 13.046 = 4.552 In constructing the confidence interval estimate of mμ, why is it not necessary to confirm that the sample data appear to be from a population with a normal distribution? A. Because the sample is a random sample, the distribution of sample means can be treated as a normal distribution. B. Because the sample size of 50 is greater than 30, the distribution of sample means can be treated as a normal distribution. C. Because the sample standard deviation is known, the normal distribution can be used to construct the confidence interval. D. Because the population standard deviation is known, the normal distribution can be used to construct the confidence interval A magazine provided results from a poll of 1500 adults who were asked to identify their favorite pie. Among the 1500 respondents, 5 percentage points. What values do p, q, n, E, and p represent? The value of p̂ is the sample size. the margin of error. the sample proportion the population proportion. The value of q is found from evaluating 1 - p̂ the sample proportion. the sample size. the population proportion. the margin of error. The value of n is the population proportion. the sample size the margin of error. the sample proportion. found from evaluating 1 - p̂ The value of E is the population proportion the margin of error. the sample proportion the sample size The value of p is the population proportion. the margin of error. the sample proportion. the sample size. If the confidence level is 99%, what is the value of alpha? a = 0.01 (Type an integer or a decimal. Do not round.) 100% - 99% = 1% (0.01) Assume that females have pulse rates that are normally distributed with a mean of u = 73.0 beats per minute and a standard deviation of sigma equals 12.5 beats per minute. Complete parts (a) through (c) below. If 1 adult female is randomly selected, find the probability that her pulse rate is less than 80 beats per minute. The probability is .7122 (Round to four decimal places as needed.) 80 – 73 / 12.5 = .56 Normalcdf: -9999 / .56 / 0 / 1 = .7122 b. If 25 adult females are randomly selected, find the probability that they have pulse rates with a mean less than 80 beats per minute. The probability is .9974 (Round to four decimal places as needed.) 25 / 2 = 12.5 12.5 / √25 = 2.5 (80 – 73) / 2.5 = 2.8 Normalcdf: -9999 / 2.8 / 0 / 1 = .9974 c. Why can the normal distribution be used in part (b), even though the sample size does not exceed 30? A. Since the distribution is of sample means, not individuals, the distribution is a normal distribution for any sample size. B. Since the original population has a normal distribution, the distribution of sample means is a normal distribution f or any sample size. C. Since the distribution is of individuals, not sample means, the distribution is a normal distribution for any sample size. D. Since the mean pulse rate exceeds 30, the distribution of sample means is a normal distribution for any sample size. Find the sample size necessary to estimate the mean IQ score of statistics students such that it can be said with 99% confidence that the sample mean is within 6 IQ points of the true mean. Assume that sd = 15 and determine the required sample size using technology. The required sample size is 42 (Round up to the nearest integer.) 1.0 - .99 / 2 = .005 invNorm: .05 / 0 / 1 = 2.58 (round to 2 decimals) (2.58 x 15 / 6)2 = 41.6025 Would it be reasonable to sample this number of students? No, This number of IQ test scores is a fairly small number. Yes, This number of IQ test scores is a fairly small number. Yes, This number of IQ test scores is a fairly large number. No, This number of IQ test scores is a fairly large number. Sketch the region. Choose the correct graph below  The probability is .9868 (Round to four decimal places as needed.) Normalcdf: Lower: -9999 / Upper: 2.22 / Mu: 0 / Sd: 1 .9867906612 Assume that a randomly selected subject is given a bone density test. Those test scores are normally distributed with a mean of 0 and a standard deviation of 1. Find the probability that a given score is less than -0.72 and draw a sketch of the region. Sketch the region. Choose the correct graph below  The probability is 0.2358 (round to 4 decimal place) Normalcdf: Lower: (-)9999 Upper: -.72 u: 0 O: 1 0.2357624233 Determine whether the value is a discrete random variable, continuous random variable, or not a random variable.  Find the indicated z score. The graph depicts the standard normal distribution with mean 0 and standard deviation 1.  The indicated z score is 1.37 (Round to two decimal places as needed.) invNorm: Area: 0.9147 0 1 = 1.370278443 Determine whether the given procedure results in a binomial distribution (or a distribution that can be treated as binomial). If the procedure is not binomial, identify at least one requirement that is not satisfied. Nine different senators from the current U.S. Congress are randomly selected without replacement and whether or not they've served over 2 terms is recorded. A. No, because there are more than two mutually exclusive outcomes for each trial. B. No, because the experiment is not performed a fixed number of times. C. No, because the trials of the experiment are not independent and the probability of success differs from trial to trial. D. Yes, because the experiment satisfies all the criteria for a binomial experiment. Based on a survey, assume that 44% of consumers are comfortable having drones deliver their purchases. Suppose that we want to find the probability that when five consumers are randomly selected, exactly two of them are comfortable with delivery by drones. The value of n is five (5) (Type an integer or a decimal. Do not round.) The value of x is two (2) (Type an integer or a decimal. Do not round.) The value of p is 0.44 (Type an integer or a decimal. Do not round.) The value of q is 0.56 (Type an integer or a decimal. Do not round.) 1 - 0.44 = 0.56 Assume that the readings on the thermometers are normally distributed with a mean of 00 degrees and standard deviation of 1.000 C. A thermometer is randomly selected and tested. Draw a sketch and find the temperature reading corresponding to Upper P85, the 85th percentile. This is the temperature reading separating the bottom 85% from the top 15%.  The temperature for Upper P85 is approximately 1.040 (Round to two decimal places as needed.) invNorm: area: .85 / mu: 0 / sd: 1 1.03643338 Assume that a procedure yields a binomial distribution with n = 6 trials and a probability of success of p = 0.30. Use a binomial probability table to find the probability that the number of successes x is exactly 4 Click on the icon to view the binomial probabilities table. P(4) = 0.060 (Round to three decimal places as needed.) TI-84 Plus Binompdf: Trials: 6 / P: 0.30 / X value: 4 = 0.059535 round to 0.060 Ted is not particularly creative. He uses the pickup line "If I could rearrange the alphabet, I'd put U and I together. " The random variable x is the number of women Ted approaches before encountering one who reacts positively. Determine whether a probability distribution is given. If a probability distribution is given, find its mean and standard deviation. If a probability distribution is not given, identify the requirements that are not satisfied. x P(x) 0 0.001 1 0.007 2 0.031 3 0.061 Total = .01 Does the table show a probability distribution? Select all that apply. A. Yes, the table shows a probability distribution. B. No, the random variable x's number values are not associated with probabilities. C. No, the random variable x is categorical instead of numerical. D. No, the sum of all the probabilities is not equal to 1. E. No, not every probability is between 0 and 1 inclusive. Find the mean of the random variable x. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. mu = women (Round to one decimal place as needed.) B. The table does not show a probability distribution. Find the standard deviation of the random variable x. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. sd = women (Round to one decimal place as needed.) B. The table does not show a probability distribution. A _______ helps us understand the nature of the distribution of a data set. frequency distribution (A frequency distribution indicates the shape and nature of the distribution of a data set.)
Class width is found by _______.
Choose the correct answer below. A. subtracting a lower-class limit from the next consecutive lower class limit B. adding the lower class limit to the upper class limit and dividing by two C. subtracting the smallest value in the data set from the largest value in the data set D. subtracting the lower limit of one class from the upper limit of that same class
In a _______ distribution, the
frequency of a class is replaced with a proportion or percent.
relative frequency Heights of adult males are normally distributed. If a large sample of heights of adult males is randomly selected and the heights are illustrated in a histogram, what is the shape of that histogram? Longer tail to the left Longer tail to the right Bell-shaped Uniform Which of the following is NOT a value in the 5-number summary? Choose the correct answer below. Minimum Q1 Mean Median If your score on your next statistics test is converted to a z score, which of these z scores would you prefer: - 2.00, -1.00, 0, 1.00, 2.00? Why? A. The z score of -2.00 is most preferable because it is 2.00 standard deviations below the mean and would correspond to the B. The z score of 1.00 is most preferable because it is 1.00 standard deviation above the mean and would correspond to an above average test score. C. The z score of -1.00 is most preferable because it is 1.00 standard deviation below the mean and would correspond to an above average test score. D. The z score of 0 is most preferable because it corresponds to a test score equal to the mean. E. The z score of 2.00 is most preferable because it is 2.00 standard deviations above the mean and would correspond to the Methods used that summarize or describe characteristics of data are called _______ statistics. Descriptive A value at the center or middle of a data set is a(n) _______ measure of center The measure of center that is the value that occurs with the greatest frequency is the _______ Mode Identify the symbols used for each of the following: (a) sample standard deviation; (b) population standard deviation; (c) sample variance; (d) population variance. a. The symbol for sample standard deviation is S b. The symbol for population standard deviation is o c. The symbol for sample variance is S2 d. The symbol for population variance is o2 Whenever a data value is less than the mean, _______. the corresponding z-score is negative. The _________ hypothesis is a statement that the value of a population parameter is equal to some claimed value. Null Which of the following statements about correlation is true? Choose the correct answer below. A. We say that there is a negative correlation between x and y if the x-values increase as the corresponding y-values increase. B. We say that there is a positive correlation between x and y if there is no distinct pattern in the scatterplot. C. We say that there is a positive correlation between x and y if the x-values increase as the corresponding y-values decrease. D. We say that there is a positive correlation between x and y if the x-values increase as the corresponding y-values increase. The ___________ is a value used in making a decision about the null hypothesis and is found by converting the sample statistic to a score with the assumption that the null hypothesis is true. test statistic In working with two variables related by a regression equation, the _________________ in a variable is the amount that it changes when the other variable changes by exactly one unit. marginal change Which of the following statements about correlation is true? Choose the correct answer below. A. We say that there is a negative correlation between x and y if the x-values increase as the corresponding y-values increase. B. We say that there is a positive correlation between x and y if there is no distinct pattern in the scatterplot. C. We say that there is a positive correlation between x and y if the x-values increase as the corresponding y-values decrease. D. We say that there is a positive correlation between x and y if the x-values increase as the corresponding y-values increase. Which of the following is NOT a principle of probability? Choose the correct answer below. A. All events are equally likely in any probability procedure. B. The probability of any event is between 0 and 1 inclusive. C. The probability of an event that is certain to occur is 1. D. The probability of an impossible event is 0. Fill in the blank. Selections made with replacement are considered to be _______. Independent The _______ for a procedure consists of all possible simple events or all outcomes that cannot be broken down any further. Sample Space A _______ is a single value used to approximate a population parameter. point estimate The _______ is the best point estimate of the population mean Sample mean
Which of the following would be a
correct interpretation of a 99% confidence interval such as 4.1 < u
< 5.6?
Choose the correct answer below. A. There is a 99% chance that mu will fall between 4.1 and 5.6. B. It means that 99% of all data values are between 4.1 and 5.6. C. We are 99% confident that the interval from 4.1 to 5.6 actually does contain the true value of u D. It means that 99% of sample means fall between 4.1 and 5.6. Choose the correct answer below. Select all that apply. A. Sample variance used to estimate a population variance. B. Sample range used to estimate a population range. C. Sample proportion used to estimate a population proportion. D. Sample mean used to estimate a population mean. E. Sample median used to estimate a population median. F. Sample standard deviation used to estimate a population standard deviation. A. It is a normal distribution with a mean of 0 and a standard deviation of 1. B. The total area under the curve must equal 1. C. The graph is symmetric. D. The graph is uniform |
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |