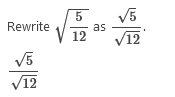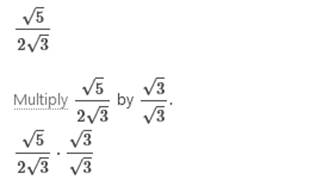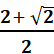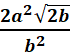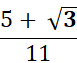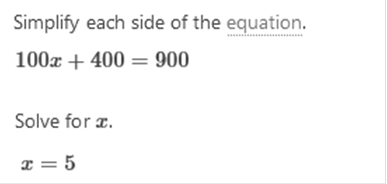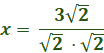Home Help & Support Search Tips Options: Case:

Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out
   Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel
Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11
Elementary and Intermediate Algebra
Chapter 9: Radicals and Rational Exponents
These Study Guides Are 100% Free

Donate Please (Help keep it free)!
This course is 100% Free. If you need more help with your class, I suggest Joining Now!


Find the root. Variables represent any real numbers. Use absolute values if necessary.

 
        6
 
Find the root. Variables represent any real numbers. Use absolute values if necessary.

 
        -5
 
We must apply the radical rule.
m = am/n
 =
-125 / 5 / 5 / 5 =
-5
Find the root. Variables represent any real numbers. Use absolute values if necessary.

2

 

        |t|

 

We must apply the radical rule.

m = am/n

2 = t2/1 = t2 – 1 = t

When the index (n) is less than an exponent of a square,

we must use the absolute value.

    |t|

Find the root. Variables represent any real numbers. Use absolute values if necessary: 3

 

    P

 

Rewrite as p3/3 and factor.

p3/3 = p

 

Find the root. Variables represent any real numbers. Use absolute values if necessary: 8

 

    |w2|

 

Rewrite as w8/4 and factor.

W8/4 = w2

Find the root. Variables represent any real numbers. Use absolute values if necessary:  12
    |w3|
 
Rewrite w12 as (w3)4
3)4

Pull terms out from under the radical, assuming positive real numbers.
w3
When the index (n) is less than an exponent of a square,
we must use the absolute value.
    |w3|

Simplify the expression. Assume all variables represent positive numbers: 82/3

 

    4

Simplify the expression.

Rewrite 8 as 23.
(23)2/3
Apply the power rule and multiply exponents, (am)n = amn.
(23)2/3

Cancel the common factor of 3.
23(2/3) = 22

Raise 2 to the power of 2 = 4

Simplify the expression. Assume all variables represent positive numbers:   4-3/2
 

 
Simplify the expression.
Rewrite 4 as 22.
Apply the power rule and multiply exponents, (am)n = amn.
(22) -3/2
Cancel the common factor of 2.
(22)-3/2 = 2-3
Raise 2 to the power of -3 = 0.125
Convert 0.125 to a fraction.

Simplify the expression. Assume all variables represent positive numbers.

 ÷

 

 

We divide this like we would without the square root.

21 / 7 = 3

Now we place it back in square root form!

Simplify the expression. Assume all variables represent positive numbers.

 ·

 

    30

 

Easiest way to do this is:

(2 · 3) · 2

Now 2 cancel each other out!

(square root to the second power is a wash!)

So, we are left with:

(3 · 2) · 5

3 · 2 - 6

6 · 5 = 30

Simplify the expression. Assume all variables represent positive numbers.

 +

 

    3

 

Since we need to simplify, we need to rewrite with common expressions,

(Like we would with a fraction and common denominators)!

 can be rewritten as 1.

.

 =  = (22)

Now we can eliminate 22 by moving 2 to the left side of the square root!

We are left with 2.

Now we can add:

 + 2

Simplify the expression. Assume all variables represent positive numbers:  +


 

Simplify each term. Multiply   by

 

 

Combine and simplify the denominator.

 

 

Combine fractions.

Simplify the numerator. Move 5 to the left of

 

 
Add the numerators likes we did above.

 

 =

 

Simplify the expression. Assume all variables represent positive numbers.

21/2 · 21/2

 

     2

 

We can rewrite the problem like so.

20.5 · 20.5

20.5 = 1

So, 1 + 1 = 2

Simplify the expression. Assume all variables represent positive numbers.

 

 

We need to find the prime numbers to solve.

72 = 2 · 2 · 2 · 3 · 3

Now we add 3 + 3 and combine 2 as the square root.

3 + 3 = 6
Simplify the expression. Assume all variables represent positive numbers:  
 

 
Simplify the denominator. (

 

A math equations with numbers and symbols Description automatically generated with medium confidence

Simplify the denominator.

A math problem with square and square symbols Description automatically generated

 

Simplify the expression. Assume all variables represent positive numbers:  

 

                            

 

 

Simplify the expression. Assume all variables represent positive numbers.

5y8

 

2ay2

 

Simplify the expression. Assume all variables represent positive numbers:  

 

 

 

 
Simplify the expression. Assume all variables represent positive numbers.

 

                                               

 

Simplify the expression. Assume all variables represent positive numbers.

3

    2m

 

Rewrite 20m3 as (2m)2⋅ (5m)

2 ⋅ (5m)

Pull terms out from under the radical.

2m

Simplify the expression. Assume all variables represent positive numbers: x1/2 · x1/4

 

    x3/4

 

Rewrite 1x1/2· 1x1/4

We can split this up.

1 · 1 = 1x = now we can drop the 1 again = x

Now we split the exponents up to form a common denominator.

 ·  +  =  +  =

x3/4

Simplify the expression. Assume all variables represent positive numbers: (9y4x1/2)1/2

 

    3y2x1/4

 

Simplify the expression. Assume all variables represent positive numbers.

7     

 

    2x2

 

Simplify the expression. Assume all variables represent positive numbers

(4 + )2

    19 + 8

 

 

Find the domain of the radical. Use interval notation:  

 

    (-∞, 4)

 

Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11
Find the domain of the radical. Use interval notation:  

 

    (-∞, ∞)

 

The domain of the expression is all real numbers except where the expression is undefined.

In this case, there is no real number that makes the expression undefined.


Interval Notation:

(−∞,∞)

 

Rationalize the denominator and simplify:  

 

 

Write the expression in the form a + bi: (3 – 2i) (4 + 5i)

 

     22 + 7i

 

Expand (3 − 2i) (4 + 5i) using the FOIL Method.
3 · 4 + 3(5i) − 2i · 4 − 2i(5i)

Simplify and combine like terms. Simplify each term.
12 + 15i − 8i + 10

Add 12 and 10.
22 + 15i − 8i

Subtract 8i from 15i.
22+7i

Write the expression in the form a + bi:   i4 – i5

 

    1 – i


Rewrite i4 as 1.
Rewrite i4 as (i2)2                      (i2)2 − i5
Rewrite i2 as −1                        −1)2−i5
Raise −1 to the power of 2      1 − i5
Factor out i4                               1 − (i4i)
Rewrite i4 as 1    
Rewrite i4 as (i2)2                       1 − ((i2)2i)
Rewrite i2as −1                           1−((−1)2i)
Raise −1 to the power of 2      −(1i)
Multiply i by 1                              1 − i


Find all real or imaginary solutions to the equation.
(x – 2)2 = 49
 
      {-5, 9}
 
Take the specified root of both sides of the equation to eliminate the exponent on the left side.
x – 2 = ±
Simplify ±
Rewrite as 72 = x – 2 = ± √72
Pull terms out from under the radical, assuming positive real numbers.
x – 2 = ± 7
The complete solution is the result of both the positive and negative portions of the solution.
First, use the positive value of the ± to find the first solution.
x – 2 = 7
Move all terms not containing x to the right side of the equation.
Add 2 to both sides of the equation.
x = 7 + 2
Add 7 and 2.
x = 9
Next, use the negative value of the ± to find the second solution.
x − 2 = −7
Move all terms not containing x to the right side of the equation.
x = −5
The complete solution is the result of both the positive and negative portions of the solution.
x = 9,−5

 

Find all real or imaginary solutions to the equation: w2/3 = 4
 
    {-8, 8}

Raise each side of the equation to the power of 3/2
to eliminate the fractional exponent on the left side.         (w2/3)3/2 = ± 43/2
Simplify the exponent. Simplify the left side.

w = ± 43/2

w = ± 22(3/2)

Now we Cancel the common factor of 2.      w = ± 22(3/2) = 23

23 = 8, so w = ± 8

Simplify the right side. w = ± 8
The complete solution is the result of both the positive and negative portions of the solution.
w = 8, −8

 

Find all real or imaginary solutions to the equation: 9y2 + 16 = 0

      {

 

Find all real or imaginary solutions to the equation:  +  = 5

 

        {5}

Find the exact length of the side of a square whose diagonal is 3 feet.

 

 

Equation we need to write

x2 + x2 = 32

Simplify

1x2 + 1x2 = 2x2

So, 2x2 = 32

Now we divide both sides by 2.

2x2 / 2 = 32 / 2

Now we square both sides…..

Now we simplify and find the answers.

 = 2

Two positive numbers differ by 11, and their square roots differ by 1. Find the numbers.
 
        25 and 36
 
Equations we need to solve
x – y = 11
 = 1
 for y in the second expression.
Add   to both sides of the second equation:
 + 1
We need to square both sides by removing the radical (from x.
 + 1
,
we can plug the value into the first expression (x – y = 11)
( + 1) – y = 11
Now we can simplify  + 1 – y = 11
 + 1 – y = 11 =
 + 1 = 11

 = 10
s by 2.
 = 5
We need to eliminate the radical (), so what we do is, we square both sides
y = 52 = The square of 5 is 25.
y = 25.
So now all we need to do is plug in the value of y and solve the rest of the equation (x – y = 11)
x – (25) = 11
We add 25 to both sides.
x = 11 + 25, so x = 36
The answer is 25 and 36
Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11


Home
 Accounting & Finance Business
 Computer Science General Studies Math Sciences
 Civics Exam
 Everything Else
 Help & Support
 Join/Cancel
 Contact Us
  Login / Log Out