Home Help & Support Search Tips Options: Case:

Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out
   Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel
Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11
Elementary and Intermediate Algebra
Chapter 8: More on Inequalities
These Study Guides Are 100% Free

Donate Please (Help keep it free)!
This course is 100% Free. If you need more help with your class, I suggest Joining Now!
Write an inequality that describes the graph below.
 
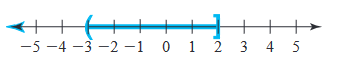A line with numbers and a blue line Description automatically generated

            -3 < x ≤ 2

No explanation needed. The graph starts at “(-3“ and ends at “2]”.

 
Write an inequality that describes the graph below.
A line with numbers and a blue line Description automatically generated

            x > 1

No explanation needed.
The graph starts at “1“ and continues in the positive direction indefinitely.


Write the solution set for the following inequality using interval notation.
x ≥ 3
 
[3, ∞)

Interval Notation: Solve for x
This means 3 is equal to x, and ∞ means all the numbers are greater than 3 indefinitely.
 

Write the solution set for the following inequality using interval notation.
                                                                                            x > 1 and x ≤ 6
 
(1, 6]
 
No explanation needed.
Interval Notation is written like so: (1,6]

Write the solution set for the following inequality using interval notation.
                                                                                             x < 5 and x > 9

            (∞, 5) U (9, ∞)

No explanation needed. Interval Notation is written like so: (∞, 5) U (9, ∞)


Write the solution set for the following inequality using interval notation.
                                                                                                          |x| < 3

            (-3, 3)
 
To find the interval for the first piece, find where the inside of the absolute value is non-negative.
x ≥ 0
In the piece where x is non-negative, remove the absolute value.
x < 3
To find the interval for the second piece, find where the inside of the absolute value is negative.
X < 0
In the piece where x is negative, remove the absolute value and multiply by −1. −x < 3
Write as a piecewise. {x < 3x ≥ 0 – x < 3x < 0
Find the intersection of x < 3 and x ≥ 0.
0 ≤ x < 3
Solve −x < 3 when x < 0.
Divide each term in −x < 3 by −1 and simplify.
X > −3
Find the intersection of x > −3 and x<0.
−3 < x < 0
Find the union of the solutions. −3<x<3
The result can be shown in multiple forms.
Inequality Form: −3 < x < 3
Interval Notation:
(−3, 3)
 

Write the solution set for the following inequality using interval notation.
                                                                                                        |x| ≥ 2

            (-∞, -2) U (2, ∞)

Write |x| ≥ 2 as a piecewise.
To find the interval for the first piece, find where the inside of the absolute value is non-negative.
X ≥ 0
In the piece where x is non-negative, remove the absolute value.
X ≥ 2
To find the interval for the second piece, find where the inside of the absolute value is negative.
X < 0
In the piece where x is negative, remove the absolute value and multiply by −1.
−x ≥ 2
Write as a piecewise.
{x ≥ 2x ≥ 0 – x ≥ 2x < 0
Find the intersection of x ≥ 2
and x ≥ 0.
X ≥ 2
Divide each term in −x ≥ 2 by −1 and simplify.
X ≤ −2
Find the union of the solutions.
X ≤ −2
or x ≥ 2
Convert the inequality to interval notation.
(−∞,−2]∪[2,∞)


Solve the inequality.
State the solution set using interval notation and graph the solution set.
2 x + 3 > 1
 
                        (-1, ∞)
 
Move all terms not containing x to the right side of the inequality.
Subtract 3 from both sides of the inequality.
2x > 1 −3
Subtract 3 from 1.
2x > −2
Divide each term in 2x > −2 by 2 and simplify.
Divide each term in 2x > −2 by 2.
2x/2 > −2/2
x > −2/2
Simplify the right side. Divide −2 by 2
x > −1
The result can be shown in multiple forms.
Inequality Form:
X > −1
Interval Notation:
(−1, ∞)
 

Solve the inequality.
State the solution set using interval notation and graph the solution set.
|m – 6|≤ 2
 
                        [4, 8]
 
Write |m − 6| ≤ 2
as a piecewise.
{m – 6 ≤ 2m ≥ 6 – m + 6 ≤ 2m < 6
Solve m − 6 ≤2 when m ≥ 6
6 ≤ m ≤ 8
Solve −m + 6 ≤ 2 when m<6
4 ≤ m < 6
Find the union of the solutions.
4 ≤ m ≤ 8
The result can be shown in multiple forms.
Inequality Form:
4 ≤ m ≤ 8
Interval Notation:
[4,8]


Solve the inequality.
State the solution set using interval notation and graph the solution set.
2| x – 3| - 5 > 15
 
        (-∞, -7) U (13, ∞)

Write 2|x − 3| − 5 > 15 as a piecewise.
{2x – 11 > 15x ≥ 3 − 2x + 1 > 15x < 3
Solve 2x – 11 > 15 for x.
X > 13
Solve −2x+1>15 for x.
X < −7
Find the union of the solutions.
X < −7
or x > 13
The result can be shown in multiple forms.
Inequality Form: x < −7 or x > 13
Interval Notation:
(−∞, −7) ∪ (13, ∞)

Solve the inequality.
State the solution set using interval notation and graph the solution set.
2 – 3(w – 1) < -2w
 
                (5, ∞)

Simplify 2−3(w−1).
−3w + 5 < −2w
Move all terms containing w to the left side of the inequality.
−w + 5 < 0
Subtract 5 from both sides of the inequality.
−w < −5
Divide each term in −w < −5 by −1 and simplify.
W > 5
The result can be shown in multiple forms.
Inequality Form: w > 5
Interval Notation: (5, ∞)
 

Solve the inequality.
State the solution set using interval notation and graph the solution set.
3x – 2 < 7 and -3x ≤ 15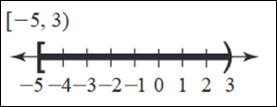
 
                A black line with numbers Description automatically generated
 
Simplify the first inequality.
x < 3
and −3x ≤ 15
Divide each term in −3x ≤ 15 by −3 and simplify.
x < 3 and x ≥ −5
The intersection consists of the elements that are contained in both intervals.
−5 ≤ x < 3
The result can be shown in multiple forms.
Inequality Form: −5 ≤ x < 3
Interval Notation: [−5,3)
 

Solve the inequality.
State the solution set using interval notation and graph the solution set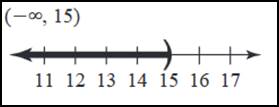
 y – 3 < 12
 
 
                      A black line with numbers and a black line Description automatically generated with medium confidence
 
 
Solve the equation or inequality.
| 2x – 7 | = -3
 
                    Ø
 
 
Solve the equation or inequality.
x – 4 > 1 or x < 12
 
            (-∞, ∞)
 
Move all terms not containing x
to the right side of the inequality.
Add 4 to both sides of the inequality.
X > 1 + 4 or x < 12
Add 1 and 4.
X > 5 or x < 12
The union consists of all the elements that are contained in each interval.
The result can be shown in multiple forms.
All real numbers:
Interval Notation:

(-∞, ∞)

Solve the equation or inequality.
3x < 0 and x – 5 > 2
 
            Ø
 
Divide each term in 3 x < 0 by 3 and simplify.
X < 0 and x – 5 > 2
Move all terms not containing x to the right side of the inequality.
x < 0 and x > 7
The intersection consists of the elements that are contained in both intervals.
No solution 

Solve the equation or inequality.
| 2x – 5 | ≤ 0
 
                {2.5}
 
Write |2x−5| ≤ 0 as a piecewise.
{2x – 5 ≤ 0 x ≥
 
−2x + 5 ≤ 0x <
Solve 2x – 5 ≤ 0 when x ≥ .
x=
Solve −2x + 5 ≤ 0 when x <.
No solution
Find the union of the solutions.
x =
The result can be shown in multiple forms.
Exact Form: x =
Decimal Form: x = 2.5
Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11

Solve the equation or inequality.
| x – 3 | < 0
 
                Ø
 
To find the interval for the first piece, find where the inside of the absolute value is non-negative.
X – 3 ≥ 0
Add 3 to both sides of the inequality. x ≥ 3
In the piece where x−3 is non-negative, remove the absolute value.
x − 3 < 0
Add 3 to both sides of the inequality.
X < 3
In the piece where x−3 is negative, remove the absolute value and multiply by −1.
−(x − 3) < 0
Write as a piecewise. {x – 3 < 0x ≥ 3 − (x−3) < 0x < 3
Simplify −(x − 3) < 0.
{x – 3 < 0x ≥ 3 – x + 3 < 0x < 3
Solve x – 3 < 0
when x ≥ 3.
Solve −x + 3 <0 when  x < 3
 
No solution


Solve the equation or inequality.
| x – 6 | > -6
 
                    (-∞, ∞)
 
Since |x−6| is always positive and −6 is negative,
|x − 6| is always greater than −6 so the inequality is always true.
All real numbers
The result can be shown in multiple forms.
All real numbers
Interval Notation:
(−∞,∞)

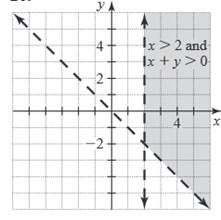
    Sketch the graph of the inequality x > 2 and x + y > 0.

 

A graph of x and y axis Description automatically generated

Graph x > 2. Graph x + y > 0.
Subtract x from both sides of the inequality.
y > −x
Use the slope-intercept form to find the slope and y-intercept.
The slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.
y = mx + b

Find the values of m and b using the form y = mx + b.
m = −1, b = 0

The slope of the line is the value of m, and the y-intercept is the value of b.
Slope: −1
y - intercept: (0,0)

Graph a dashed line, then shade the area above the boundary line since y is greater than −x.
y > −x

Plot each graph on the same coordinate system.
x > 2

x + y > 0

A graph of x and y axis Description automatically generated

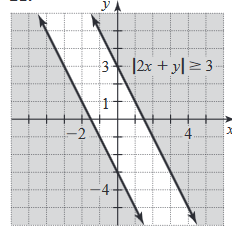
Sketch the graph of the inequality |2x + y| ≥ 3.

A graph of a function Description automatically generated

A graph of x and y with red lines Description automatically generated

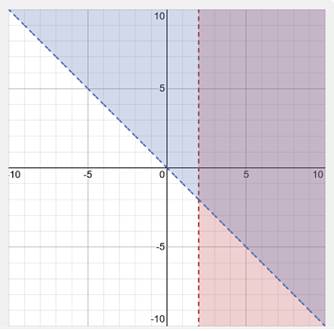
Sketch the graph of the inequality x + y > 1 or x – y < 2.

A graph of x and y axis Description automatically generated

Graph x + y > 1.
Write in y = mx + b form.
y > − x + 1

Use the slope-intercept form to find the slope and y-intercept.
Slope: −1
y-intercept: (0,1)

Graph a dashed line, then shade the area above the boundary line
since y is greater than −x + 1.
y > −x + 1

Graph x – y < 2 - Write in y = mx + b form.
y > x − 2

Use the slope-intercept form to find the slope and y-intercept.
Slope: 1
y-intercept: (0, −2)

Graph a dashed line, then shade the area above the boundary line since y is greater than x−2.
y > x − 2

Plot each graph on the same coordinate system.
x + y > 1
x – y < 2

A graph of x and y axis Description automatically generated

Al and Brenda do the same job, but their annual salaries differ by more than $3000,
Assume that Al makes $28,000 per year and write an absolute value inequality to describe this situation.
What are the possibilities for Brenda’s salary?

| x – 28,000 | > 3,000 where x is Brenda’s salary.

Brenda makes more than $31,000 or less than $25,000.


Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11


Home
 Accounting & Finance Business
 Computer Science General Studies Math Sciences
 Civics Exam
 Everything Else
 Help & Support
 Join/Cancel
 Contact Us
  Login / Log Out