|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Intermediate
Algebra Chapter 1 2 3 4 5 6 7 8 9 10 11
Elementary and Intermediate Algebra
Chapter 6: Rational Expressions
These Study Guides Are 100% Free
 Donate Please (Help keep it free)! This course is 100% Free. If you need more help with your class, I suggest Joining Now!
Perform the indicated operation. Write the answer in lowest terms.
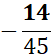 Find common denominator of 15 & 9 = 45 (Set up equation).  =  = 
Perform the indicated operation. Write the answer in lowest terms.
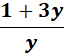  Find common denominator, set up equation & solve. In this case, we need to add a variable to 3 (which in fraction form is  ) =  Please note, we cannot add 1 + 3y because they are not like terms.
Perform the indicated operation. Write the answer in lowest terms.
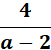  Find common denominator, set up equation & solve.  Rearrange in order.  Combine the numerators over the common denominator.  =  Divide two negative values of 1 which results in a positive value.  Perform the indicated operation. Write the answer in lowest terms.
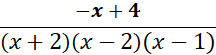 Write as a fraction with a common denominator, multiply by 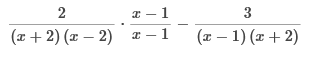  Write as a fraction with a common denominator, multiply by   Write each expression with a common denominator of (x + 2) (x − 2) (x − 1), by multiplying each by an appropriate factor of 1. 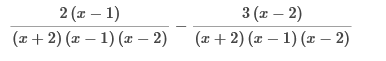 Combine the numerators over the common denominator. Simplify the numerator. 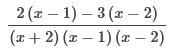 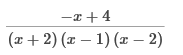 Simplify with factoring out.  Perform the indicated operation. Write the answer in lowest terms.
 · 
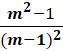 Simplify the numerator and simplify terms. 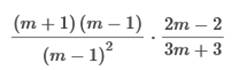 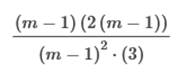 Cancel the common factors. Cancel the common factor of m − 1.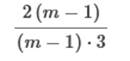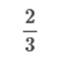  
Perform the indicated operation. Write the answer in lowest terms.
 ÷ 
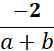 To divide by a fraction, multiply by its reciprocal (or swap the second fraction around). ·  Now we cancel the common factor of 3 (we will need to divide the 6 in the 2nd fraction).  ·  (a – b) · 𝟐𝒂𝟐− 𝒃𝟐 Since both terms in the 2nd fraction are perfect squares, factor using the difference of squares formula, (a – b) ·  Now we can cancel out (a – b) since they are on both sides.  =  Perform the indicated operation. Write the answer in lowest terms.  ·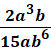 
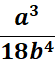 Combine. 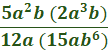 Multiply a2 by a3 (only) by adding the exponents. 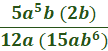 Multiply b by b (only) 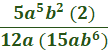 Cancel the common factor of 5 and 15 (so we need to divide 15 by 5). 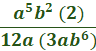 Cancel the common factor of a5 and a2. 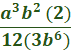 Cancel the common factor of 2 and 12 (divide 12 by ) 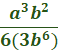 We can now cancel the common factor of b2 and b6.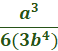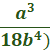   
Simplify the
complex fraction
  First, we find common denominators for each set. *We could find common denominators for all which would be 30, however, beginners should learn this way first!  =  =   =  =   which is a little more manageable for
beginners. multiply by its reciprocal(or swap the second fraction around like we did above).  =   -220 / 55 = -4 -165 / 55 = -3 The answer is 
Simplify the
complex fraction
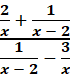
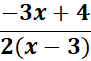 Multiply the numerator and denominator of the fraction by x(x−2). 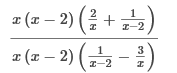 Apply the distributive property. 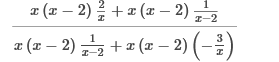 Simplify by cancelling. 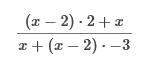 Simplify the numerator. 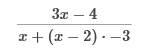 Simplify the denominator and Simplify with factoring out.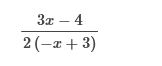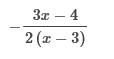   
 First, we need to rewrite this to solve for 0.  Then we add  to both sides of the
equation. Find the LCD of the terms in the equation which is 5x. Multiply each term by 5x to eliminate the fractions. 15 = 7x Last, we divide both sides by 7 and solve the equation.   =  2, 3 First we Find the LCD of the terms in the equation which is 2x (x − 1). Then we Multiply 2x (x – 1) to eliminate the fractions. 2x2 − 6x + 6 = x2 – x Now we move all terms containing x to the left side of the equation. 2x2 - x2 = x2, and − 6x + x = -5x x2 − 5x + 6 = 0 We have done this already. We write the factored form using these integers. (x − 3) (x − 2) = 0 x – 3 = 0 = We add 3 to both sides: x = 3 x − 2 = 0 = We add 2 to both sides: x = 2
Solve the equation
 = 
12 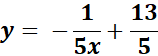 =  for y. Multiply both sides by x + 2 and simplify y – 3 =  Move all terms not containing y to the right side of the equation. All we need to do is add 3 to  3 + =  - =  - =   round them up and bring them back. it takes Norman 18 minutes to do the same job. How long would it take them working together to complete the roundup? 7.2 minutes x / 12 + x / 18 = 1 x / 2 + x / 3 = 6 3x + 2x = 36 5x = 36 x = 36/5 7 minutes 12 sec.
Brenda and her husband Randy bicycled cross-country together. One morning,
Brenda rode 30 miles. By traveling only 5 miles per hour faster and putting in one more hour, Randy covered twice the distance Brenda covered. What was the speed of each cyclist? Brenda 15 mph and Randy 20 mph or Brenda 10 mph and Randy 15 mph Brenda traveled 30 mi Randy traveled 60 mi  + 1 =  x(x + 5) ·  + 1 · x(x + 5) = x(x + 5) ·  Cancel the denominators, leaving 30(x+5) + x(x+5) = 60x 30x + 150 + x2 + 5x – 60x = 0 Combine as a quadratic equation: x2 – 25x + 150 = 0 Factors to: (x - 10) (x - 15) = 0 Two good solutions for B's speed x = 10 mph x = 15 mph
For
a certain time period the ratio of the dollar value of
exports to the dollar value of imports for the United States was 2 to 3.
If the value of exports during that time period was 48 billion dollars, then what was the value of imports? 72 billion 2 / 48:3 / x 2x = 144 x = $72b
What numbers
cannot be used for x in the following expression?
 -1, 1 What numbers cannot be used for x in the following expression?   What numbers cannot be used for x in the following expression?  0 |
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |