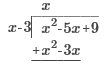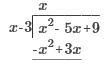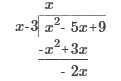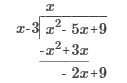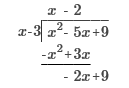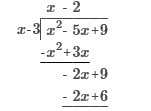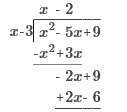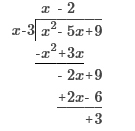Home Help & Support Search Tips Options: Case:

Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out
   Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel
Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11
Elementary and Intermediate Algebra
Chapter 4: Exponents and Polynomials
These Study Guides Are 100% Free

Donate Please (Help keep it free)!
This course is 100% Free. If you need more help with your class, I suggest Joining Now!


Use the rule of exponents to solve -5x3 ⋅ 7x5
 
-358
 
-5 ⋅ 7 = -35

3 ⋅ 5 = 3 + 5 = 8

Use the rule of exponents to solve 3x3y ⋅ (2xy4)2
 
12x5y9
 




 
 
Use the rule of exponents to solve -4a6b5 ÷ (2a5b)
 
-2ab4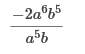
 
A number and a line Description automatically generated with medium confidence


 
 
Use the rule of exponents to solve 3x-2 ⋅ 5x7
 
15x5
 
3x ⋅ 5x = 15x
-2 – 7 = 5
 
 
Use the rule of exponents to solve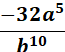
 

 
 
-2a5 = -32a5
b2 + 5 = b10
 
 
Use the rule of exponents to solve 
 

 
 =
 
 =
 
 = 0
 
   =
 
Use the rule of exponents to solve 
 

 
We use the negative exponent rule.
 =  =
 
 
Use the rule of exponents to solve (-2x-6y)3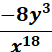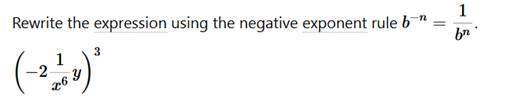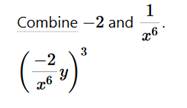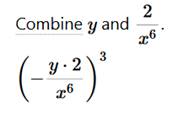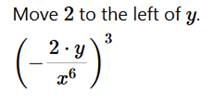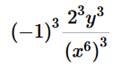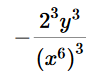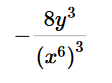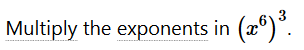
 

 
A black text on a white background Description automatically generated
A math equations on a white background Description automatically generatedA white background with black text Description automatically generated
A math equations on a white background Description automatically generatedA math problem with numbers Description automatically generated with medium confidence

A number and numbers on a white background Description automatically generatedA black and white math equation Description automatically generated with medium confidenceA black and white image of numbers Description automatically generated
A black text with black letters Description automatically generated

 
Convert 5,433,000 to scientific notation:       

5.433 ⋅ 106
 
First, we will put a decimal point at the end of number 5433000.
To write number 5433000. in scientific notation we need to move the decimal point
from its current location (black dot) to the new position (red dot).
5.433000.
So, we need to move decimal point 6 places to the right.
This means that the power of 10 will be positive 6. Now we have that the
Number part = 5.433000 (which can be written as 5.433) and Exponent part = 6
5.433 ⋅ 106

Convert 0.0000065 to scientific notation.

 
6.5 ⋅ 10-6
 
To write number 0.0000065 in scientific notation we need to move the decimal point
from its current location (black dot) to the new position (red dot).
0.000006.5
So, we need to move the decimal point 6 places to the left.
This means that the power of 10 will be negative 6.
Now we know that the base = 6.5 and Exponent  = -6
So, the solution is:
6.5 ⋅ 10-6
 
Convert 3.2 ⋅ 103 to standard notation.
 
3,200
 
103 = 1,000
3.2 ⋅ 1,000 = 3,200
 
 Convert 8 ⋅ 10-5 to standard notation.
 
0.00008
 
10-5     =  = 0.00001
 
0.00001 ⋅ 8 = 0.00008
 
Convert 3.5 billion to standard notation.
 
3,500,000,000
 
 
Convert 12 trillion to standard notation.
 
12,000,000,000,000
 
 
Perform the computation by converting (80,000) (0.000006) to scientific notation.
 
4.8 ⋅ 10-1
 
(80,000) (0.000006) = 0.48
0.48 = 4.8 ⋅ 10-1
 
Perform the operation: (7x3 – x2 – 6) + (5x2 + 2x – 5)
 
7x3 + 4x2 + 2x – 11
 
We need to combine like terms. If some have no like term,
then that will stand alone. We move from left to right.
Like Term or terms means base numbers, which have the same variable and exponent.
(Example: 7x3
7 is the base number, x is the variable, and 3 is the exponent.)
 
(7x3 – x2 – 6) + (5x2 + 2x – 5)
7x3 stands alone.
-x2 + 5x2 = -1x2 + 5x2 = 4x2 (notice that that variable and exponent remains the same, and only the base changes)
2x stands alone.
-6 + -5 = -11
Now we put the equation back in proper order of operation.
7x3 + 4x2 + 2x – 11
Perform the operation: (x2 – 3x – 6) - (2x2 + 6x – 7)
 
-x2 – 9x + 1
 
This will be the same, except we subtract.
Remember, we group in like terms, and change only the base numbers unless there is no like term.
 
      x2 – 3x –  6 -  (2x2 + 6x – 7)
(the 7 becomes positive in this case because we are multiplying 2 negatives)
      -x2 - 9x + 1
 
Note: whenever a negative is before an equation inside paratheses,
we must multiply each Expression by -1.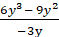
 
Perform the operation:
 
-2y2 + 3y
 
It may be easier to rewrite this operation like so.
(6y3 – 9y2) ÷ -3y
We do this to remind us that we need to divide the ENTIRE numerator (top) by the denominator (bottom).
So, in this case, we need to divide both expressions above the line by the expression below the line.
If there were two expressions below the line, we would not, for various reasons, but we will not get into that now.
So, this is rather simple now that we have rewritten the operation.
(6y3 – 9y2) ÷ -3y
We divide 6y3 by -3y (it will become negative, and we need to subtract 1 from the exponent because -3y is -3y1).
6y3 ÷ -3y = 6 ÷ -2 = -2, and the exponent 3 – 1 = 2 = -2y2
Next, – 9y2 ÷ -3y = 3y
Now we put the equation back together.
-2y2 + 3y
Perform the operation: (x - 2) ÷ (2 - x)
 
-1
 
This is exactly what I was talking about above.
This could be written like the operation above.
 

 
Since there are 2 expressions as the denominator, we need to divide like terms.
The variables will be subtracted and cancelled, because in essence,
they have exponents with the same value.
 
x1 - x1 = 0
-2 ÷ 2 = -1
 
The answer is -1

Perform the operation: 3x2(5x3 – 7x2 + 4x – 1)

 
15x5 – 21x4 + 12x3 – 3x2
 
3 ⋅ 5x2 x3
+          3 ⋅ −7x2x2
+          3 ⋅ 4x2x
−                  3x2
=             15x5 – 21x4 + 12x3 – 3x2
 
Find the product of (x + 5) (x – 2)
 
x2 + 3x – 10
 
x ⋅ x
+          x ⋅ −2
+          5x
+          5 ⋅ −2
=          x2 + 3x – 10

 

Find the product of (3a - 7) (2a + 5)
 
6a2 + a – 35
 
3a (2a)
+          3a ⋅ 5 − 7(2a)
–          7 ⋅ 5
=          6a2 + a – 35
 
 
Find the product of (a - 7)2
 
a2 – 14a + 49
 
(a – 7) (a – 7)
a ⋅ a
+          a ⋅ −7
–          7a −7 ⋅ −7
a2 – 14a + 49
 
 
Find the product of (4x + 3y)2
 
16x2 + 24xy + 9y2
 
Rewrite:
(4x+3y) (4x+3y)
 4x(4x)
+          4x(3y)
+          3y(4x)
+          3y(3y)
=          16x2 + 24xy + 9y2
 
 
Find the product of (b – 3) (b + 3)
 
b2 – 9
 
b ⋅ b
+          b ⋅ 3
–          3b
–          3 ⋅ 3
=          b2 – 9 
Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11
Find the product of (3t2 - 7) (3t2 + 7)
 
9t4 – 49
 
3t2 ⋅ 3t2
+          3t2 ⋅ 7
–          7 ⋅ 3t2
–          7 ⋅ 7
 
 
Find the product of (4x2 - 3) (x2 + 2)
 
4x4 + 5x2 - 6
 
4x2x2
+        4x2 ⋅ 2
–          3x2
–          3 ⋅ 2
=        4x4 + 5x2 - 6
 
Find the product of (x - 2) (x + 3) (x - 4)
 
x3 – 3x2 – 10x + 24
 
x ⋅ x + x ⋅ 3 − 2x −2 ⋅ 3 ⋅ (x−4)
=          (x2 + x − 6) (x − 4)
x2x
+          x2 ⋅ −4
+          x ⋅ x
+          x ⋅ −4
–          6x – 6 ⋅ −4
x3 – 3x2 – 10x + 24

Write the expression


2 +

 

A white paper with black text Description automatically generated A screenshot of a computer Description automatically generated

Write the expression

x – 5 +


A white paper with black text Description automatically generated 

A screenshot of a white page Description automatically generated

A close-up of a white background Description automatically generated

 

Find the value of the polynomial x3 – 5x + 2, when x = 3.

14

(3)3 – 5(3) + 2
27 – 15 + 2
12 + 2 = 14

Suppose that P(x) = x2 – 5x + 2: Find P(0) and P(3).

2, -4
 
P (0) x2 – 5x + 2 = (0)2 – 5(0) + 2 = 0 – 0 + 2 = 2
P (3) = (3)2 – 5(3) + 2 = 9 – 15 + 2 = -4

Find the quotient and remainder when x2 – 5x + 9 is divided by x – 3.

x – 2, 3

Set up the polynomials to be divided. If there is not a term for every exponent, insert one with a value of 0.
 
Divide the highest order term in the dividend x2 by the highest order term in divisor x.
 
Multiply the new quotient term by the divisor.
 
 
The expression needs to be subtracted from the dividend, so change all the signs in x2−3x
 
 
After changing the signs, add the last dividend from the multiplied polynomial to find the new dividend.
 
 
 
Pull the next terms from the original dividend down into the current dividend.
 
 
Divide the highest order term in the dividend −2x by the highest order term in divisor x.
 
 

 
Multiply the new quotient term by the divisor.
 
 
 
 
The expression needs to be subtracted from the dividend, so change all the signs in −2x+6
 
 
 
 
After changing the signs, add the last dividend from the multiplied polynomial to find the new dividend.
 
 
 
 
The final answer is the quotient plus the remainder over the divisor.

A math equations on a white background Description automatically generated

A math problem with numbers and symbols Description automatically generated

Subtract 3x2 – 4x -9 from x2 – 3x + 6.

 
-2x2 + x + 15
 
x2 – 3x2                        =  -2x2
 -3x + -(-4) = -3x + 4x   =   x
6 + -(-9) = 6 + 9            =   15
Put the equation back together.
-2x2 + x + 15 

The width of a pool table is x feet and the length is 4 feet.

a.     Find polynomials A(x) and P(x) that represent the area of the pool table.
b.     Find A(4) and P(4).
 
a.    A(x) = x2 + 4x
b.    P(x) = 4x + 8
a.    A(4) = 32 ft2
b.    P(4) = 24 ft
 
A(4) = (4)2 + 4(4) = 16 + 16   =        32
P(4) = 4(4) + 8 = 16 + 8         =        24
If a manufacturer charges q dollars each for football then he can sell 3,000 – 150q footballs per week.
Find a polynomial R(q) that represents the revenue if the price is $8 for each football.
 
R(q) = -150q2 + 3000q
$14,400
 
-150(8)2 + 3000(8)
-9,600 + 24,000 = 14,400
Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11


Home
 Accounting & Finance Business
 Computer Science General Studies Math Sciences
 Civics Exam
 Everything Else
 Help & Support
 Join/Cancel
 Contact Us
  Login / Log Out