|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Intermediate
Algebra Chapter 1 2 3 4 5 6 7 8 9 10 11
Elementary and Intermediate Algebra Chapter 3: Linear Equations in Two Variables and Their Graphs
These Study Guides Are 100% Free
 Donate Please (Help keep it free)! This course is 100% Free. If you need more help with your class, I suggest Joining Now! Name the
quadrant or axis on which (-2, 7) lies.
Answer: Quadrant II 
Name the
quadrant or axis on which (-
Answer: x-axis
Name the quadrant or axis
on which (-
Answer: Quadrant IV 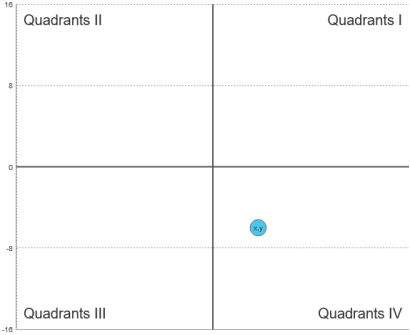
Name the quadrant or axis
on which (0, 1785) lies.
Answer: y-axis Find the slope of the line through the pair of points (3, 3) and (4, 4). Answer: m = 1 y2 - y1 / x2 – x1
Find the slope of the line
through the pair of points (-2, -3) and (4, -8).
Answer: y2 - y1 / x2 – x1 -8 – (-3) / 4 – (-2) = -5/6 Find the slope of the line y = 3x – 5 Answer: 3 The slope-intercept form is y = mx + b m is the slope and b is the y-intercept. b y = 3x – 5 The slope is given! Find the slope of the line y = 3 Answer: 0 Since y is given, and x is not represented, the slope = 0. The slope-intercept form is y = mx + b y = mx + b m is the slope and b is the y-intercept. y = (0)x + b Find the slope of the line x = 5 Answer: Undefined “x = 5” is a vertical line, and y is not given, therefore the slope is undefined. Find the slope of the line 2x – 3y = 4. Answer: Rewrite in slope-intercept form by solving for y. We are only looking for the slope-intercept, so we move y alone. – 3y = 4 – 2x Now we divide 4 and -2x by -3 y = - Now we out the equation into y = mx + b form y = 2/3 is the slope! Write the equation of the line. Give the answer in slope -intercept format. The line through (0, 3) with slope -1/2 Answer: Consider the Gradient Form of a linear function: y = mx + c m is the gradient of the graph. and c is the constant term (effectively the y intercept) If we substitute m= and c = 3 (the y intercept of the graph) we get the equation: Write the equation of the line. Give the answer in slope -intercept format. The line through (-1, -2) with slope We know the slope is -2 = -2 = - -2 + Now we rewrite in y = mx + b form. (Remember the slope we saved above Sketch the graph of the equation y = 1/2x – 3 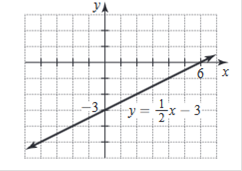
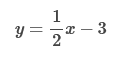
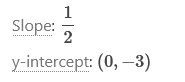 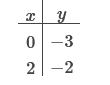 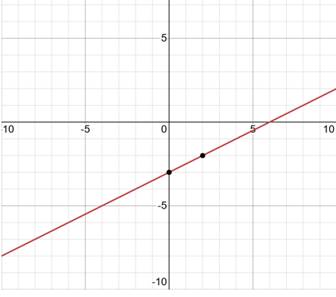
Sketch the graph of the equation 2x – 3y = 6 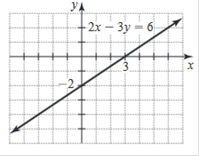
Subtract 2x from both sides of the equation. −3y = 6 − 2x Divide each term in −3y = 6 − 2x by −3 and simplify. Rewrite in slope-intercept form. 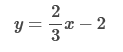 The slope of the line is the value of m, and the y-intercept is the value of b.  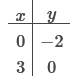 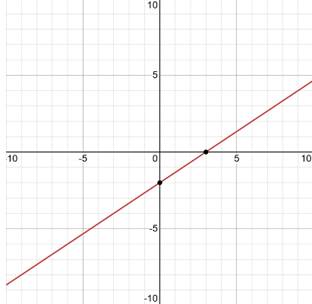
Julie's mail-order CD club charges a shipping and handling fee of $2.50 plus $0.75 per CD for each order shipped. Write the shipping and handling fee S in terms of the number n of CDs in the order. Answer: S = 0.75n + 2.50 The price in dollars p for a supreme pizza is determined by the function p(n) = 0.50n + 12.75, where n is the number of toppings. a. Find p (1), p (3), and p (10) Answer: $13.25, $14.25, $17.75 0.50(1) + 12.75 = 13.25 0.50(3) + 12.75 = 14.25 0.50(10) + 12.75 = 17.75 b. Find the number of toppings on a pizza for which the price is $16.25. Answer: 7 Toppings Write the equation > 16.25 – 12.75 / .50 16.25 – 12.75 = 3.50 3.50 / .50 = 7 A 10-ounce soft drink sells for 50 cents, and a 16-ounce soft drink sells for 68 cents. The price P is determined from the volume v of the cup by a linear equation. a) Find the linear function. Use function notation. P(v) = 3v + 20 68 - 50 = m (16 - 10) 18 = 6m (Slope) m = 18 / 6 Slope = 3 y - 50 = 3(x - 10) y - 50 = 3x - 30 y = 3x - 30 + 50 y = 3x + 20 b) Find the price of a 20-ounce soft drink. 80 cents P(v) = 3v + 20 P = 3(20) + 20 P = 60 + 20 P = 80 c) Find the number of ounces in a soft drink for which the price is $1.64. 48 ounces This was very tricky to solve because we are dealing in CENTS and the question threw me off for a few moments, so, we need to convert $1.64 into cents first!!! 1.64 = 164 cents Now we write the equation. 164 = 3(x) + 20 Subtract 20 from both sides (we can swap sides also). 3x = 164 – 20 3x = 144 Now we divide. x = 48 The demand for tickets to a play can be modeled by the equation d = 1000 – 20p, where d is the number of tickets sold and p is the price per ticket in dollars. a) How many tickets will be sold at $10 per ticket? Answer: 800 d = 1000 – 20(10) 1000 – 200 = 800 b) Find the intercepts and interpret them. Answer: (0, 1000) (50, 0) d = 1000-20p At p = 0, d = 1000 The d-intercept is (0,1000) (p,d) is the order d = 1000-20p at d = 0, p = 50 The p-intercept is (50,0) c) Find the intercepts and interpret them. Answer: -20 The slope is -20 tickets sold per dollar price. Raising the price $1 causes 20 fewer tickets to be sold.
The price P for a
watermelon varies directly with its weight w.
a) Write a formula for this variation. Answer: P = kw b) If the price of a 30-pound watermelon is $4.20, then what is the price of a 20-pound watermelon? Answer: $2.80 4.2 = k(30) k = 4.2/30 k = 2.1/15 k = 0.7/5 k = 7/50 So the Equation is P = (7/50)w then what is the price of a 20-pound watermelon? P = (7/50)(20) P = 14/5 Price = $2.80 The number n of days that Jerry spends on the road is inversely proportional to the amount A of his sales for the previous month. a) Write a formula for this variation. Answer: N = k/A b) Jerry spent 15 days on the road in February because his January sales amount was $75,000. If his August sales amount is $60,000, Answer: 18.75 days 15 = k / 75,000 k = 75,000(15) = 1,125,000 n = 1125000 a = 60,000 so, n = 1,125,000 / 60,000 = 18.75 c) Does his road time increase or decrease as his sales increase? Decreases
The cost C for installing
ceramic floor tile in a rectangular room varies jointly with the length L and width
W of the room.
a) Write a formula for this variation. Answer: C = kLW b) The cost is $400 for a room that is 8 feet by 10 feet. What is the cost for a room that is 11 feet by 14 feet? Answer: $770 x = 400 / 8 / 10 x = 5 11 x 14 x 5 = 770  Answer: B  Answer: C  Answer: A 5 / 6 = 8.3333333333  Answer: C 61 ÷ 100 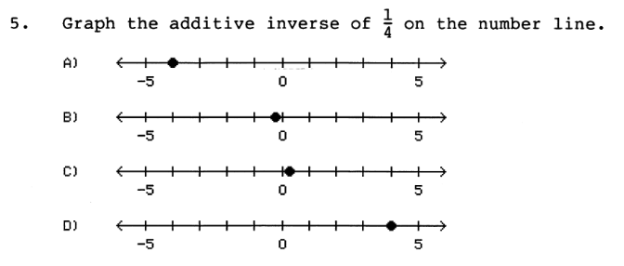 Answer: B ¼ is less than 1, so it will be plotted on the left side. 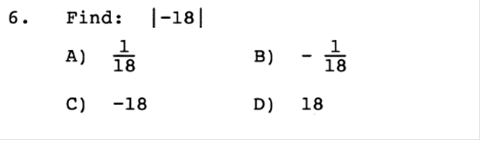 Answer: D The absolute value of either a negative or positive number is always positive. You will learn later when an absolute value is used in an equation, the answer can be either positive or negative. 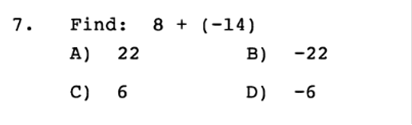 Answer: D When a negative number is multiplied by a positive number, the value is always negative, such as +(-14) = -14. For this equation, you would first find the value of +(-14) = -14, then factor. 8 + -14 = -6  Answer: B We would need to add both negative numbers, and when two negative numbers are added, the value remains negative. -18 + -5 = -23  Answer: B Since all the numbers are being multiplied together, they can be swapped or moved around because the answer will remain the same.  Answer: C If there is no negative sign on the left side of parentheses, then it is assumed as a positive. +(-5) would remain a negative value. Then we multiply -2 x -5 = 10. When two negative numbers are multiplied, the value is then positive. 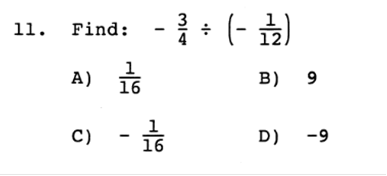 Answer: B The same rule applies with this equation. If there is no negative sign on the left side of parentheses, then it is assumed as a positive. +(-1/12) = -1/12 then the value would remain negative. Then we divide -3/4 by -1/12 When two negative numbers are multiplied, the value is then positive. In this case we would MULTIPLY -3 · -12 and move the value on top = Then we would MULTIPLY and move the value on the bottom = 36 ÷ 4 Then we divide 36 by 4 to simplify = 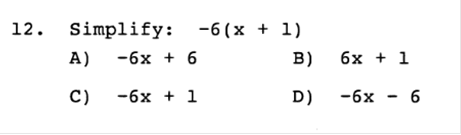 Answer: D We would multiply both numbers in parentheses by -6. Since both numbers are in parentheses, they will both have negative values. If there is no number on the left side of x, then the value is assumed as 1. -6 · 1x + -6 · 1 = -6x - 6 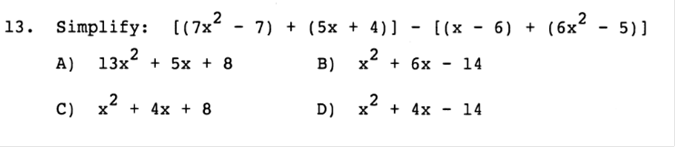 Answer: C Since we are adding and subtracting all the values, we would group each expression, in order, by the value of the exponents (example: x2 would be grouped with another value of x2). We would start with the highest value, being 7x2 and move to the right adding or subtracting in order. When exponents are added, the value of the exponent remains the same. For Example, x2 + x2 would be 2x2. First we need to convert the right side since the bracket is negative –[…] -[(x - 6) + (6x2 – 5)] = (-x + 6) + (-6x2 + 5) 7x2 - 6x2 = x2 5x – x = 4x -7 + 4 + 6 +5 = -3 + 6 + 5 = 3 + 5 = 8 Now we put the equation back together starting with the highest value of x. x2 + 4x +8  Answer: A This value would be positive, because the base of the value is negative, and the exponent or power is an EVEN Number and will be multiplied an even number of times. If it was odd, then it would be a negative number. The TI84 Plus will do this for you. -4 · -4 · -4 · -4 = 625 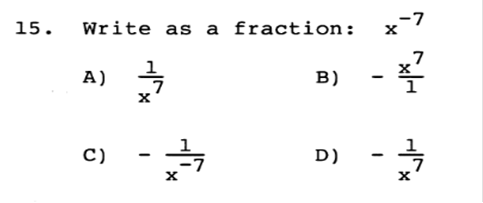 Answer: A The rule for fractional exponents is 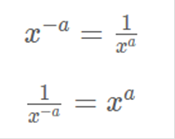  Answer: D This would be the same rule as above except you would multiply the exponents because you are moving the exponent up. When you multiply a, you add the exponents, but you must first use the rule from above. So, first you divide terms. 44 ÷ 11 = 4 Then (x4) · (x(6)) = x4 + 6 = x10 Then put the equation back together. 4x10 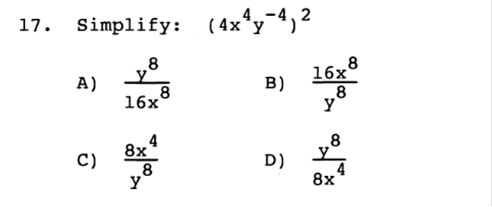 Answer: B 4x4 · 4x4 = 16x8 y-4 · y-4 = y8  Answer: D 4.6 · 9 = 41.4 107 · 10-9 = 10-2  Answer: B -6 · 6 = -36 -6 · 7 = -42 -36 – 42 = -78 -78 + 8 = -70 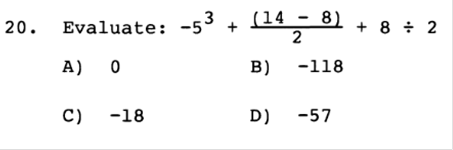 Answer: B -53 = -125 and 14 – 8 ÷ 2 = 3 -125 + 3 = -122 -122 + (8 ÷2) = -118 |
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |