Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11

---

Elementary and Intermediate Algebra
Chapter 11: Functions

---

---

    Yes

The domain is the set of all "x" values
the range is set of all "y" values in a set of ordered pairs.

Domian for this set:          0, 9, 4
Range for this set:          5 (repeated values do not need to be listed)

When looking at a set of ordered pairs, find the domain by listing all the x values from the relation.
Find the range by listing all the y values from the ordered pairs.
Repeated values within the domain or range don't have to be listed more than once.
For a relation to be a function, each x must correspond with only one y value.
If an x value has more than one y-value associate with it (example {(4, 1), (4,2)},
the x-value of 4 has a y-value of 1 and 2, so this set of ordered pairs is not a function.

If each x-value corresponds with only one y-value, then the relation is a function.

Let f (x) = -2x + 5. Find f (-3).

    11

Simply plug in the value (-3)
-2(-3) + 5
-2 · -3 = 6
6 + 5 = 11

Find the domain and range of the function y = .

 
    Domain    Range    [7, ∞), [0, ∞)

Set the radicand in √x−7 greater than or equal to 0 to find where the expression is defined.
x − 7 ≥ 0 Add 7 to both sides of the inequality.        x ≥ 7
The domain is all values of x that make the expression defined.
Interval Notation:              [7, ∞)
Set-Builder Notation:       {x |x ≥ 7}
The range is the set of all valid y values.
Interval Notation:  [0, ∞)
Set-Builder Notation: { y | y ≥ 0}
Determine the domain and range.
Domain: [7, ∞), {x | x ≥ 7}
Range: [0, ∞), {y | y ≥ 0}

A mail-order firm charges its customers a shipping and handling fee of $3.00 plus $0.50 per pound
for each order shipped. Express the shipping and handling fee S as a function of the weight of the order n.

 
    S = 3 + 0.50n

No explanation needed.

If a ball is tossed into the air from height of 6 feet with a velocity of 32 feet per second,
then its altitude at time t (in seconds) can be described by the function,
A(t)=-16t² + 32t + 6 Find the altitude of the ball at 2 seconds.

    6 feet

Since the application (word problem) uses A & t, we will do the same.
We need to write the equation first and plug in the value 2 for t.
A(t) = -16t² + 32t + 6
A(2) = -16(2)² + 32(2) + 6
Now let’s simplify the right side…
-16(2)² + 32(2) + 6 = -16 · 4 + 64 + 6 = -64 + 70 = 6
Since we plugged in the value of 2 into A(t), we do not need to factor anymore.
The answers is 6 (feet)

Sketch the graph pf the function or relation and state the domain range. f(x) = x + 1

     (-∞, ∞), (-∞, ∞)

First, we must rewrite the function as an equation.
Since we plot x,y on a graph, we will replace f(x) with y.
y =  + 1

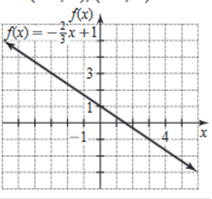
Now we use the slope-intercept form to find the slope and y-intercept. y = mx + b

m = , and b = 1

x: 0 | 3          y: 1 | -1
Graph the line using the slope and the y-intercept, or the points.       Slope: −
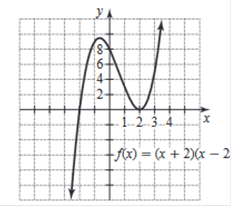
y-intercept: (0, 1)

Graph the function. Identify all intercepts. f(x) = (x + 2) (x – 2)²

    (-2, 0), (2, 0), (0, 8)

Find the point at x = −1
f(x) = ((-1) + 2) (-1 – 2)2
(-3)2 = (1) (9) = 9    y = 9
Find the point at x = 0.
Replace the variable x with 0 in the expression.
F (0) = (0) ((0) −2) 2 + 2((0) −2)2
Simplify the result. Simplify each term.
f(0) = 0 + 8    Add 0 and 8.            f(0) = 8
The final answer is 8.
Convert 8 to decimal. y = 8
Find the point at    x = 1.              y = 3
Find the point at    x = 2.              y = 0
Find the point at                x = 3               y = 5

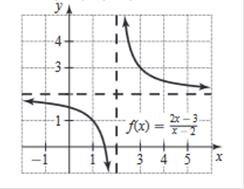
Graph the function. Identify all intercepts. f(x) =

          (, 0) (0, )

Find where the expression  is undefined.       x=2

Consider the rational function
R(x) = axⁿ / bx^m where ⁿ is the degree of the numerator and ^m is the degree of the denominator.

1. If n < m, then the x-axis, y = 0, is the horizontal asymptote.
2. If n = m, then the horizontal asymptote is the line y = ab.
3. If n > m, then there is no horizontal asymptote (there is an oblique asymptote).

Find n and m.          n = 1               m = 1
Since n = m, the horizontal asymptote is the line y = ab where a = 2 and b = 1.
y = 2

There is no oblique asymptote because the degree of the numerator is less than,
or equal to the degree of the denominator.
No Oblique Asymptotes - This is the set of all asymptotes
Vertical Asymptotes: x = 2
Horizontal Asymptotes: y = 2

No Oblique Asymptotes

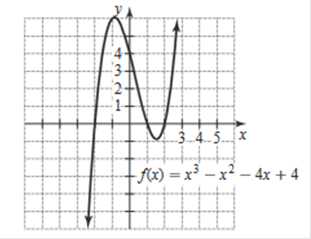
Graph the function. Identify all intercepts. f(x) = x³ – x² - 4x + 4

    x-intercepts     (-2, 0), (1, 0), (2, 0)
    y-intercepts     (0, 4),

Find the x-intercepts.

To find the x-intercept(s), substitute in 0 for y and solve for x.
0 = x³ − x²− 4x + 4

Solve the equation - Rewrite the equation as x³ −x² − 4x + 4 = 0.
x³ − x² − 4x + 4 = 0

Factor the left side of the equation. Factor out the greatest common factor from each group.
x²(x − 1) − 4(x − 1) = 0

Factor the polynomial by factoring out the greatest common factor, x−1.
(x − 1) (x² − 4) = 0   Rewrite 4 as 2².
(x−1) (x² −2²) = 0

Factor. Since both terms are perfect squares, factor using the difference of squares formula,
a² − b2 = (a + b) (a − b) where a=x and b=2.              (x − 1) ((x + 2)(x − 2)) = 0

Remove unnecessary parentheses.    (x − 1)(x + 2)(x − 2) = 0      x = 1, −2, 2
x-intercept(s) in point form.      x-intercept(s): (1, 0),(−2, 0),(2, 0)

Find the y-intercepts. To find the y-intercept(s), substitute in 0 for x and solve for y.
y = (0)³ − (0)² – 4 · 0 + 4

Solve the equation. Remove parentheses.
y = 0³ − (0)² – 4 · 0 + 4        Remove parentheses. y = 0³ − 0² −4 · 0 + 4

Remove parentheses.     y = (0)³ − (0)² −4 · 0 + 4
Simplify (0)³−(0)²−4 · 0 + 4.
Simplify each term.          y = 0 + 0 + 0 + 4
Simplify by adding numbers.     Add 0 and 0.
y = 0 + 0 + 4              Add 0 and 0.            y = 0 + 4
Add 0 and 4.            y = 4

y-intercept(s) in point form.      y-intercept(s): (0,4)
List the intersections.      x-intercept(s): (1, 0), (−2, 0),(2, 0)

y-intercept(s): (0,4)

Solve the inequality. State the solution set using interval notation. x³ + 4x² – 32x > 0

    (-8, 0) ∪ (4, ∞)

Convert the inequality to an equation.
x³+ 4x²− 32x = 0

Factor the left side of the equation.   x(x−4) (x+8) = 0
If any individual factor on the left side of the equation is equal to 0,

the entire expression will be equal to 0.
x = 0               x – 4 = 0                    x + 8 = 0

Set x equal to 0.     x = 0
Set x – 4 equal to 0 and solve for x. x = 4
Set x + 8 equal to 0 and solve for x.
x = −8

The final solution is all the values that make x(x−4) (x+8) = 0    true.
x = 0, 4, −8

Use each root to create test intervals.
x < −8             −8 < x < 0          0 < x < 4            x > 4

Choose a test value from each interval and plug this value into the original inequality
to determine which intervals satisfy the inequality.

x < −8             False
−8 < x < 0      True
0 < x < 4        False
x > 4               True

The solution consists of all of the true intervals.
−8 < x < 0 or x > 4
The result can be shown in multiple forms.
Inequality Form:                −8 < x < 0 or x > 4
Interval Notation:             (−8, 0) ∪ (4, ∞)

Solve the inequality. State the solution set using interval notation.  ≤ 0

(∞, -5) ∪ (0, 5)

 
Find all the values where the expression switches from negative to positive
by setting each factor equal to 0 and solving.
x = 0               x²−25=0
Add 25 to both sides of the equation.            x² = 25
Take the specified root of both sides of the equation to eliminate the exponent on the left side.
x = ± √25        Simplify ± √25 = x = ± 5
The complete solution is the result of both the positive and negative portions of the solution.
x = 5, −5
Solve for each factor to find the values where the absolute value expression goes from negative to positive.
x = 0                x = 5, −5
Consolidate the solutions.         x = 0, 5, −5
Find the domain of
 (−∞, −5) ∪ (−5, 5) ∪ (5, ∞)
Use each root to create test intervals.

x < −5             −5 < x < 0                  0 < x < 5        x > 5
Choose a test value from each interval and plug this value into the
original inequality to determine which intervals satisfy the inequality.

x < −5             True

−5 < x < 0      False

0 < x <5         True

x > 5   False

The solution consists of all of the true intervals.

x < −5 or 0 ≤ x <5

The result can be shown in multiple forms.
Inequality Form:    x<−5 or 0 ≤ x < 5
Interval Notation:  (−∞, −5) U [0, 5)

Let f(x) = -2x + 5 and g(x) = x² + 4. Find f(-3)

    11

Since we are looking for f, and there is no value for g(x), we simply

Plug in the value of -3      -2(-3) + 5.

-2 · -3 = 6

6 + 5 = 11

Let f(x) = x – 7 and g(x) = x²

Write the following function as a composition of function, using f and g, H(x) = x² – 2

H = f ∘ g

Let f(x) = x – 7 and g(x) = x² - Write the following function as a composition of function, using f and g
W(x) = x² – 14x + 49

W = g ∘ f

Determine whether the function is invertible. If it is invertible, find the inverse.
                                                                                                {(2, 3), (4, 3), (1, 5)}

    Not Invertible

Not invertible because y is repeated in the set (3 and 3)!

Determine whether the function is invertible. If it is invertible, find the inverse.
                                                                                                {(2, 3), (3, 4), (4, 5)}

    {(3, 2), (4, 3), (5, 4)}

Simply swap the numbers, in order.
Inverse of (2, 3) = (3, 2)
Inverse of (4, 3) = (3, 4)
Inverse of (5, 4) = (4, 5)

Find the inverse of the function: f(x) = x – 5

    f^-1 (x) = x + 5

To find the inverse function, swap x and y., and solve the resulting equation for y.
This means that the inverse is the reflection of the function over the line y = x.
If the initial function is not one-to-one, then there will be more than one inverse.
So, swap the variables: y = x − 5y becomes x = y − 5x.
Now, solve the equation x = y − 5x for y.

y = x + 5

    f^-1 (x) =

 

Find the inverse of the function: f(x) =

    f^-1 (x) = x³ – 9

Move the index (3) to the square 3 over x, and multiply 9 by -1

x¹⁽³⁾ + 9(-1) = x³ + 9

Find the inverse of the function: f(x) =

f^-1 (x) =

 

Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11