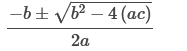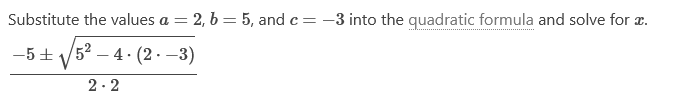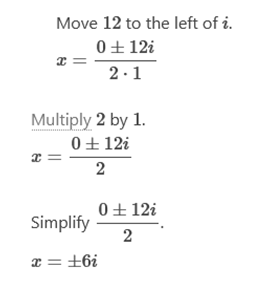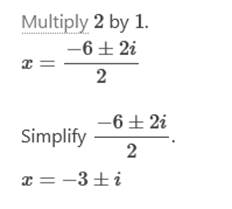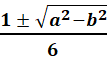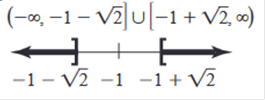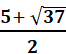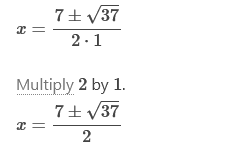Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11

---

Elementary and Intermediate Algebra
Chapter 10: Quadratic Equations, Functions, and Inequalities

---

2x² – 3x + 2 = 0

 
      -7

0 real solutions

 

Explanation

The value of b² – 4ac is called the “discriminant” of a quadratic equation.

The discriminant of a quadratic is the expression inside the radical of the quadratic formula.

b² − 4(ac)

 a       b      c

2x² – 3x + 2 = 0

 

Notice the positions of a, b, & c in the formula first!!!

b² − 4(ac) is the formula.

Substitute in the values of a, b, and c.

(−3)² − 4(2 ⋅ 2)

Evaluate the result to find the discriminant.

(−3)² = 9

− 4(2 ⋅ 2) = -16

Subtract 16 from 9.

9 – 16 = -7

−7

Since the discriminant, -7, is negative, there are 0 real solutions.

If the discriminant, (b² − 4(ac)) > 0, it has 2 Real Solutions

If the discriminant, (b² − 4(ac)) = 0, it has 1 Real Solutions

If the discriminant, (b² − 4(ac)) < 0, it has 1 Real Solutions

Calculate the value of b² – 4ac, and state how many real solutions the equation has.

-3x² + 5x – 1 = 0

 

13

2 real solutions

 

Explanation

The discriminant of a quadratic is the expression inside the radical of the quadratic formula.

b²−4(ac)

Substitute in the values of a, b, and c.

5²           − 4(−3 ⋅ −1)

25       −      12

Subtract 12 – 25 =

13

13 > 0, so, it has 2 Real Solutions

Calculate the value of b² – 4ac, and state how many real solutions the equation has.

4x² – 4x + 1 = 0

 

0

1 real solutions

 

Explanation

b²−4(ac)

Substitute in the values of a, b, and c.

(−4)² −4(4 ⋅ 1)

(−4)² = 16

−4(4 ⋅ 1) = -16

16 − 16

0

0 = 0, so, it has 1 Real Solutions

 

Solve by using the quadratic formula: 2x² + 5x – 3 = 0

-3,

 

Check Answer

http://coursesavior.com/free/quadratic-equation-solver/

 

Explanation

Use the quadratic formula to find the solutions.

 

Solve by using the quadratic formula: x² + 6x + 6 = 0

 

x = -3

 

Simplify the numerator.

Solve by competing the square: x² + 10x + 25 = 0

 

x = -5

 

Check Answer

http://coursesavior.com/free/quadratic-equation-solver/

 

Explanation

Solve by competing the square: 2x² + x – 6 = 0

 

x = -2,  (or 1.5)

 

Check Answer

http://coursesavior.com/free/quadratic-equation-solver/

 

Explanation

Solve by any method: x(x + 1) = 12

 

x = 3, −4

 

Explanation

Move all terms to the left side of the equation and simplify.

Simplify the left side.

x² + x = 12

Subtract 12 from both sides of the equation.

x² + x – 12 = 0

Simplify. Simplify the numerator.

The final answer is the combination of both solutions.

x = 3, −4

Solve by any method.

a⁴ – 5a² + 4 = 0

 

a = ,

 

Explanation
Rewrite a4 as (a2)².
(a²)² − 5a² + 4 = 0
Let u=a². Substitute u for all occurrences of a².
u² − 5u + 4 = 0
Factor u²− 5u + 4 using the AC method.
Consider the form x² + bx + c.
Find a pair of integers whose product is c and whose sum is b.
In this case, whose product is 4 and whose sum is −5.

−4, −1

Write the factored form using these integers.
(u − 4) (u − 1) = 0
Replace all occurrences of u with a².
(a² − 4) (a² − 1) = 0
Rewrite 4 as 2². (a² − 2²) (a² − 1) = 0

Since both terms are perfect squares, factor using the difference of squares formula,
a² − b² = (a + b) (a − b) where a = a and b = 2.
(a + 2) (a−2) ( a² − 1) = 0
Rewrite 1 as 12.  (a + 2) (a − 2) ( a² − 12) = 0.
Factor (a + 2)(a − 2)(a + 1)(a − 1)=0
If any individual factor on the left side of the equation is equal to 0,
the entire expression will be equal to 0.

a + 2 = 0, a – 2 = 0, a + 1 = 0, a – 1 = 0

Set a + 2 equal to 0 and solve for a.      a = −2
Set a −2 equal to 0 and solve for a.       a = 2
Set a + 1 equal to 0 and solve for a.       a = −1
Set a – 1 equal to 0 and solve for a.       a = 1

The final solution is all the values that make (a + 2) (a − 2)(a + 1)(a − 1) = 0 true.
a = −2, 2, −1, 1

Solve by any method: x – 2 - 8 + 15 = 0

 

11, 27

 

Explanation
Solve for −8 .
Add −2 and 15.       x−8 + 13 = 0
Move all terms not containing −8 to the right side of the equation.
−8 = −x −13

To remove the radical on the left side of the equation, square both sides of the equation.
(−8 ² = (−x −13)²

Simplify each side of the equation.     64x – 128 = x² + 26x + 169

Solve for x - Since x is on the right side of the equation,

switch the sides so it is on the left side of the equation.  x² + 26x + 169 = 64x − 128

Move all terms containing x to the left side of the equation.     x² − 38x + 169 = −128

Add 128 to both sides of the equation.          x² − 38x + 169 + 128 = 0

Add 169 and 128.              x² − 38x + 297 = 0

Factor x² − 38x + 297 using the AC method.  (x−27) (x−11) = 0

If any individual factor on the left side of the equation is equal to 0,

the entire expression will be equal to 0.        x – 27 = 0      x – 11 = 0

Set x – 27 equal to 0 and solve for x.               x = 27

Set x – 11 equal to 0 and solve for x. x = 11

The final solution is all the values that make           (x−27) (x−11)= 0 =             x = 27, 11

Find the complex solution to the quadratic equation x² + 36 = 0

 

6i

 

Explanation

Simplify. Simplify the numerator.

Find the complex solution to the quadratic equation x² + 6x + 10 = 0

 

x = −3 ± i

 

Simplify. Simplify the numerator.

 

Find the complex solution to the quadratic equation 3x² - x + 1 = 0

                        x =

 

Explanation

 

Simplify. Simplify the numerator.

Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11

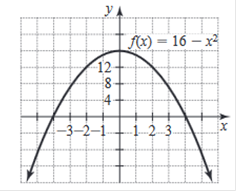
Graph the parabola. Identify the vertex, intercepts, and the maximum or minimum y-value: f(x) = 16 – x²

 

Vertex (0, 16)

Intercepts (0, 16), (-4, 0), (4, 0)

Maximum value 16

 

Explanation
Vertex (0, 16) solution
Rewrite the equation in vertex form. Reorder 16 and −x². y = −x² + 16
Complete the square for −x² + 16.        −(x + 0)² + 16
Set y equal to the new right side.        y = −(x + 0)² + 16
Use the vertex form, y=a(x−h)² + k, to determine the values of a, h, and k.
a = −1             h = 0               k = 16
Find the vertex (h, k).
(0, 16)

Intercepts (0, 16), (-4, 0), (4, 0) solutions
To find the x-intercept(s), substitute in 0 for y and solve for x.  0 = 16 −x²
Solve the equation. Rewrite the equation as 16 − x² = 0              16 −x² = 0
Subtract 16 from both sides of the equation.          −x² = −16
Divide each term in −x² = −16 by −1 and simplify.  x² = 16
Take the specified root of both sides of the equation to eliminate the exponent on the left side.
x = ±  > Simplify > x = ± 4
The solution is the result of both the + and - portions of the solution. x = 4, −4
x-intercept(s) in point form        x-intercept(s): (4, 0), (−4, 0)
To find the y-intercept(s), substitute in 0 for x and solve for y.               y = 16 − (0)²
y-intercept(s): (0, 16)

List the intersections. x-intercept(s): (4, 0), (−4, 0) y-intercept(s): (0,16)
Maximum y-value solution.

The maximum of a quadratic function occurs at x =

If a is negative the maximum value of the function is f ().

fmax^x = ax² + bx + c occurs at x =

We must find the value of x =

Substitute in the values of a and b     

Now we move the negative one from the denominator of x = −(−1 ⋅ 0)

Rewrite −1 ⋅ 0 as −0 x = − (−0), so x = 0

We are looking for the maximum y value, and found x, so now we:

Evaluate f (0).

Replace the variable x with 0 in the expression.

f (0) = 16 −(0)²

minimum y-value = 16

Graph

We use the information above to graph the parabola.

We use a, h, and k. we have all of them already.

Glance up and you will see 2a, so a = -1.

h and k are (0, 16), so

Graph the parabola. Identify the vertex, intercepts, and the maximum or minimum y-value: g(x) = x² – 3x

 

x-intercept(s): (0,0), (3,0)

y-intercept(s): (0,0)

 

Explanation
Intercepts
To find the x-intercept(s), substitute in 0 for y and solve for x.
0 = x² − 3x
Solve the equation
Rewrite the equation as x² − 3x = 0.
Factor x out of x² − 3x.     x(x − 3) = 0
If any individual factor on the left side of the equation is equal to 0, the entire expression will be equal to 0.
x = 0               x – 3 = 0            Set x equal to 0                x= 0

Set x−3 equal to 0 and solve for x.
Set x−3 equal to 0        x – 3 = 0

Add 3 to both sides of the equation        x=3
The final solution is all the values that make x (x − 3) = 0 true.
x = 0, 3 x-intercept(s) in point form. x-intercept(s): (0,0),(3,0)

Find the y-intercepts.
To find the y-intercept(s), substitute in 0 for x and solve for y.
Solve the equation.    y = (0)2 - 3 ⋅ 0        y = 0
y-intercept(s) in point form.
y-intercept(s): (0,0)
List the intersections.
x-intercept(s): (0,0), (3,0)
y-intercept(s): (0,0)

Write a quadratic equation that has each given pair of solutions: -4, 6

 

x² – 2x – 24 = 0

 

Explanation
x = −4 and x = 6 are the two real distinct solutions for the quadratic equation,
which means that x + 4 and x − 6 are the factors of the quadratic equation.
So, (x + 4) (x − 6) = 0
Now we expand (x + 4)(x − 6) using the FOIL Method.

Apply the distributive property.          x (x − 6) + 4(x − 6) = 0

Apply the distributive property.          x . x + x . −6 + 4(x − 6) = 0
Apply the distributive property.          x . x + x . −6 + 4x + 4 . −6 = 0

Simplify and combine like terms. Simplify each term.      x² − 6x + 4x – 24 = 0

Add −6x and 4x.     x² − 2x – 24 = 0

Write a quadratic equation that has each given pair of solutions: -5i, 5i

x² + 25 = 0

 

x = −5i and x = 5i are the two real distinct solutions for the quadratic equation,
which means that x−(−5i) and x − 5i are the factors of the quadratic equation.
(x + 5i) (x − 5i) = 0
Expand (x + 5i)(x − 5i) using the FOIL Method.
x . x + x(−5i) +5ix + 5i(−5i) = 0
Simplify terms. Combine the opposite terms in x . x + x(−5i) + 5ix + 5i(−5i).
x . x + 5i(−5i) = 0
Simplify each term.                      x² + 25 = 0

Solve the inequality. State and graph the solution set: w² + 3w < 18

 

(6, -3)

 

Explanation
Convert the inequality to an equation.                      w² + 3w = 18
Subtract 18 from both sides of the equation.          w² + 3w − 18 = 0
Factor w² + 3w – 18 using the AC method.                (w−3) (w+6)=0
If any individual factor on the left side of the equation is equal to 0,
the entire expression will be equal to 0.                 w – 3 = 0       w + 6 = 0
Set w – 3 equal to 0 and solve for w.                          w = 3
Set w + 6 equal to 0 and solve for w.                          w = −6
The final solution is all the values that make (w−3) (w+6) = 0 true.     w = 3, −6
Use each root to create test intervals.                       w < − 6          −6 < w < 3     w > 3
Choose a test value from each interval and plug this value into the original inequality
to determine which intervals satisfy the inequality.
w < − 6 False              −6 < w < 3     True               w > 3  False

The solution consists of all of the true intervals.   −6 < w < 3
The result can be shown in multiple forms.
Inequality Form:                −6 < w < 3
Interval Notation:             (−6, 3)

Solve the inequality. State and graph the solution set: x² + 2x ≥ 1.

 

 

                  

 

Explanation

Solve the inequality. State and graph the solution set: x² – 6x + 13 > 0

 

  (−∞,∞)

 

Explanation

Convert the inequality to an equation. x² − 6x + 13 = 0

Simplify.

x = 3 ± 2i
Identify the leading coefficient.
The leading term in a polynomial is the term with the highest degree:         x²
The leading coefficient in a polynomial is the coefficient of the leading term         1
Since there are no real x-intercepts and the leading coefficient is positive,
the parabola opens up and x² − 6x + 13 is always greater than 0.
All real numbers
The result can be shown in multiple forms.
All real numbers
Interval Notation:
(−∞,∞)

Solve the inequality. State and graph the solution set: x – x² ≥ 4

 

O (no solution)

 

Explanation
Subtract 4 from both sides of the inequality: x − x² – 4 ≥ 0
Convert the inequality to an equation. x − x² – 4 = 0
Use the quadratic formula to find the solutions.

Simplify, Identify the leading coefficient.
Reorder x and −x²  −x² + x
The leading term in a polynomial is the term with the highest degree.          −x²
The leading coefficient in a polynomial is the coefficient of the leading term. −1
Since there are no real x-intercepts and the leading coefficient is negative,
the parabola opens down and x − x2 is always less than 0.
No solution

Find the exact solution to the problem.

A new computer can process a company’s monthly payroll in 1 hour less time than the old computer.

To really save time, the manager used both computers and finished the payroll in 3 hours.

How long would it take the new computer to do the payroll by itself?

 

 or 5.5 hours

 

Explanation

1/ (x-1) + 1 / x = 1/3 find the LCM x(x-1).
(x + x - 1) / x(x - 1) = 1/3 combine like terms.
(2x - 1)/(x² - x) = 1/3 cross multiply.
x² - x=3(2x-1)
x²  -x = 6x - 3
x² – x - 6x + 3 = 0
x² - 7x + 3 = 0

Simplify the numerator.

Decimal Form:
x = 6.54138126
6.54 – 1 = 5.54 hrs.

Find the exact solution to the problem.

The height in feet for a ball thrown upward at 48 feet per second is given by

s(t) = -16t² + 48t, where t is the time in seconds after the ball is tossed.

What is the maximum height that the ball will reach?

 

36 feet

 

Explanation

Intermediate Algebra Chapter     1    2   3   4   5   6   7   8   9   10   11