|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Intermediate
Algebra Chapter 1 2 3 4 5 6 7 8 9 10 11
Elementary and Intermediate Algebra Chapter 1: Real Numbers and Their Properties
These Study Guides Are 100% Free
 Donate Please (Help keep it free)! This course is 100% Free. If you need more help with your class, I suggest Joining Now! Find the prime factorization of 756. 22 · 33 · 71 42 · 33 · 21 52 · 73 · 81 52 · 33 · 31 The number 756 is composite and therefore it will have prime factors. Now let us learn how to calculate the prime factors of 756. The first step is to divide the number 756 with the smallest prime factor, here it is 2. We keep dividing until it gives a non-zero remainder. 756 ÷ 2 = 378 378 ÷ 2 = 189 Further dividing 189 by 2 gives a non-zero remainder. So, we stop the process and continue dividing the number 189 by the next smallest prime factor. We stop ultimately if the next prime factor doesn't exist or when we can't divide any further. So, the prime factorization of 756 can be written as 22 × 33 × 71 where 2, 3, 7 are prime. Combine like terms: 5n + 8 + 2n – 1. 7n + 7 Explanation 5n + 2n = 7n 8 – 1 = 7 7n + 7 Evaluate when x= −2 and y= 3: |3x−4y|6 6|−6−12y| Explanation Simplify each term. Multiply 3 by −2. |−6−4y ⋅ 3|⋅6 Multiply 3 by −4. |−6−12y|⋅ 6 Move 6 to the left of |−6−12y| 6|−6−12y| Translate to an algebraic expression and simplify: eleven less than negative eight -8 – 11 = -19 Translate to an algebraic expression and simplify: the difference of −8 and −3, increased by 5 −8 − (−3) + 5 = 0 No explanation needed… Please match my answers to the task. Dushko has nickels and pennies in his pocket. The number of pennies is seven less than four times the number of nickels. Let n represent the number of nickels. Write an expression for the number of pennies. 4n - 7 No explanation needed… Please match my answer to the task. Round 28.1458 to the nearest: Hundredth 28.15 Explanation Rounding to the nearest hundredth means the rounding of any decimal number to its nearest hundredth value. In decimal, hundredth means 1/100 or 0.01. When the number to the right of the nearest hundredth is equal to 4 or less, the value of that number stays the same. When the number to the right of the nearest hundredth is equal to 5 or more, then the value of the number will increase by 1. Example: 1.111 = 1.114 When asked to round to the nearest hundredth, the third 1 would stay the same. 1.11 Example: 1.115 – 1.119 When asked to round to the nearest hundredth, the third 1 would increase by 1. 1.12 Round 28.1458 to the nearest: Thousandth 28.146 When the number to the right of the nearest thousandth is equal to 4 or less, the value of that number stays the same. When the number to the right of the nearest thousandth is equal to 5 or more, then the value of the number will increase by 1. Convert the expression 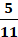 to a decimal to a decimal
0.4545454545 Explanation Simply divide 5 by 11. The question does not ask to round, so we won’t! In College Mathematics Courses, decimals are almost always in the 0.0… form  TI84 Plus Simply divide 5 by 11 1.15 to a percent 115 percent or 115% Explanation Simply multiply the number (1.15) by 100. If there were 4 or more digits, then a decimal would be included, unless you are asked to round. 1. Locate 3/5, 2.8, and 5/2, on a number line. 
In the following exercise, simplify the expression: 8 + 3[6 − 3(5 − 2)] −42 -43 Explanation First, innermost parentheses (on the left) are calculated. -3(5 – 2) = -15 + 6 Now we place -15 + 6 inside the brackets and remove -3(5 – 2) and simplify even further. 8 + next step > 3[6 – 15 + 6] −42 3 · 6 = 18 3 · -15 = -45 3 · 6 = 18 Now we can set up the final expression and simplify from left to right. 8 + 18 – 45 + 18 −42 26 – 45 + 18 – 42 -19 + 18 – 42 -1 – 42 = -43 In the following exercise, simplify the expression: −(4−9) −(9−5) 1 Explanation When there’s a negative to the left of parentheses, all the numbers inside the parentheses are multiplied by -1. In Algebra, innermost parentheses (on the left) are calculated first. -1 · 4 = -4 -1 · -9 = 9 -1 · 9 = -9 -1 · -5 = 5 Now must simplify innermost (left) to outermost (right). Notice above that I placed The expressions up and down in that order. -4 + 9 – 9 + 5 = 1  The TI84 Plus However, the - on the left of (4-9) is a negative, not a minus. The negative is below the number 3 and the minus is below the x. In the following exercise, simplify the expression. 56 ÷ (−8) + (−27) ÷ (−3) 2 Explanation With this problem, we can divide first (always from left to right). 56 ÷ -8 = -7 -27 ÷ -3 = 9 Now we simply add -7 and 9 -7 + 9 = 2 *Please note, in Algebra, the order of operation does not matter with multiplication and division. However, multiplication must always be done first when there is any value, including a negative sign, to the left of parentheses. parentheses (…) are done first. brackets […] are done second (there will always be parentheses when there are brackets) braces {…} are done third. (there will always be brackets and parentheses when there are braces) vertical bars |…| are done last (vertical bars are absolute values. We will get to that next)! | is last { is third [ is second ( is first  The TI84 Plus Remember, (-8), (-27), and (-3) are NEGATIVES not minuses. In the following exercise, simplify the expression. 16 − 2| 3(1 − 4) −(8 − 5) | -8 Explanation Since this expression has vertical bars, or absolute values, we will factor parentheses first, however, we must SIMPLIFY the expression inside parentheses first. I know this is confusing, because normally we would multiply the value on the left of parentheses by all the values inside parentheses. We do not do that with absolute values. You should not see this much in Algebra; however, it is good to practice just in case. So here we go. 16 − 2| 3(1 − 4) − (8 − 5) | First, we will simply the values in parentheses 3(1 − 4) − (8 − 5) 3(-3) – (3) We can plug the values back in. 16 − 2|3(-3) – (3)| Now we will multiply the value on the left of parentheses by all the values inside parentheses. 3 · -3 = -9 -1 · 3 = -3 Now we are left with 16 − 2|-9 – 3| Still, we need to simplify the express inside the vertical bars. | - 9 – 3| = |-12| *The absolute value is the distance between a number and zero. The distance between −12 and 0 = 12 Now we need to multiply the value on the left of vertical bars by all the values inside the vertical bars. – 2(12) = -24 Now we are left with 16 – 24 which = -8  The TI84 Plus However, you need to use the Absolute Value Bars located in the catalog. so, you enter 16 - 2 then 2nd then catalog (located on the bottom left on top of 0). So, now you should have 16 - 2 | | The TI 84 Plus will place both bars for you. You simply add the rest of the equation between the bars 16 − 2| 3(1 − 4) −(8 − 5) | . You will need to move the cursor over past the last absolute value bar (closing bar) and press enter! In the following exercise, simplify the expression. −5 + 2(−3)2 − 9 -26 Explanation 2(-3)2 = -12 Now we plug in -12 with the rest and simplify −5 – 12 – 9 = -26  The TI84 Plus Remember, -5 and (−3) are NEGATIVES not minuses. The TI84 Plus will give you an error unless you use the negative key! In the following exercise, simplify the expression. Explanation This is how I simplify fractions. You can use whatever method you want, but this always works for me. Now I know 180 and 204 are divisible by 2, so we can start there. 180 / 2 = 90 204 / 2 = 102 90 and 102 are divisible by 2, so 90 / 2 = 45 102 / 2 = 51 Now I know 45 and 52 are divisible by 3, so 45 / 3 = 15 51 / 3 = 17 That’s as far as we can go, so we put the fraction back together.  The TI84 Plus Simply divide 180 by 204 (180 / 204) and press enter. You will get a a long decimal answer .88235...... That is no prblem. All you do is: Press MATH 1:>Frac will be highlighted. Press Enter. Ans>Frac will appear. Press Enter again and you will get the fraction answer 15 / 17 In the following exercise, simplify the expression. Explanation The common denominator of 18 and 12 is 36. So, we need to set up both fractions. We will need to multiply 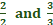 because
36 / 18 = 2 and 12 / 36 = 3 because
36 / 18 = 2 and 12 / 36 = 3
The fraction form of 2 is Don’t rush this. If you are not familiar, take some time to absorb it, because You will be working with fractions a lot during this course! Now we can add the numerators. *The denominators (bottom of the fractions) stay the same when adding fractions!  The TI84 Plus (7/8) + (5/12) Enter MATH 1:>Frac Enter Ans>Frac Enter In the following exercise, simplify the expression: Explanation It is up to you on how to simplify this expression. If you are a beginner, you can flip the second fraction and multiply straight across. *you can also multiply the first numerator by the second denominator and place The value as the numerator of the answer and vice versa. I will set it up by flipping the second fraction. Now we simplify even further.  The TI84 Plus (4/5) / (12/25) Enter MATH 1:>Frac Enter Ans>Frac Enter In the following exercise, simplify the expression: 47 Explanation Simply cancel 47 -11.5 Explanation -4.8 + -6.7 = -11.5 -65.4 Explanation You can use a calculator for this one! I suggest the TI-84 Plus! Use the Minus Sign. Not the Negative Sign! -50.568 Explanation You can use a calculator for this one! I suggest the TI-84 Plus! Use the NEGATIVE sign for this because a negative number comes first! The Negative sign is not the same as the Minus (subtract) sign on the TI 84 Plus. The Negative sign will be on the bottom right of the keyboard (-). The Minus sign is - . -160 Explanation You can use a calculator for this one! I suggest the TI-84 Plus! Use the NEGATIVE sign for this because a negative number comes first! The Negative sign is not the same as the Minus (subtract) sign on the TI 84 Plus. The Negative sign will be on the bottom right of the keyboard (-). The Minus sign is - . 11i Explanation The TI 84 Plus will not simplify this expression. So, we would need to do it the long way. First, we rewrite the expression as NOW, we can find the square root of 121 with the TI84 plus. The square root of 121 = 11. Now we need to rewrite when The answer is 11i -x – 5y Explanation This we simply simplify like terms and arrange in proper order. 5x – 6x = -1x -8y + 3y = -3y Drop the -1, and rewrite. -x – 5y -24x + 15 Explanation -3 -3 -24x + 15 Evaluate the expression: 6(3y − 1) − (5y − 3) 13y – 3 Explanation First, we factor out the values in parentheses. I know this is a bit confusing, however, after we factor out The values in paratheses, we simplify the expressions. It is best to think of it that way instead of adding and subtracting. We will be simplifying like terms and placing the simplified expression in proper order. For example (2x2 + 2x + 2). 6 · 3y = 18y 6 · -1 = -6 The first expression: 18y – 6 Next – (5y – 3) can be rewritten to -1(5y – 3) -1 · 5y = -5y -1 · -3 = 3 Now we have two expressions. 18y – 6 and -5y – 3 18y – 5y = 13y -6 + 3 = -3 Now we have our answer: 13y - 3 Combine like terms: 5x + 7 + 4x – 11. 9x - 4 Explanation 5x + 4x = 9x 7 – 11 = -4 9x – 4 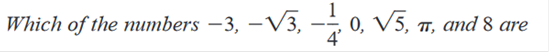
0, 8 Explanation Whole Numbers are 0, 1, 2, 3, 4, 5 à and so on. *No fractions, decimals, irrational numbers, or negative numbers! 
-3, 0, 8 Explanation Integers include all whole numbers and their negative counterpart: <- -4, -3, -2, -1, 0,1, 2, 3, 4 -> Unlike Whole Numbers Integers include negative numbers, but no fractions, irrational numbers, and/or decimals. 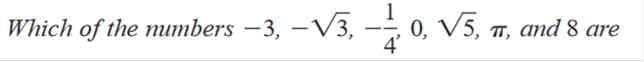
-3, 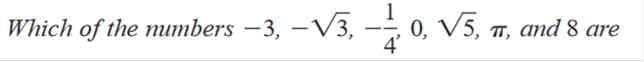
-√3, √5, Evaluate The Expression 6 + 3(-9) -21 Explanation 6 + 3(-9) = 6 + -27 6 + -27 = -21 Evaluate The Expression (-2)2 – 4(-2)(-1) -4 Explanation 4 – 4 · -2 · -1 = -4 Evaluate The Expression -5 + 6 – 12 + 4 -7 Explanation -5 + 6 = 1 1 – 12 = -11 -11 + 5 = -7 Evaluate The Expression 0.05 - 1 -0.95 Explanation -1 – 0.05 = -0.95 Evaluate The Expression (5 – 9) (5 + 9) -56 Explanation 5 · 5 = 25 5 · 9 = 45 -9 · 5 = -45 -9 · 9 = -81 25 + -81 = -56 Evaluate The Expression (878 + 89) + 11 978 Explanation 878 + 89 + 11 = 978 Evaluate The Expression 6 + |3 – 5(2)| 13 Explanation 6 + 10 – 3 = 13 Evaluate The Expression 8 – 3 | 7 – 10 | -1 Explanation 8 -3 | -3 | 8 – 9 = -1 Evaluate The Expression (839 + 974)[3(-4) + 12] 0 Explanation Add 839 and 974 = 1813(3(−4) +12) Multiply 3 · −4 = 1813(−12 + 12) Add −12 and 12 = 1813⋅0 Multiply 1813 · 0 = 0 Evaluate The Expression 974(7) + 974(3) 9,740 Explanation 6818 + 2922 Add 6818 and 2922 9,740 -20 Explanation -.05 x 400 = -20 
Explanation Real numbers are numbers that include both rational and irrational numbers. The Arrow indicates that the number line continues indefinitely (yes, forever). Write the interval notation for the real numbers greater than or equal to 3 and less than 9. [3, 9) Explanation We would use one bracket here because we are not denoting a specific point (on a graph). Write the interval notation of the real numbers greater than 2. (2, ∞) Explanation We would use parenthesis here because Infinity (∞) is not a real number. It indicates a direction. So, when dealing with interval notation and infinity, always enclose ∞ and −∞ with parenthesis. *No Brackets [] in this case. Identify the property that justifies 2(x + 7) = 2x + 14 Distributive Property Explanation Distributive property of multiplication over addition is used when we multiply a value by the sum of two or more numbers. Identify the property that justifies 48 x 1,000 = 1,000 x 48 Commutative Property of Multiplication Explanation Commutative Property of Multiplication means we could change the order of the numbers we are multiplying and it would not change the product. Identify the property that justifies 2 + (6 + x) = (2 + 6) + x Associative Property of Addition Explanation Associative property of addition means that the sum of three or more numbers remains the same regardless of how the numbers are grouped. Identify the property that justifies -348 + 348 = 0 Additive Inverse Property Explanation The additive inverse of a number is its opposite number. If a number is added to its additive inverse, the sum of both the numbers becomes zero. The simple rule is to change the positive number to a negative number and vice versa. Identify the property that justifies 1 x (-6) = -6 Multiplicative Identity Property Explanation Multiplicative Identity property states that any number multiplied by 1 result in the number itself. Identify the property that justifies 0 x 388 = 0 Multiplication Property of 0 Explanation The multiplication property states that the product of any number and zero is zero Use the distributive property to write the sum or difference of: 3x + 30 3(x + 10) Use the distributive property to write the sum or difference of: 7w – 7 7(w – 1) Simplify the expression: 6 + 4x + 2x. 6x + 6 Simplify the expression: 6 + 4(x – 2). 4x – 2 Simplify the expression: 5x – (3 – 2x) 7x - 3 Explanation First factor inside the parentheses. -(3 + 2x) can also be written -1(3 - 2x) -1 x 3 = -2 and -1 x -2x = 2x Next combine like-terms and factor. 2x + 5x – 3 7x – 3 Simplify the expression: x + 10 – 0.1(x + 25) 0.9x + 7.5 Explanation First factor inside the parentheses. – 0.1(x + 25) = -0.1x + -2.5 Next combine like-terms and factor. x -0.1x + 10 + -2.5 also can be written 1x -0.1x + 10 + -2.5 0.9x + 7.5 Simplify the expression: x + 2 Explanation Divide both terms on top by 6. Then put the equation back together in proper order. 6x / 6 = x 12 / 6 = 2 x + 2 Simplify the expression: 4t Explanation Simplify the expression: (-9xy) (-6xy) 54x2y2 Explanation -9 x 54x2y2 Evaluate the expression: b2 – 4ac if (a = -2), (b = 3), and (c = 4). 41 Explanation (-32) – 4(-2)(4) 9 Evaluate the expression: 5 Explanation Evaluate the expression: 3x – 4 when x = 2 2 Explanation 3(2) – 4 = 2 |
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |