Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel

Find the integral.

 

 
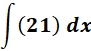
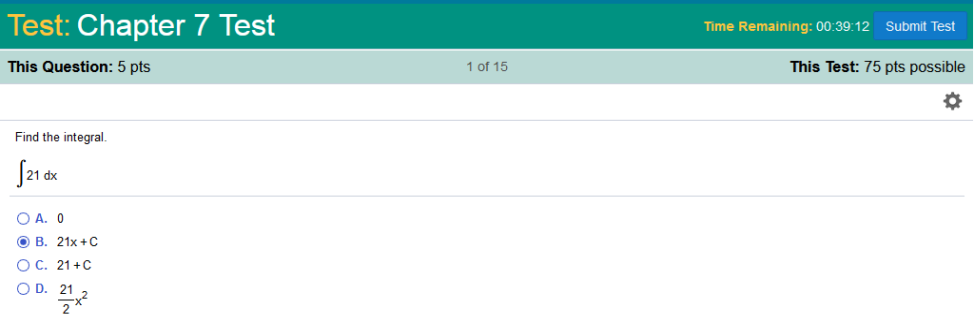
The long way
Apply linearity          
Apply constant rule  
Simplify 21x
Since the constant rule was applied, + C must be added.   Solution = 21x + C
 
https://www.integral-calculator.com/
Enter 21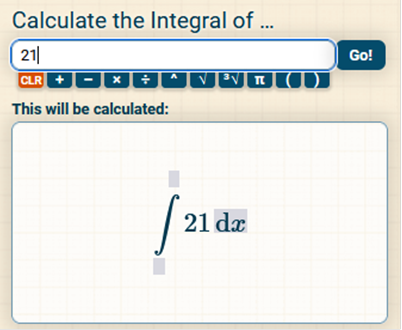

   
Find the integral.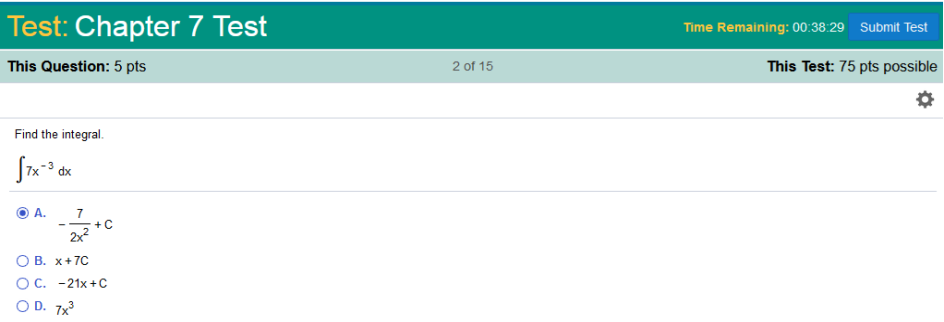
 


 
 
The long way
There are two ways to solve this problem.
We can apply linearity first (convert to a fraction) or we can solve it straight up, using the power rule
and apply linearity when we simplify which is easiest for beginners.
7 is constant with respect to x, so we move 7 out of the integral.
^-3 dx
By the Power Rule, the integral of x⁻³ with respect to x is  x^-2
The reasoning is because the formula for the power rule (integrals) is
 which is the opposite of the power rule for derivatives.
 
So we have )          (x^-3) + C

Now we simplify the right side
)            (x^-3) + C = ) =  x^-2 + C
Now we plug in the 7 which we moved out of the integral
 x^-2 + C =  x^-2 + C
Now we can apply linearity and solve
+ C
 
https://www.integral-calculator.com/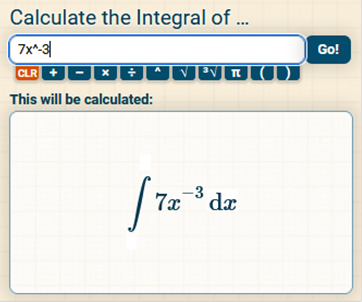
 

   
Find the integral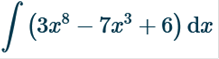
 


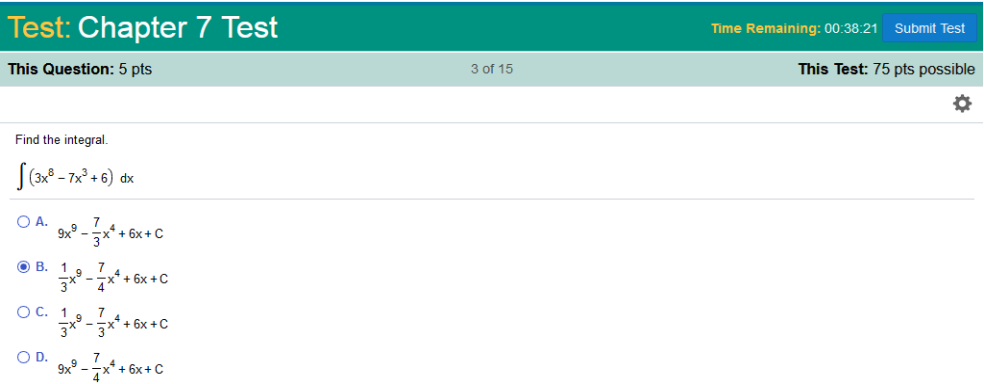
The long way.
⁸ dx – 7 ³ dx + 6  dx
Note: if there is a constant (such as 6), we can move 6 outside the equation and solve for 1.
Then we will multiply the constant by 1 and the solution for the variable.
*The integral of 1 or -1 = (1)x or (1)-x
First, we will solve x⁸ dx with the power rule.        =        
we can place the 3 on top  or    
 
next, we will solve x³ dx with the power rule.        =        
we can place the -7 on top               
 
next, we will solve 1 dx with the power rule.         =   
 
we can multiply 6(1)x =                      6x
we can move all negatives and x values to the right of the fractions
 
x⁹ – x⁴ + 6x + C
 
 
https://www.integral-calculator.com/
Enter the equation exactly like below.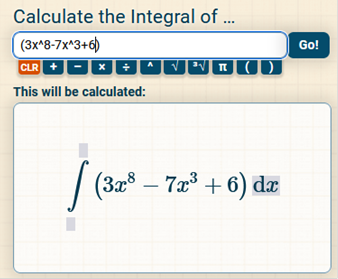

 

Find the integral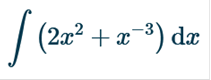
 




² + ^-3) dx

2 is a constant, so we can move it in front of the equation
² + ^-3 dx
.
n = the exponent.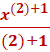
            =  =

So, we have + ^-3 dx

Integrals of negative exponents are a little tricky.
                

we will move the negative from -2 beside the fraction and finalize the answer.
 +  + C

https://www.integral-calculator.com/
Enter the equation exactly like below.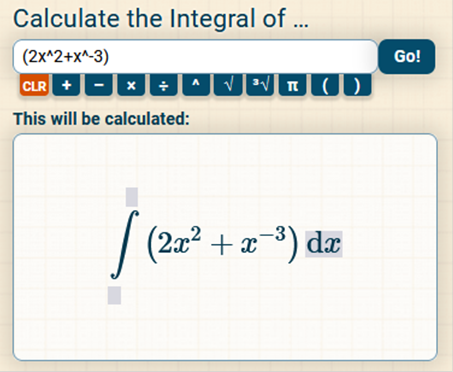
 
 
   
Find the integral
 


 
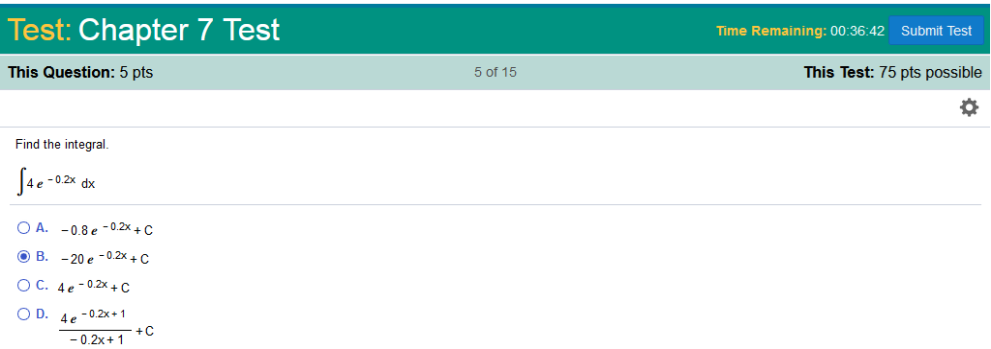
There is a long way to do this problem, however, all we need to do here is
divide 4 by 0.2 and replace 4 with 20.
^-0.2x dx
4 / 0.2 = 20
The integral of ^-0.2x dx =             ^-0.2x dx
The same steps will work with ^-0.2x dx as well.
3 / 0.2 = 15
The integral of ^-0.2x dx =             ^-0.2x dx + C
   
Find the integral
 


 
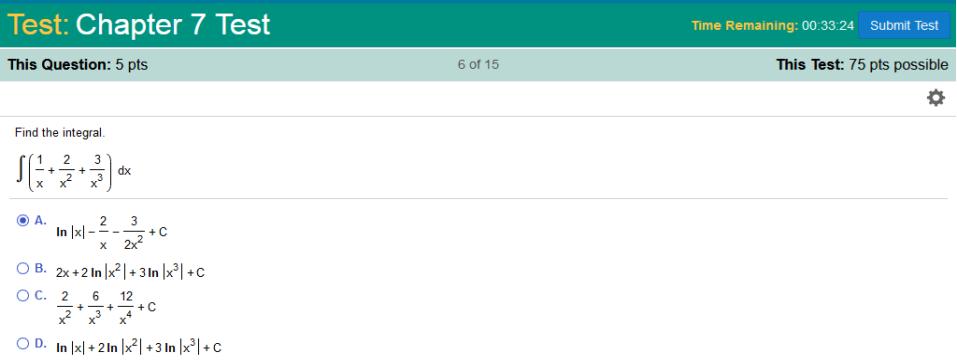
The long way.
The integral of   =            ln|x|  (this is standard)
So, we have             ln|x| +
Next, we will solve
Since 2 is constant with respect to x, move 2 out of the integral, and we will move x² to the numerator and it will be negative.
Solve                 ^-2        2     2        
we can move x^-1 down (it will be positive) and rewrite   then eliminate unnecessary numbers

 
Solve                    3 ^-3              3      
We can move x^-2 down (it will be positive) and rewrite   (move the negative to the left side)
Answer:     ln|x| -  -
 
https://www.integral-calculator.com/
Enter the equation exactly like below.

   
Find C(x) if C’(x) = √x and C (9) = 40
 

 
First, we need to find the integral of: √x
https://www.integral-calculator.com/ Enter (sqrt(x))
 

Now we plug in the value of 9 for x, add x, and solve for x like so.
 + x = 40
Plug in values                     2(9)^3/2 ÷ 3 + x = 40
Simplify                                18 + x = 40
Subtract 18                          x = 22
Since C’(x) = √x we must use the integral, add the value of C(x),
and rewrite the equation like below.
C(X) =  + 22  
Find the integral.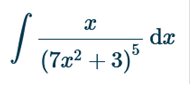
 

 

 

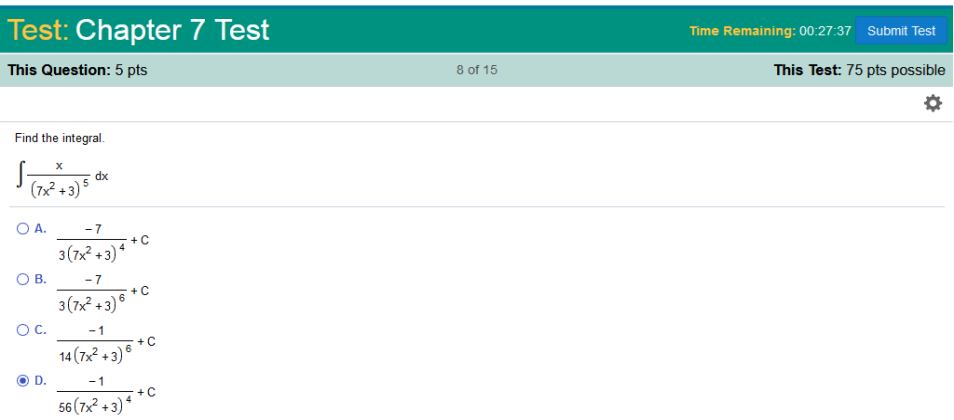
First, we need  [7x² + 3] which = 14x <- (this is the derivative of 7x² + 3)
 
We now have (14x)⁵ so we will Rewrite the problem using u and du        (in this case u = 7x² + 3)
 
This will be  then we will combine             
 
Since  is constant with respect to u, move  out of the integral.           du
 
Next, we will move u5 to the numerator by raising it to the -1 power and end up with  u^-5 du + C
Next, we need to work on u^-5 du this =   ^-4  =  rewrite ^-4
So, we have ^-4 + C
 
Lastly, we simplify and replace all occurrences of u with (remember u = 7x² + 3)
 
u^-4 = -u^-4 replace u with 7x² + 3
 
       (note: by moving the exponent -4 down, it will become positive)
 
https://www.integral-calculator.com/
Enter the equation exactly like below.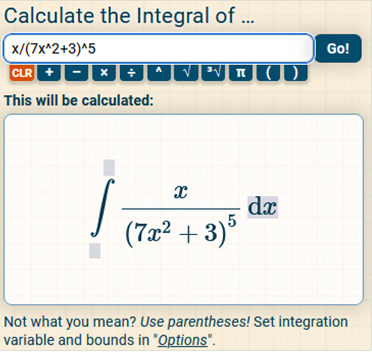
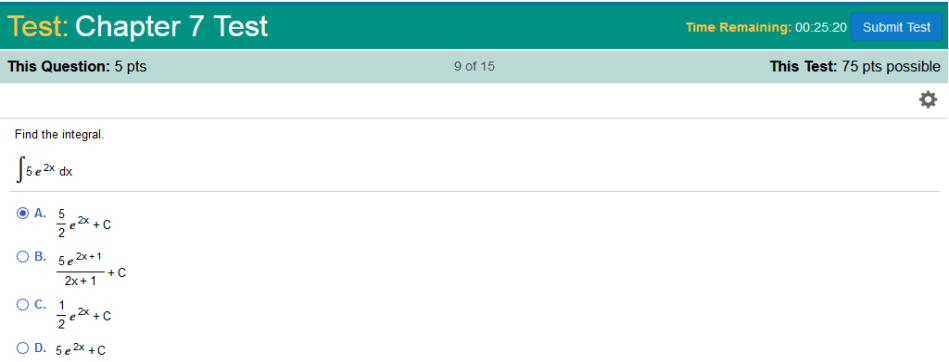
Find the integral.


 
Simply divide the constant, 5, by 2 , and replace the fraction for 5.
 
 e^2x + C
 
This would be true with
also, except, we could simplify
             would =            or  
No worries!
https://www.integral-calculator.com/
Enter the equation exactly like below.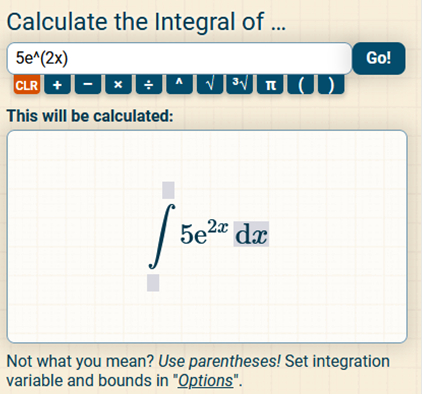

   
Approximate the area under the graph of​ f(x) and above the​ x-axis using n rectangles.
f(x) = 2x³ – 1 from x = 1 to x = 6; n = 5; use right endpoints.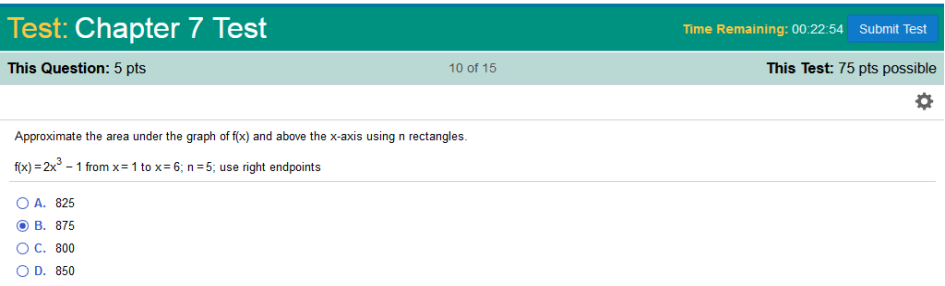
 

 
We will use 2x³ -1 to solve this problem.  Lower limit 1, upper limit 6, n = 5
So, we will add 1 + 6, and subtract 5
6 + 1 – 5 = 2
 
We will start at f(2) through f(6)
 
f(2) = 2x³ -1 =     2(2)³ -1 =              15
f(3) = 2x³ -1 =     2(3)³ -1 =               53
f(4) = 2x³ -1 =     2(4)³ -1 =              127
f(5) = 2x³ -1 =     2(5)³ -1 =              249
f(6) = 2x³ -1 =     2(6)³ -1 =              431
 
15 + 53 + 127 + 249 + 431 =         875
 
https://www.emathhelp.net/calculators/calculus-2/riemann-sum-calculator/
enter equation and values,
find right end points.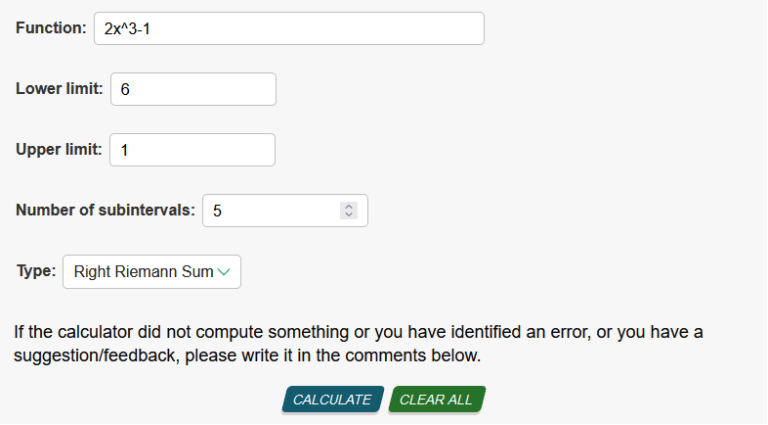
`
   
Evaluate the definite integral.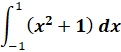
 

 

 
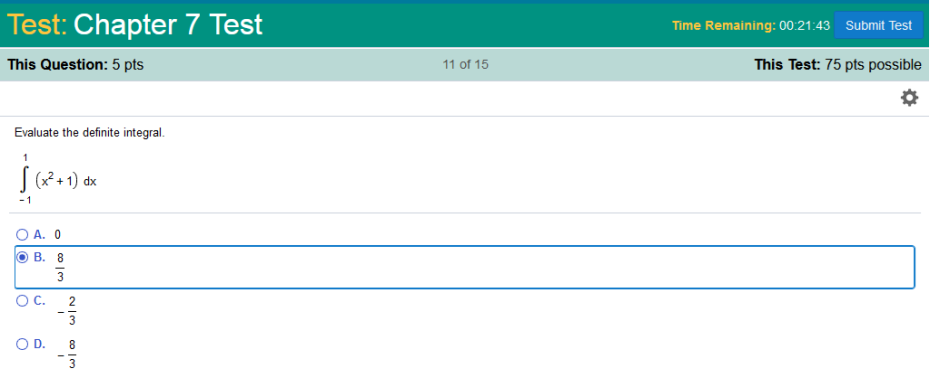
First, we Split the single integral into multiple integrals.
 

    =  we can move x³ over       ³
 
so, the integral of 1 = x
 
We have      ³ so we need to plug in 1 and -1, and simplify
 
(³³ =                   +  =       
 
https://www.integral-calculator.com/
Enter the equation exactly like below.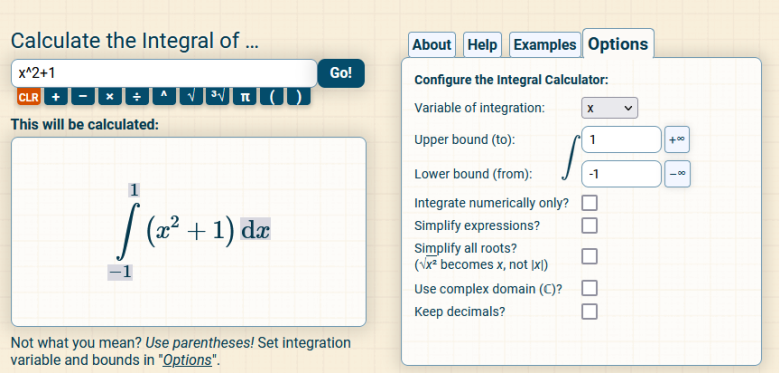
 
Evaluate the integral.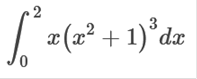


 
The easiest way to do this is to simplify x(x² + 1)³
You should have some type of calculator that will do this for you. However, the easiest way to simplify is like so
first (x² + 1)³

x²⁽³⁾ + 3x²⁽²⁾ · 1 + 3x² · 1² + 1³

x⁶    + 3x⁴     · 1 + 3x² · 1² + 1³

x⁶ + 3x⁴ + 3x² + 1
now we have x (x⁶ + 3x⁴ + 3x² + 1) =                x⁷ + 3x⁵ + 3x³ + x

Now we need to find the integral of                                      x⁷ + 3x⁵ + 3x³ + x
We can do these one by one which makes it simple.
We can do the first and simply follow the pattern.
x⁷ can be written as   1x⁷ so we move 1 outside the integral (it is constant), remember?
x⁷        =        now we move the 1 up and move x⁸ over!
 
The integral x⁷      =                      x⁷
We do not need to do the rest, because they are similar done the same way
x⁶            =          x⁷
+ 3x⁴         =          x⁵
+ 3x²         =          x⁴
+ 1 x          =          x²

So, we need to plug in the upper and lower limits, and subtract
x⁷x⁵ x⁴ x²) - x⁷x⁵ x⁴ x²)

Upper limit = 2, lower limit = 0
(2)⁷(2)⁵ (2)⁴ (2)² ) – ((0)⁷(0)⁵ (0)⁴ (0)² =            78
 
https://www.integral-calculator.com/
Enter the equation exactly like below.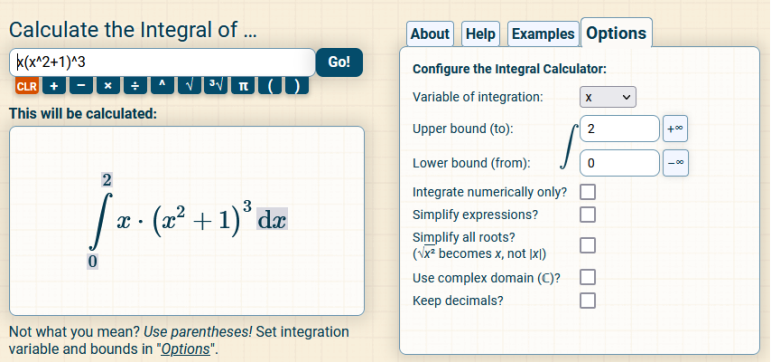

Use the definite integral to find the area between the​ x-axis and​ f(x) over the indicated interval.
f(x) = 2x + 7, (1, 5)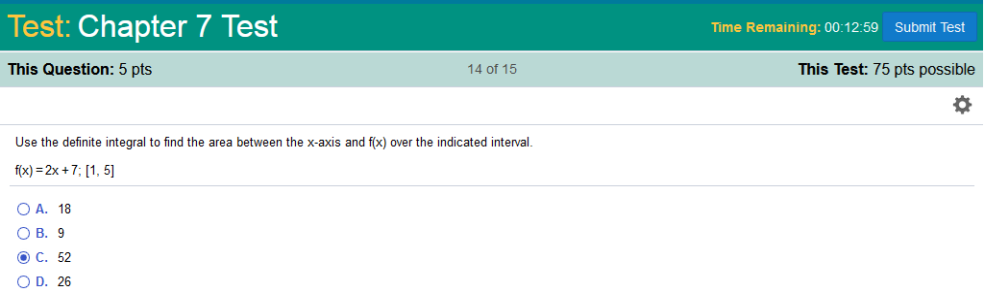


f(x) = 2x + 7, (1, 5)       =         
 
+                  = x²
 
+        
 
So, we have    x² + 7x and now we plug in the upper and lower limits and subtract
 
         5                 1
(x² + 7x) – (x² + 7x)                  ((5)² + 7(5)) – ((1)² + 7(1))
                                                             60      -          8         = 52                                                                       
https://www.integral-calculator.com/
Enter the equation exactly like below.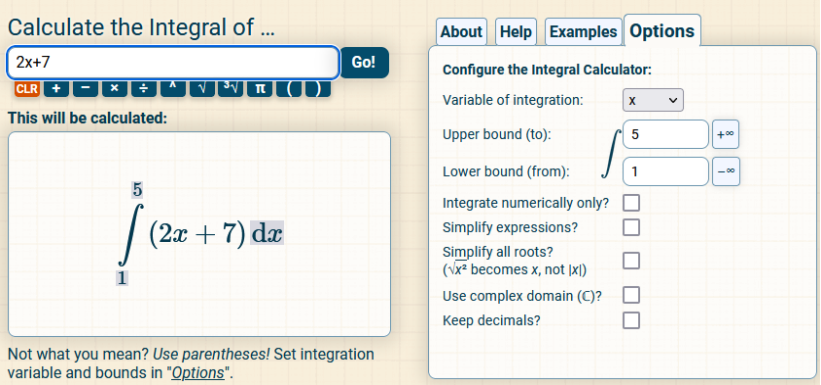
 

  A company has found that its rate of expenditure​ (in hundreds of​ dollars) on a certain type of job is given by
E’(x) = 6x + 4 where x is the number of days since the start of the job.
Find the total expenditure if the job takes 3 days.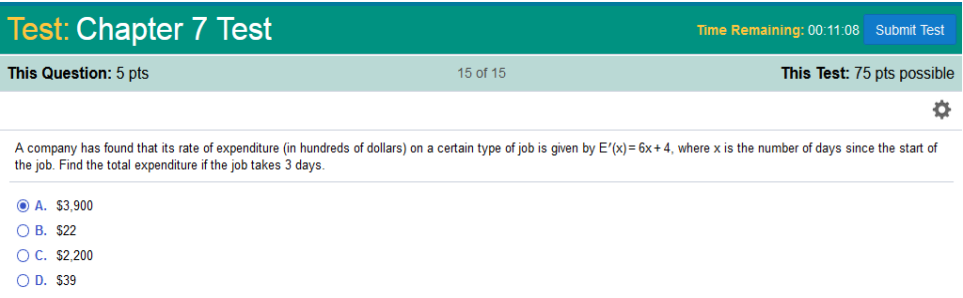

We have the equation E’(x) = 6x + 4 and since we are looking the total expenditure for 3 days,
the lower limit starts at 0, and the upper limit ends at 3. This will be in hundreds of dollars.
That means we will multiply the solution by 100…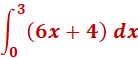
 

 
 (We have already done this several times. We simply add 1 to the exponent x^{1 + 1} and divide 6 by 1 + 1) =    3x²
     (We have already done this several times. The integral of a constant is the constant times x)            =          4x
 
So, we have 3x² + 4x
Now we plug the lower and upper limits in and subtract.

         3                    0
(3x² + 4x) - (3x² + 4x)
 
(3(3)² + 4(3)) - (3(0)² + 4(0))
          39            -             0                = 39
 
39 in hundreds, so it is 39 ·100 = $3,900
 
https://www.integral-calculator.com/
Enter the equation exactly like below.
 

 

---

---