Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel

Find the minimum absolute extremum as well as all values of x where it occurs on the specified domain.
    f(x) = x³ - 3x²; [0, 4]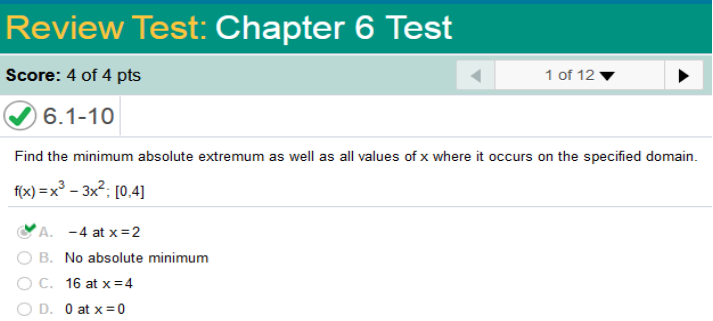
 

 
The long way
Find the derivative, then solve for x and zero (0).
(2)²-3(2)
f(x) = x³ - 3x²– derivative =                                       3x² – 6x = 0
Next, we factor the left side of the equation.
3x (x – 2) = 0
Now we can factor each expression!
3x = 0              divide both sides by 3 (0 / 3 = 0)                   x = 0
x – 2 = 0           add 2 to both sides 0 + 2 = 2)                         x = 2
 
if we plug 0 into the equation, it will equal 0, so we will plug in 2 into f(x) = x³ - 3x²
f(x) = (2)³ – 3(2)² =             -4        the answer is             -4 at 2
 
To solve this problem, we need to find the Local Minima and the Local Maxima
This calculator will find and compare those to the graphs.
https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/
 


  Find the minimum absolute extremum as well as all values of x where it occurs on the specified domain.
x³ – 2x² + 3x – 4; [-2, 5]
 

Find the derivative, then set equal to 0 and solve for x.
 
The derivative of x³ – 2x² + 3x – 4 =             x² – 4x + 3=0
 
We need to factor: x² − 4x + 3 = 0
(x – 1) (x - 3) = 0
x – 1 = 0 =     1
x – 3 = 0 =     3
Now we plug 1 into the original equation: x³ – 2x² + 3x – 4
(1)³ – 2(1)² + 3(1) – 4 =      
THE ANSWER =
 
https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/

   
Find the maximum absolute extremum as well as all values of x where it occurs on the specified domain.
f (x) = 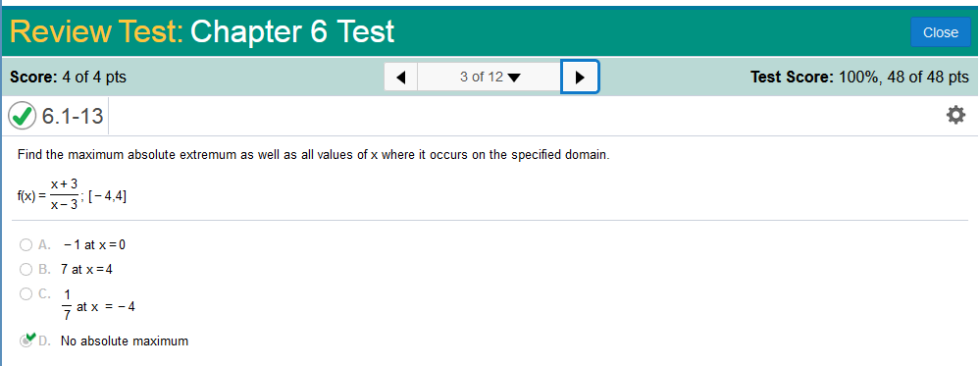; [-4, 4]
 

 
The long way
Find the derivative of f (x) =  set value to 0, and solve for x.

 
f = x + 3
g = x – 3
f’ = x
g’ = x
 =  =
 = 0
 
No Solution
To solve this problem, we need to find the Local Minima and the Local Maxima
https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/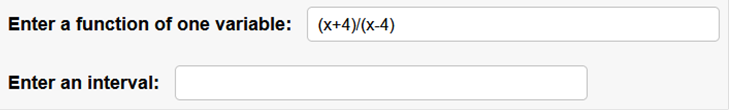
P(x) = -x³ + 12x² -36x + 400, x ≥ 3 is an approximation to the total profit​ (in thousands of​ dollars)
from the sale of x hundred thousand tires. Find the number of hundred, thousands of tires that
must be sold to maximize profit.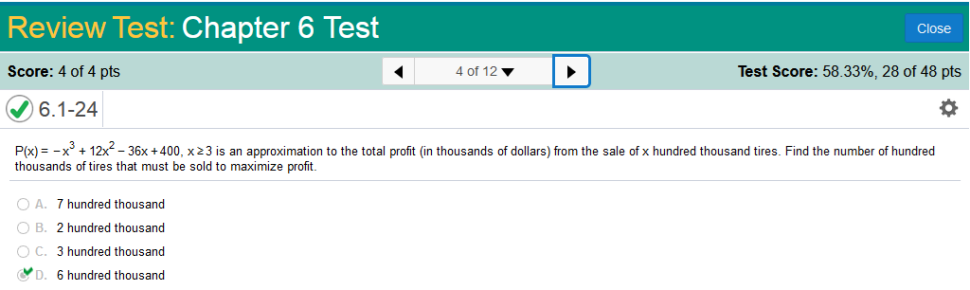

Find the derivative of -x³ + 12x² -36x + 400, set value to 0, and then solve for x.
Derivative of -x³ + 12x² -36x + 400 =  -3x² + 24x - 36
Set value equal to 0.     -3x² + 24x - 36 = 0        solve for x.
x = 2 or 6
we need to factor -3x² + 24x - 36 = 0 which is −3 (x−6) (x−2)
Simplify     −3 (x−6) (x−2) = 0
x – 6 = 0
x – 2 = 0
Calculate: x – 6 = 0, add 6 to both sides         x = 6
Calculate: x – 2 = 0, add 2 to both sides         x = 2
x = 6, 2
6 (thousand) must be the answer because 6 (thousand) would be the greater number.
   
Find the dimensions that produce the maximum floor area for a​ one-story house,
 that is rectangular in shape and has a perimeter of 166 ft.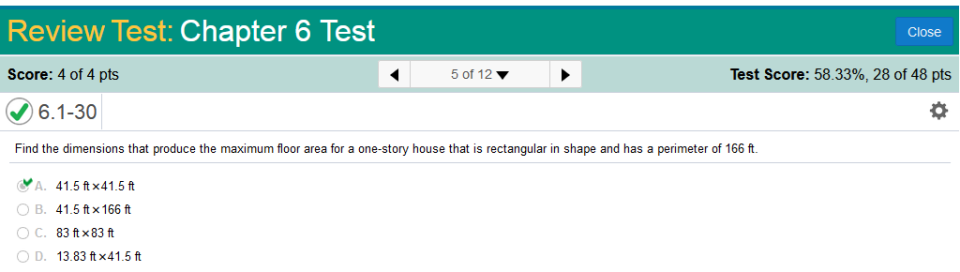
 

 
We have already worked on this type of problem. It is the perimeter of a rectangle,
So, once we have two sides, all we need to do is divide by 2, and subtract our results…
to find the other half of the solution.
We simply divide the perimeter by 2, subtract 2x, set at zero (0), and solve for x.
 
  – 2x = 0            Answer = 41.5
 
Steps:
Simplify the fraction: divide 166 by 2 = 83
83 - 2x = 0
Simplify: subtract 83 from both sides.
-2x = -83
Simplify: divide -2 by both sides.
x = 41.5
 
Solve for the other half of the rectangle.
166 – 83 = 83
83 ÷ 2 = 41.5
41.5 – 41.5 = 0
 
Find the dimensions that produce the maximum floor area for a​ one-story house that is rectangular
in shape and has a perimeter of 168 ft.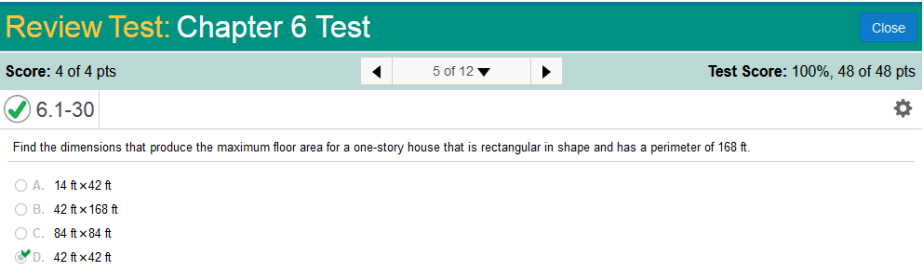
 

I solved this problem by first writing this formula and solving for x
168 ÷2 – 2x = 0                       84 – 2x = 0
Subtract 84 from both sides.
84 – 84 -2x = 0 + 84                 -2x = 84
Divide both sides by 2.           x = 42
Since two sides are equal at 42 and the perimeter is equal to 168, we can write this equation.
2(42) + 2x = 168          84 + 2x = 168
Subtract 84 from both sides.             2x = 84
Divide both sides by 2.                       x = 42
The answer is 42 ft. x 42 ft. An architect needs to design a rectangular room with an area of 68 ft² squared.
What dimensions should he use in order to minimize the​ perimeter?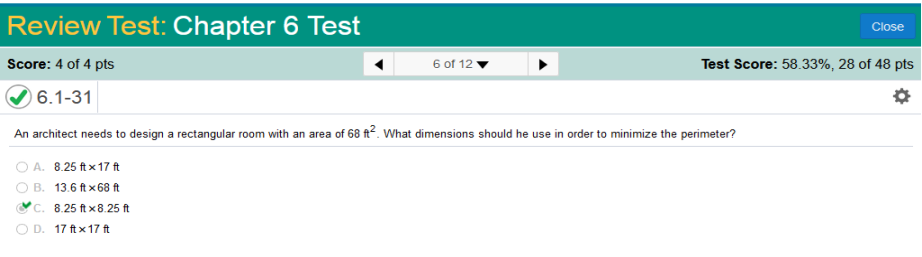
 

I have done quite a few of these, and the simple way solution is the √68,
Which is 8.246211251 (8.25 x 8.25)
However, we will do this the long way.
 
2(68/x) + 2x         136/x + 2x
-136/x² + 2 = 0
-136/x² = 2
x² = 68
x = √68
x = 8.246211251
Round up to 8.25 ft.
  An architect needs to design a rectangular room with an area of 76 ft² squared.
What dimensions should he use in order to minimize the​ perimeter?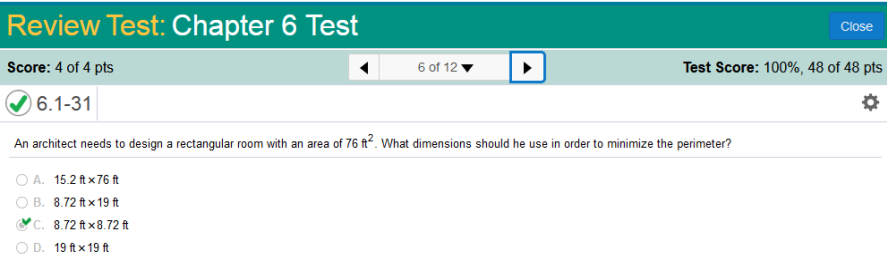
 

 
2(76/x) + 2x
152/x + 2x
-152/x² + 2 = 0
-152/x² = 2
x² = 76
x = √76
x = 8.717797887
Round up to 8.72 ft.  
If the price charged for a candy bars is​ p(x) cents, then x thousand candy bars will be sold in a certain​ city,
where p(x) = 7 –

How many candy bars must be sold to maximize​ revenue?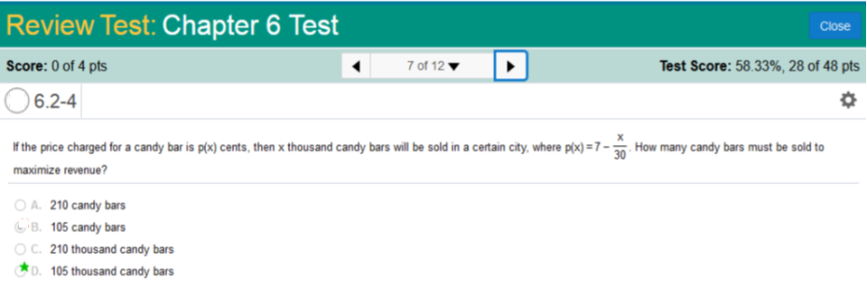
 

 
Rewrite the equation that we need to solve.
This is the equation that we need to solve.
30 -  = 0 and solve for x.
 
Steps to solve.
Subtract 30 from both sides of the equation:  = −30
Multiply both sides of the equation by  :
 ()           (-30)
 
-30 · -7 ÷ 2         210 ÷ 2 = 105         x = 105
If the price charged for a candy bars is​ p(x) cents, then x thousand candy bars will be sold in a certain​ city,
where p(x) = 84 –

How many candy bars must be sold to maximize​ revenue?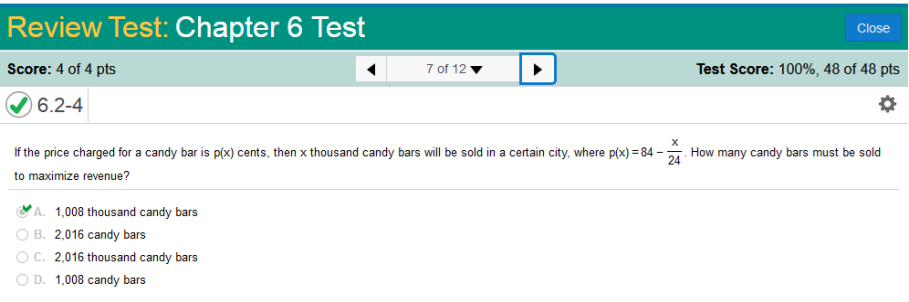


Solve for x and zero 84 – 2x / 24 = 0, x = 1,008 in thousands
 
This is similar to what we have been working on.
We simply use the formula we are given however we place a “2”
in front of x, set to zero (0), and solve for x.
Like so…
 = 0
 
Solution is 1,008
You can use online calculators to solve these calculate some of these,
However, I always liked to solve them myself because practice makes perfect.
 = 0

Simplify the fraction by dividing the top and bottom by 2.
 = 0

Simplify: Subtract 84 from both sides of the equation.
 = -84

Simplify: Multiply both sides of the equation by −12.
x = -12 · -84
x = 1,008  
A rectangular field is to be enclosed on four sides with a fence. Fencing costs $5 per foot for two opposite​ sides,
and $3 per foot for the other two sides. Find the dimensions of the field of area 870 ft² that would be the
cheapest to enclose.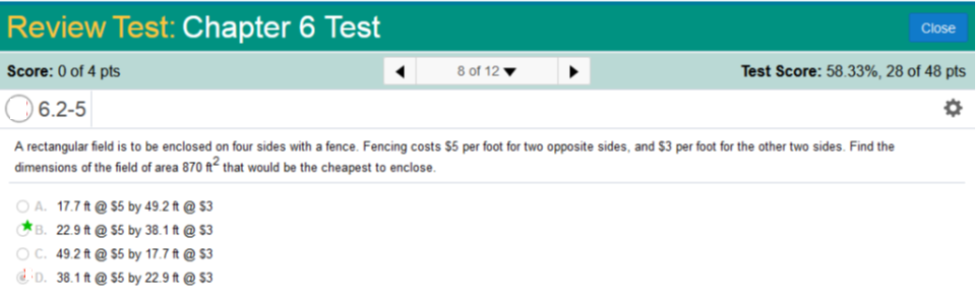
 

2(5) + 2x(3) ()
Combine values.                    10 + 6x()
Combine values again.          10 -
Set to zero                              10x -  = 0
 
Solution: 22.84731931 or -22.84731931
Since we the value to be positive for the final part of the problem,
I will show the steps to solve for 22.84731931
10x -  = 0
 
Subtract 10 from both sides of the equation.
 = -10
 
Simplify to eliminate the fraction. (Multiply both sides by x²)       5220 = 10x²
Simplify: divide both sides by 10.                                                     522 = x²
Simplify by specifying the square root of both sides.                      x =
The square root of 522 = 22.84731931 (do not round yet)
To solve the second part of this problem, we need to divide 870 by our first solution.
870 / 22.84731931 =              38.07886553
Now we can round both values.                   22.9 ft @ $5 by 38.1 ft @ $3
----------------------------------------------------------------------------------------------------------------------------------------------------
Find the elasticity of demand E for the demand function q equals 7,300 - 17p.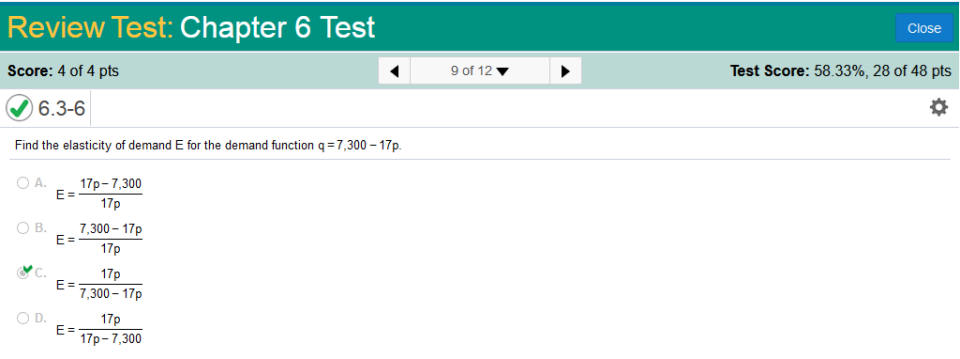

E =  
 
Let’s find q (not to be confused with dq)
q used in this case is the derivative of the given q (7,300 - 17p)
So, q = -17 or  because it is the derivative of 7,300 - 17p
and needs to be multiplied by a fraction.
That is all the calculus for this problem.
The rest is simply multiplying the fractions.
Next, we simply multiply p over dp or
 
   =
 
Given the demand function q = 293 - 3p, calculate the elasticity of demand when p = 57.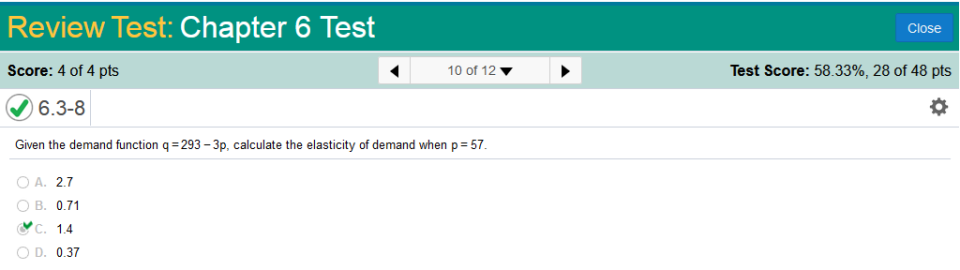
 

 
P = 57, so I wrote this in one equation, otherwise, you would need to calculate multiple equations.
It is as simple as this. Watch the way I set up the values.
And you can enter it in your calculator exactly as I wrote it (no spaces).
 
3 · 57 / (293 – 3 · 57)
 
1.401639344
Round to 1.4
----------------------------------------------------------------------------------------------------------------------------------------------------
The demand for boneless chicken​ breast, in dollars per​ pound, is given by q = -0.6p + 4, where p
represents the price per pound and q represents the average number of pounds purchased per week,
per customer. Determine the price at which the demand for boneless chicken breast is unit elastic.
 

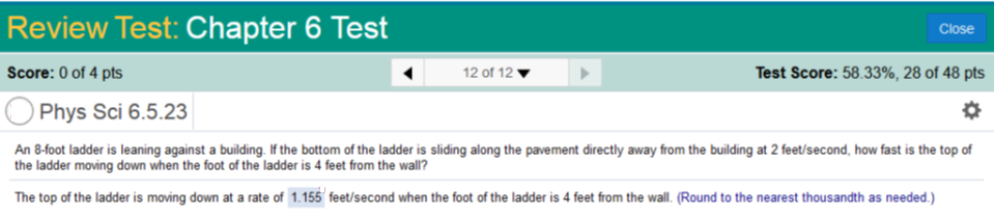
I have seen this problem (with different values) on other websites and most, if not all,
had long and confusing formulas to solve it, and most had failed miserably.
Look closely at how I set up the values. This is the simplest way to solve this problem.
I have tested it on the same problems and got the right answer every time!
(-0.6)  = 1

It is best to do this the long way because most calculators will not simplify the proper way.
We need to divide three values by 0.2 and rewrite the equation to simplify.
I have color coded the values, so it is easy to follow.
 
-0.6 ÷ 0.2 = -3
0.6p ÷ 0.2 = 3p
-4 ÷ 0.2 = 20
Now we will put the values back together.
-3 · = 1
We will simplify ever further by multiplying (  by )
- = 1

Now we will simplify the left side by multiplying: 3p – 20 times 1.
-3p = 3p – 20
Now we will subtract 3p from both sides.
(-3p + -3p) = (3p – 3p) – 20
-6p = -20
Now we will divide -20 by -6 = 3.333333333
Round to the nearest penny.
$3.33 per pound

---

An 8-foot ladder is leaning against a building.
If the bottom of the ladder is sliding along the pavement directly away from the building at 2 feet/second,
how fast is the top of the ladder moving down when the foot of the ladder is 4 feet from the​ wall? 

This is the equation I wrote to solve this one!
You need to do it in the correct order, or the answer will be different.
Any scientific calculator will solve it this way.
Solve this first            4 ÷ ( = .5773502692

Then multiply by 2.    .5773502692 · 2 = 1.154700538

(Round to the nearest thousandth)        1.155
It will not really work out if you enter the entire equation.
You need to follow the exact order!

---

---