|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Calculus For Business
Test 5 f(x) = 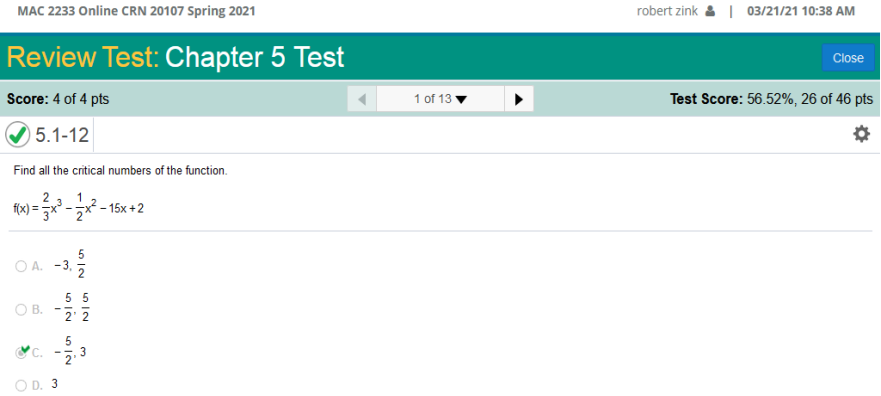
Use the first numbers in (x,f(x)). To find the critical numbers of a function the long way we must find the derivative, set the derivative to equal zero (0), and solve for x. First find the derivative of: f(x) = 3( 2(- 1(-15x1-1) = 15 2 ( - 1) = 0 Derivative is: 2x2 – x – 15 Then set the derivative to equal zero (0). 2x2 – x – 15 = 0 Solve quadratic equation http://coursesavior.com/free/quadratic-equation-solver/ 3, -2.5 (or -5/2) This calculator will find the critical points. Enter in precisely as shown and scroll down to Critical Points https://www.emathhelp.net/calculators/calculus-1/function-calculator 
Find all the critical numbers of the function. f(x) = 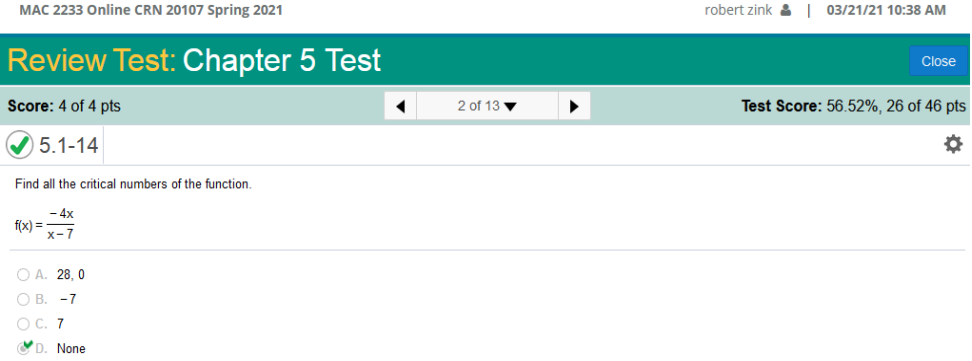
To find the critical numbers of a function the long way we must find the derivative, set the derivative to equal zero (0), and solve for x. The derivative = 0, therefore there are no Critical Points. Let’s simplify the equation to see for ourselves! f(x) = To simplify we would do so by: x – (x) = 0 -4 – (7) = -11 The derivative of -11 = 0 therefore there are no critical points! This calculator will find the critical points. Enter in precisely as shown and scroll down to Critical Points https://www.emathhelp.net/calculators/calculus-1/function-calculator 
Scroll Down to Critical Points No critical points. https://www.derivative-calculator.net/ 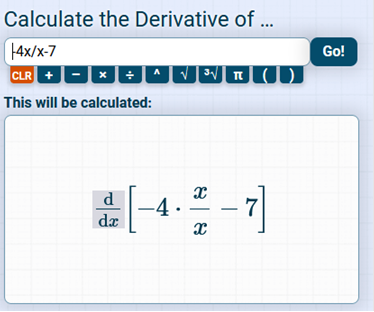
y = x4 – 18x2 + 81 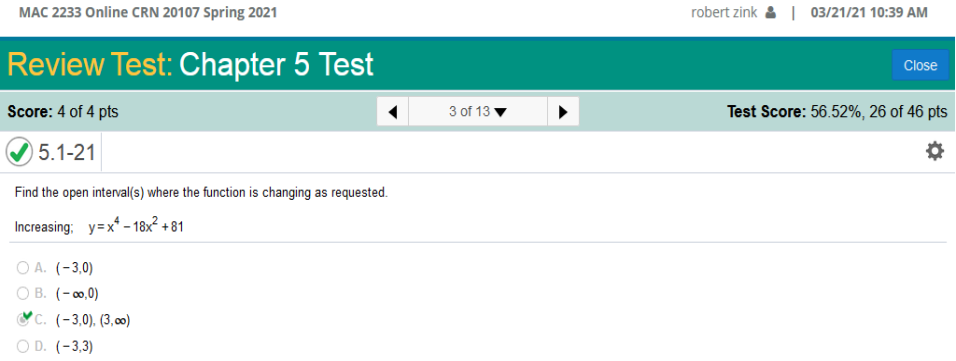
The long way. To find the Intervals of Increase of this function the long way we must find the derivative, set the derivative as so, and solve for x. Let’s find the derivative of x4 – 18x2 + 81. nn –1 4(x4 – 1) = 4x3 2(-182 – 1) = -36x 81(0) = 0 Derivative = 4x3 – 36x Then we set up the equation. Since we are looking for the intervals of increase, we must use the greater than sign (>) and set at zero (0) 4x3 – 36x > 0 factored = 4x (x2 – 9) = 0 Then we must factor some more and set each set to equal zero (0) 4x(x2 – 32) = 0 4x(x + 3)(x – 3) = 0 So, we have 4x(x + 3)(x – 3) = 0 What we can do next is set each to equal zero. 4x = 0 x + 3 = 0 x – 3 = 0 4x = 0 = 0 x + 3 = 0 = -3 x – 3 = 0 = 3 the answer = (-3,0) U (3,∞) https://www.emathhelp.net/calculators/calculus-1/function-calculator Intervals of Increase 
Scroll Down to: 
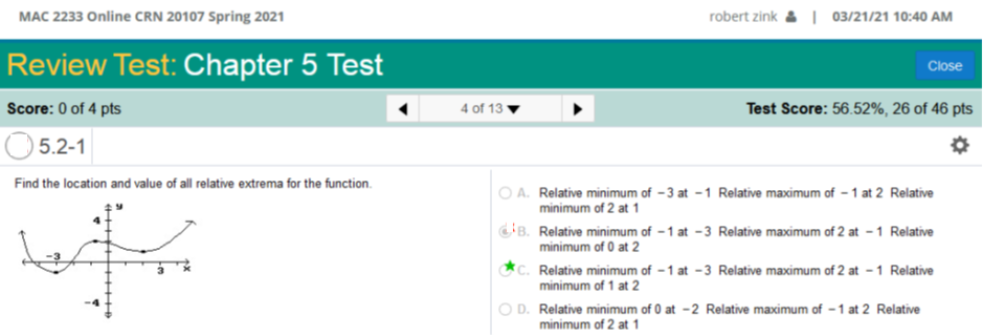
Explanation! A function has relative minimum at x = a, if f'(a) = 0 and f" (a) > 0 (concave upward) and Relative maximum at x = b, if f'(b) = 0 and f" (b) <0 (concave downward). 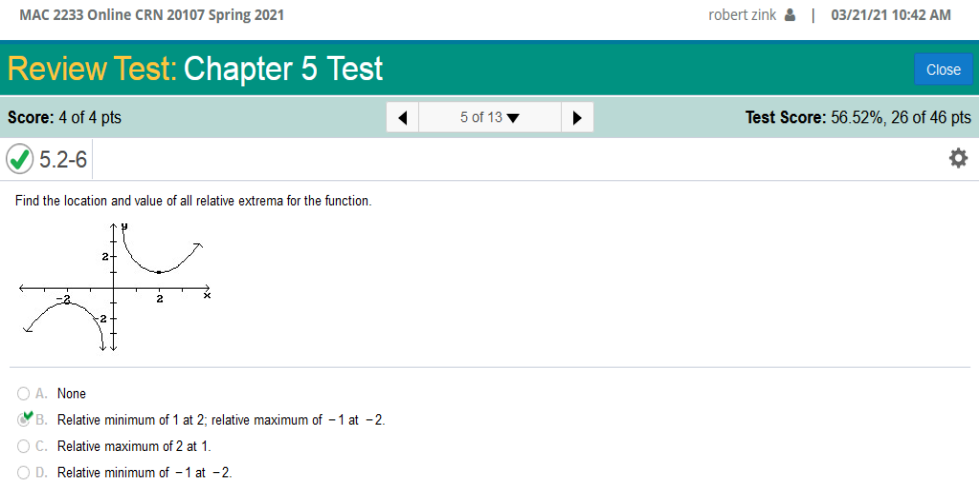
Explanation! A function has relative minimum at x = a, if f'(a) = 0 and f" (a) > 0 (concave upward) and Relative maximum at x = b, if f'(b) = 0 and f" (b) <0 (concave downward). R(x) = 500x - .03x2 and C(x) = 160x + 100,000 where x denotes the number of clocks made. What is the maximum annual profit? 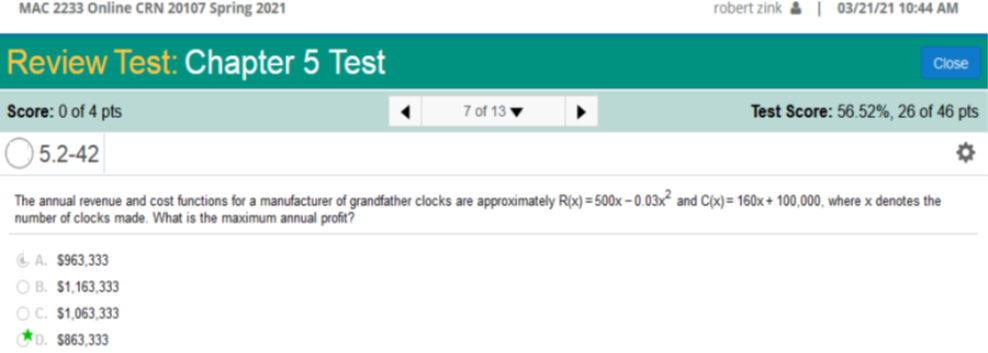
This is a little tricky, but we solve it like so… Values: R(x) = 500x - .03x2 and C(x) = 160x + 100,000 Gather values: 500x - .03x2 – 160x – 100,000. Simplify: 500x - .03x2 – 160x – 100,000 = 340x - .03x2 – 100,000 Find derivative 340x - .03x2 – 100,000 = 340 - .06x (*We need to plug in final value into this derivative) Solve for x 340 - .06x = 5666.67 plug in to equation 340(5666.67) - .03(5666.67)2 – 100000 = 863,333 Find the number of units, x, that produces the maximum profit P, if C(x) = 40 + 52x and p = 84 – 2x. 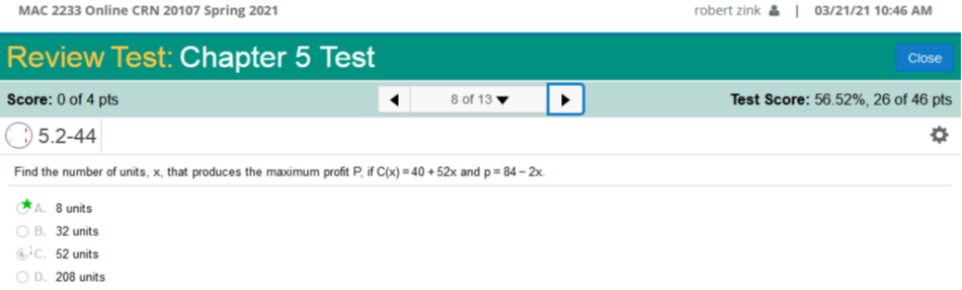
First set up the equation x (84 – 2x) – 40 – 52x Simplify -2x2+ (84x – 52x) – 40 simplify -2x2 + 32x – 40 Find the derivative of -2x2 + 32x – 40. 2(2x2 – 1) = -4x 1(32x1 – 1) = 32 -40(0) = 0 Derivative = -4x + 32 Now set the equation to 0 and solve for x. -4x + 32 = 0 Add 4x to both sides. 32 = 4x Divide both sides by 4. x = 8 f(x) = x2 + 2x + 1 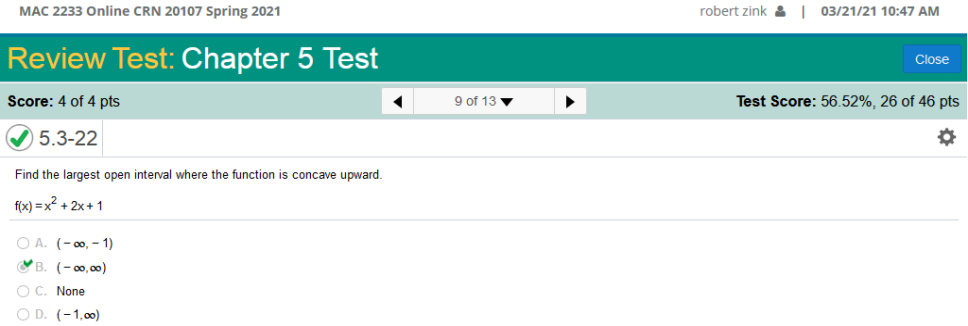
To solve this problem, we need to find the Domain, however there is no Domain, So, we use Interval Notation: (−∞, ∞). Use the functions calculator. https://www.emathhelp.net/calculators/calculus-1/function-calculator 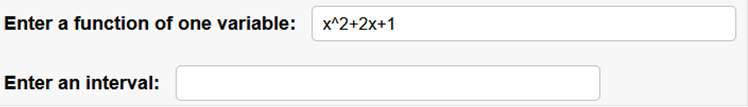
Scroll down to  
The reason there is no Domain, and determined Interval Notation is because there is no Real Number to make the expression undefined. Decide if the given value of x is a critical number for f, and if so, decide whether the point is a relative minimum, relative maximum, or neither. f(x) = x5; x = 0 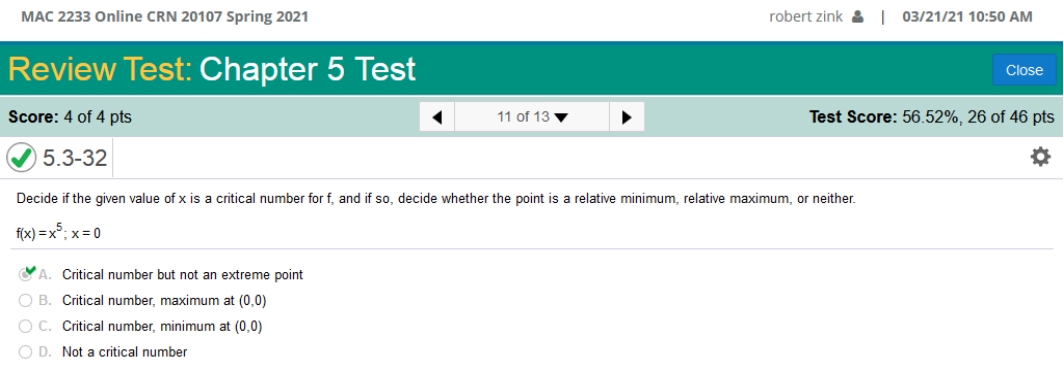
To solve this problem, we can use the first or second derivatives or not. We can set both equations to zero, solve for x, and the critical number will be 0. However, there is no extreme point because there are no ordered pairs. x5 = 0 1ST Derivative: 5x4 = 0 = 0 2ND Derivative: 20x3 = 0 = 0 Graph the function, considering the domain, critical points, symmetry, regions where the function is increasing or decreasing, inflection points, regions where the function is concave upward or concave downward, intercepts where possible, and asymptotes where applicable. f(x) = -6x3 – 36x2 + 216x - 11 
Explanation 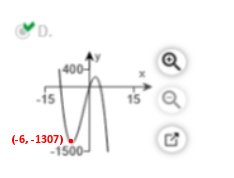
It takes a little practice, but you can look at all the other graphs, and see the above is the correct graph. To solve this problem, we need to find the Local Minima This calculator will find and compare those to the graphs. https://www.derivative-calculator.net/ In this case, Local Minima are (-6, -1307) You can find the Local Minima below. Enter the equation as shown below. Solve this problem the long way. Find the first derivative, set at zero, and solve for x. I won’t put all the steps to finding the derivatives because you should know how to do that by now. Or use this calculator. https://www.derivative-calculator.net/ Find the derivative of: -6x3 – 36x2 + 216x – 11. First Derivative -18x2 – 72x + 216 Set to equal 0 and solve for x. -18x2 – 72x + 216 = 0 We need to factor -18x2 – 72x + 216 This is from Algebra 1, so I will not show the steps. -18x2 – 72x + 216 factored out = -18(x – 2) (x + 6) Next, we do what we did above -18 = 0 = 0 x – 2 = 0 = 2 x + 6 = 0 = -6 The first local minima we need would be (-6) To find the second local maxima we need to find the “y value” when x = -6 This is true because the value of the second derivative is positive. All this means is we plug in the value -6 to the ENTIRE equation, which means f(x). *Just a note, you would not need to go any further, because none of the other graphs represented a “local maximum” of “-6”, however, we will solve it anyway. f (x) = -6x3 – 36x2 + 216x – 11 f (-6) = -6(-6)3 – 36(-6)2 + 216(-6) – 11 f (−6) = 1296 – 1296 – 1296 – 11 f (−6) = −1307 (We do not need to divide by -6 in this case, because we do not need f to stand alone) Local Maxima = (-6, -1307) Now we can compare the graphs and get the answer right! https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/ 

Graph the function, considering the domain, critical points, symmetry, regions where the function is increasing, or decreasing, inflection points, regions where the function is concave upward or concave downward, intercepts where possible, and asymptotes where applicable. f(x) = x4 – 54x2 + 245 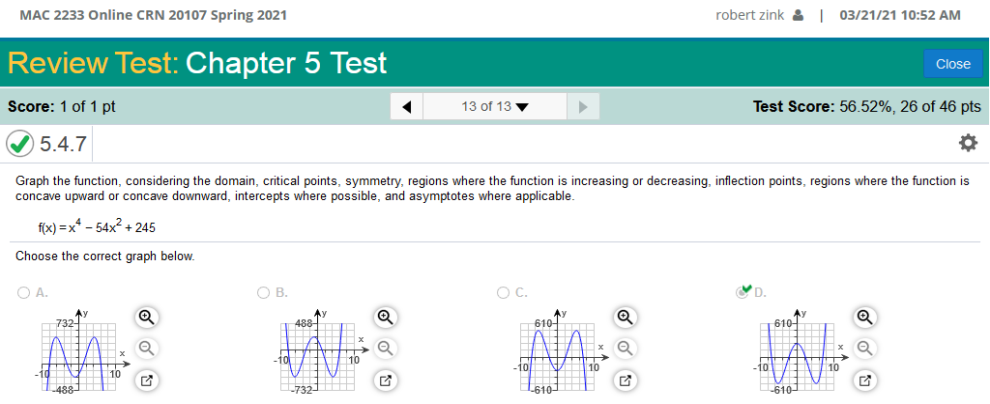
Explanation: Graph with points 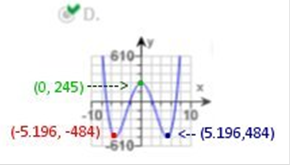 To solve this problem, we need to find the Local Minima and the Local Maxima This calculator will find and compare those to the graphs. (-5.196, -484) (0, 245) (5.196,484) You can find the Local Minima below. Enter the equation as shown below. https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/ 

The long way To find the local maxima, we need to find the derivative of the given equation. f(x) = x4 – 54x2 + 245. Again, after you start calculating derivatives, you will be able to do them quite easily. I can do this by eye. x4 = 4x3 - 54x2 = -108x 245 = 0 the derivative = 4x3 – 108x Next step is: Solve for x: 4x3 – 108x = 0 Answer: x = 0 or x = 5.196152422706632 or x = −5.196152422706632 We can now see that one of the points to plot is zero (0). Two of the graphs in question Have points plotted equal at 0. We are already given the y-value of 245 however, one of the graphs has values of 0, 245 and 0, -245, so we will find the y-value when x = 0. Plug in the x value of 0 into f(x) = x4 – 54x2 + 245 f (0) = (0)4 – 54(0)2 + 245 = 245 The Local Maxima is (0, 245) and only one of the graphs have those values plotted, so, we do not need to go any further and do not need to find the local minima. However, if we wanted to all we need to do is plug in one of the values we have already found which is (5.196152422706632) f(x) = x4 – 54x2 + 245 Plug in value of x: (5.196152422706632)4 - 54(5.196152422706632)2 + 245 = -484 Plug in value of x: (-5.196152422706632)4 - 54(-5.196152422706632)2 + 245 = -484 Local Minima: (-5.196, -484) Local Minima: (5.196, 484) We can now plot all the points! Homework Chapter 1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM | Need A Tutor? | Need Homework Help?
|
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |