|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Calculus For Business
Test 4 At the end of 8 years, the balance in the account is given by A = 2700.00 Find the rate of change of A with respect to r when r is 6.00%. 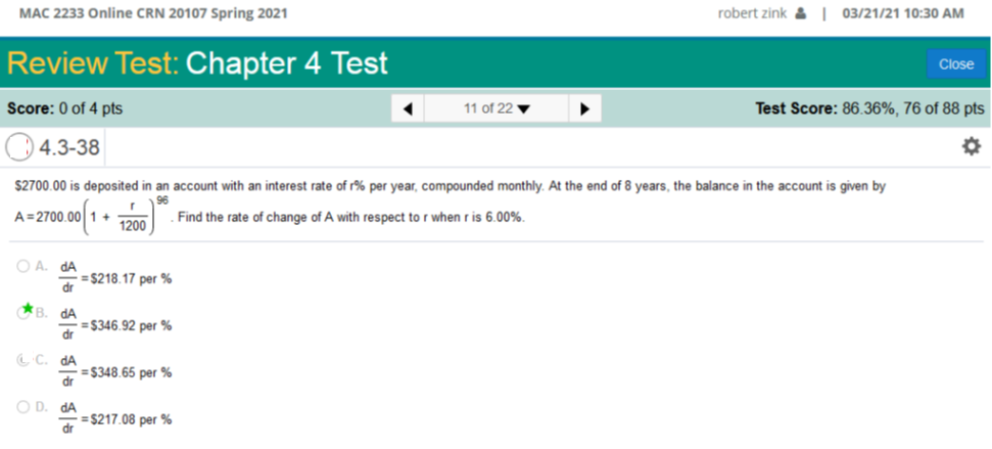
Use a scientific calculator and enter EXACTLY as shown below. You will need a calculator to solve this problem. 2700(96) ÷ 1200(1 + 6 ÷ 1200)95 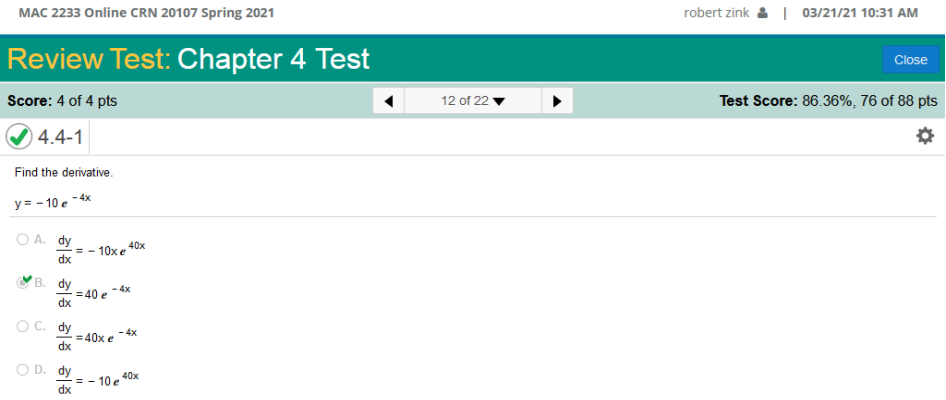
It is easiest to solve this the long way because it is not difficult. nn - 1 -10(e-4x · - 4x) -10 · -4x (e) = Answer = 40e-4x Find the derivative. 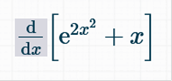
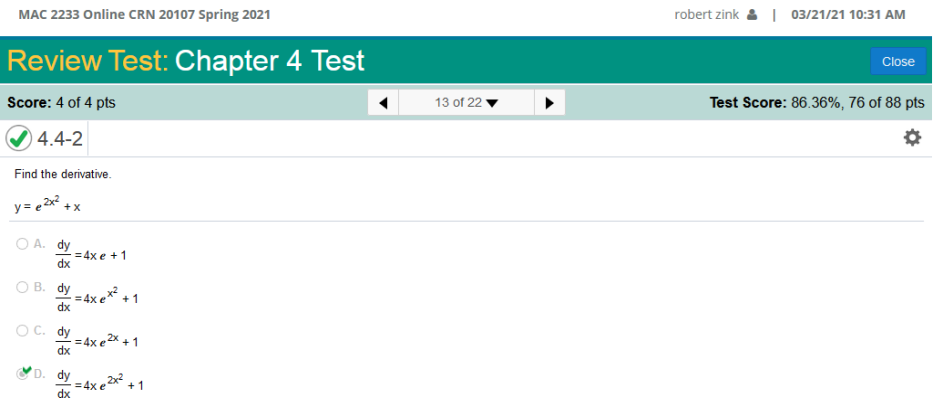
Explanation: Note: With this calculus problem, we split the equation up. The derivative of x is 0, so If you notice, this has a SECOND EXPONENT, so what we do here is we find the derivative of 2x2 and put that is front of e2x2 The derivative of 2x2 = 4x The answer is https://www.derivative-calculator.net/ You need to enter EXACTLY as shown or it will not be solved. 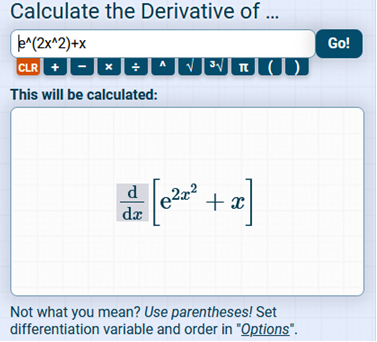
Find the derivative. y = 115x 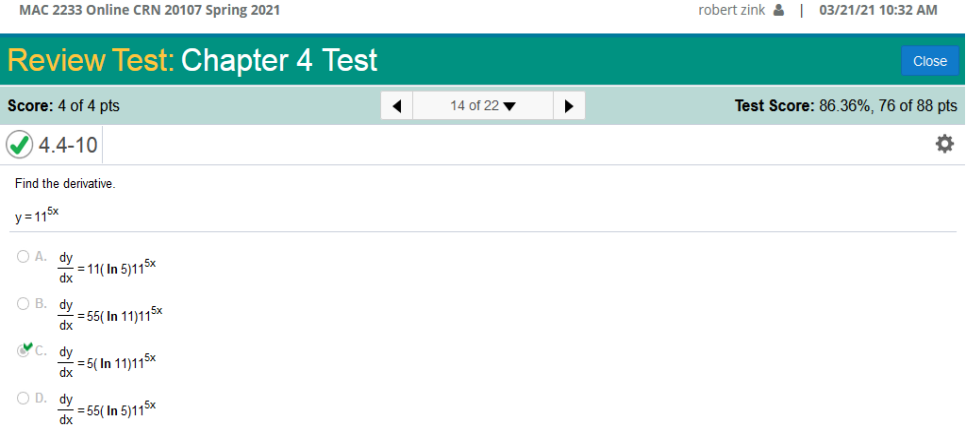
ln (11) · 115x · ln (11) · 115x · 5 · now we move the 5 in front and the derivative of x (which is really 1x) = 1 5 ln (11) · 115x · 1 11 · 1 = 11, so we can finalize the answer Answer = 5 (ln 11) 115x https://www.derivative-calculator.net/ You need to enter EXACTLY as shown or it will not be solved. 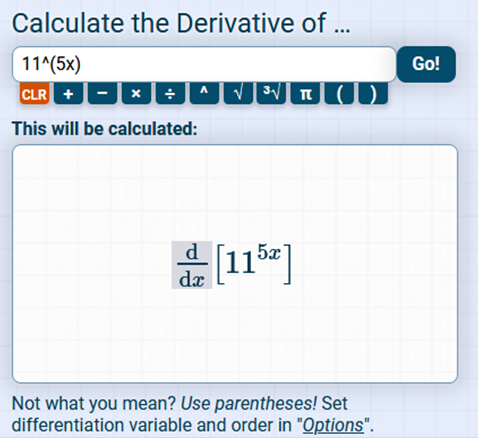
Find the rate of change of sales at the time when t = 6. Round to the nearest tenth. 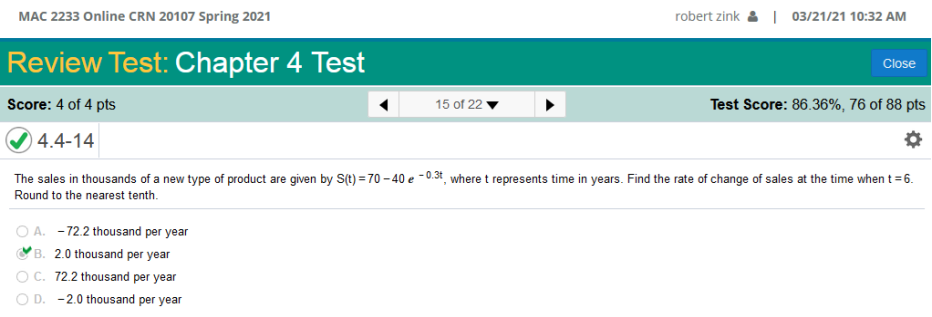
To solve this calculus problem, we must first know the value of e which is 2.71828. We need to plug these in after finding the derivative >> e = 2.71828 and t = 6 Next, we must find the derivative of 70 – 40 e-0.3t The derivative of 70 = 0 so we can eliminate the left side. To differentiate – 40 ( – 40 ( Now we simplify: 12 12 The derivative of 70 – 40 e-0.3t = 12e-3t/10 Then we must plug in the values of e = 2.71828 and t = 6 We can use a scientific calculator and enter the equation exactly as below. *Be sure to use the negative key on the calculator and not the minus sign! 12 (2.71828) (-3(6)/10) = 1.98358906 Round to the nearest tenth. Answer = 2.0 thousand per year. https://www.derivative-calculator.net/ You need to enter EXACTLY as shown or it will not be solved. 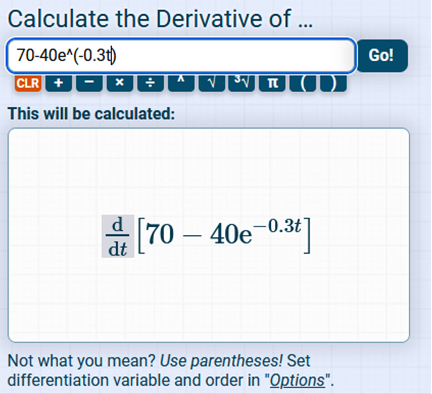
The demand function for a certain book is given by the function D(p) – 61 e 0.003p Find the marginal demand Upper D’(p). 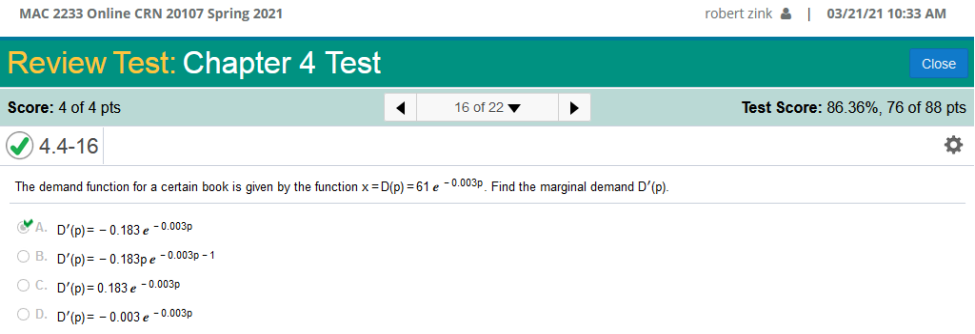
This has been discussed above. The marginal demand function is simply the derivative of the demand function. It is very simple in this case. We multiply -0.003 by 61 and keep the variables in place. -0.003p · 61e = -0.183e-0.003p The book will likely have you fill up an entire page to find the answer, But it is simple as that. As you can see, I had the correct answer! Suppose that the amount, in grams, of a radioactive substance present at time t, in years, is given by A(t) = 340 e-0.87t Find the rate of change of the quantity present at the time when t is 8. Round to the nearest tenth. 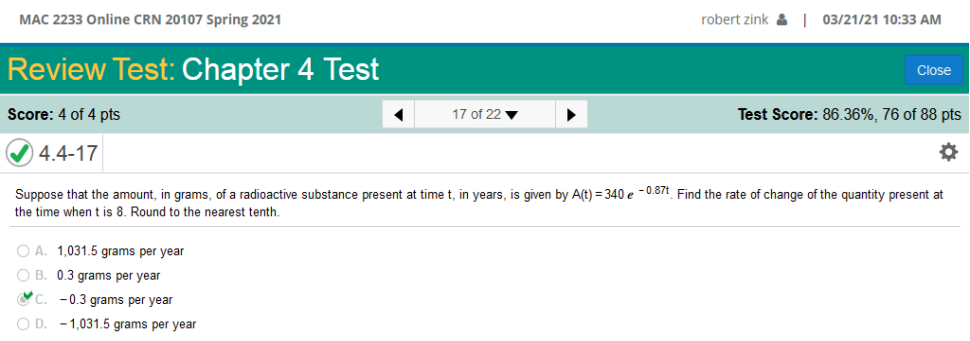
To solve this calculus problem, we must first know the value of e which is 2.71828. e = 2.71828 t = 8 We plug in the values and solve. 340(2.71828) · -(0.87 · 8) We can use a calculator to solve the equation above. 340(2.71828) -0.87(8) = .3226943461 Round to the nearest tenth. -0.3 *Note that the computed rate of change will be positive however, it must be negative in this case. Find the derivative of the function. y = ln 2x 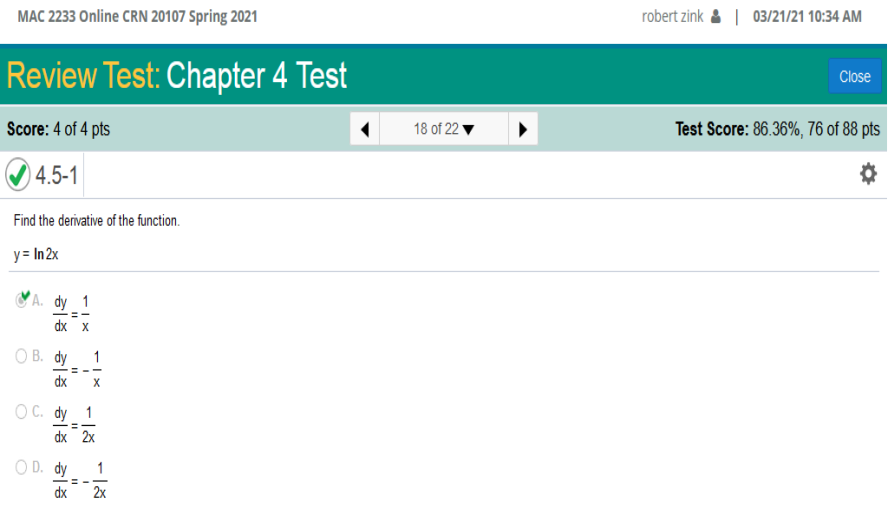
To apply the Chain Rule, set u as 2x / The derivative of ln(u) with respect to u is Since 2 is constant with respect to x, the derivative of 2x with respect to x is 2 We can now combine 2 and Now we can cancel the common factor / and the derivative of x = 1 https://www.derivative-calculator.net/ You need to enter EXACTLY as shown or it will not be solved. 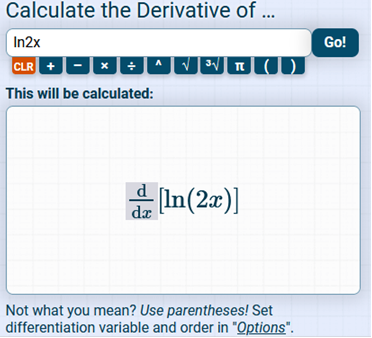
Find the derivative of the function. y = ln (6 + x2) 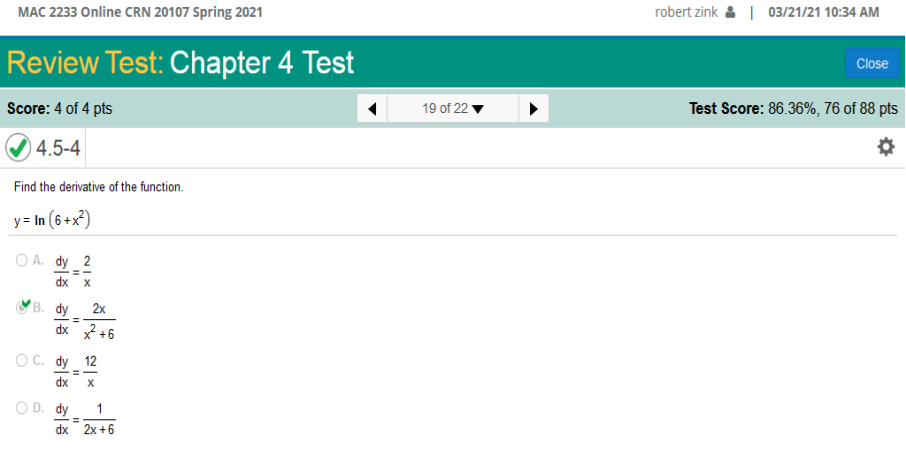
We will apply the Chain Rule and set u as 6+x2 The same as above: The derivative of ln(u) with respect to u is Next, we will replace all occurrences of u with 6 + x2 Now we can finalize the answer. First, let’s put the left side in proper order… We have https://www.derivative-calculator.net/ You need to enter EXACTLY as shown or it will not be solved. 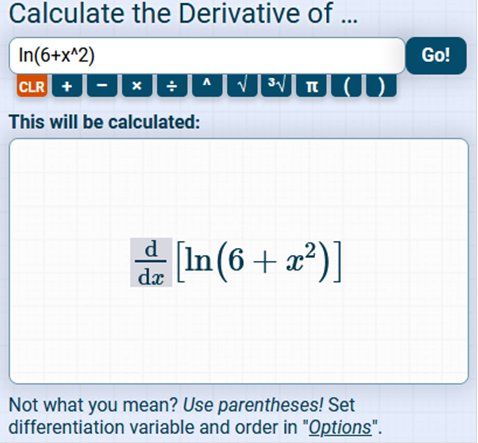
Find the derivative of the function. y = log (8x – 3) 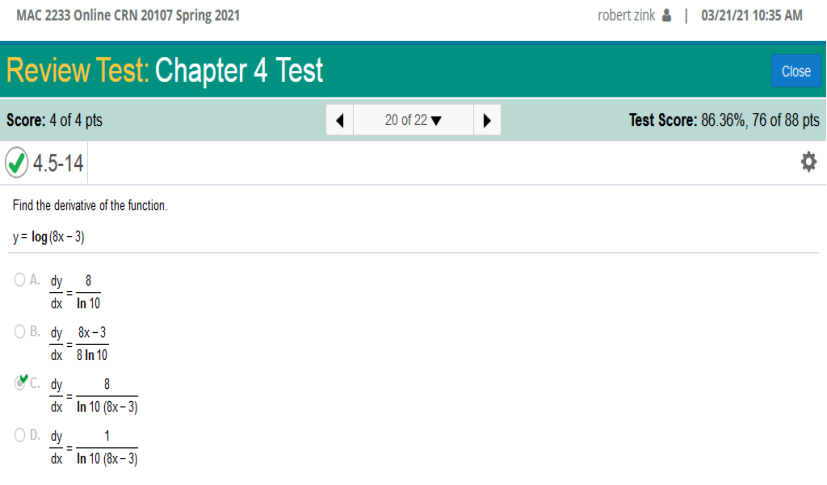
the long way. The derivative of log = Assume the total revenue from the sale of x items is given by R(x) = 21 ln (7x+1) while the total cost to produce x items is x/5 Find the approximate number of items that should be manufactured so that profit, R(x) – C(x), is maximized. 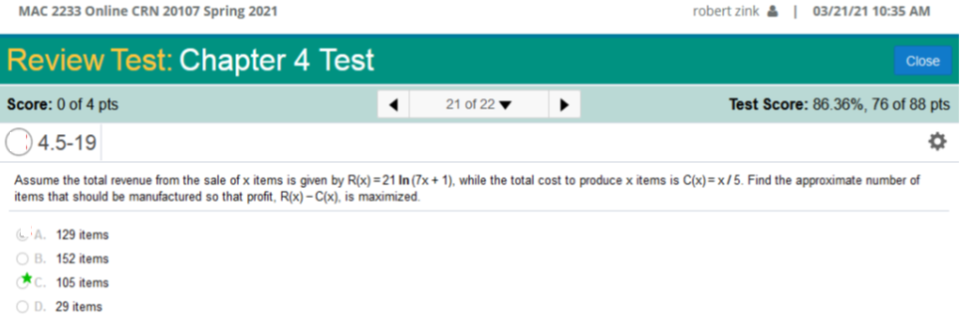
This is the easiest way to solve this problem. I wrote this equation and solved for x. If you look closely at the question, you will see how I set the values up. The long way is like so. It is a lot to follow but it is done like so. 21 ln (7x + 1) - 21 Solve for 0 Simplify 147 = Eliminate the fraction & Multiply 5 · 147 = 735 = 7x + 1 Subtract 735 – 1 = 734 = 7x 734 ÷ 7 = x x = 104.85714285 Given the multiple-choice answers we need to round up to 105. Suppose that the population of a certain type of insect in a region near the equator is given by P(t) = 17 ln(t + 12) where t represents the time in days. Find the rate of change of the population when t equals 2. Round to the nearest tenth as needed. 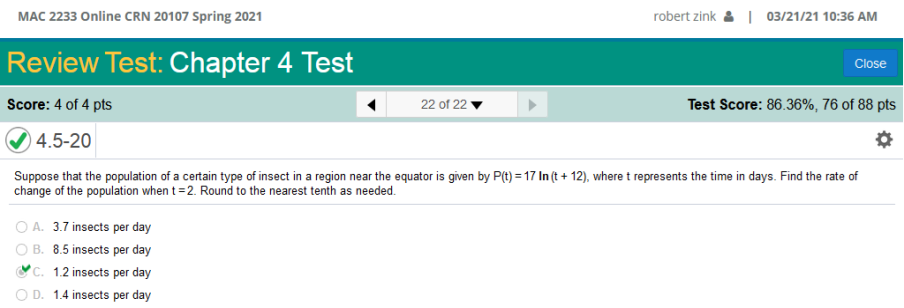
Find the derivative of 17 ln (t + 12) Then plug in the value t = 2 https://www.derivative-calculator.net/ You need to enter EXACTLY as shown or it will not be solved. 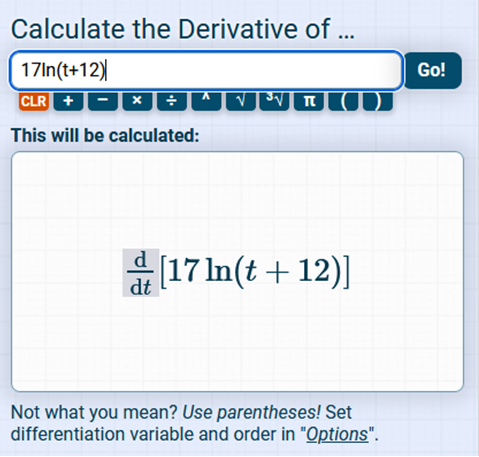
Homework Chapter 1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM | Need A Tutor? | Need Homework Help?
|
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |