Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel

Complete the table and use the result to find the indicated limit.
 

 
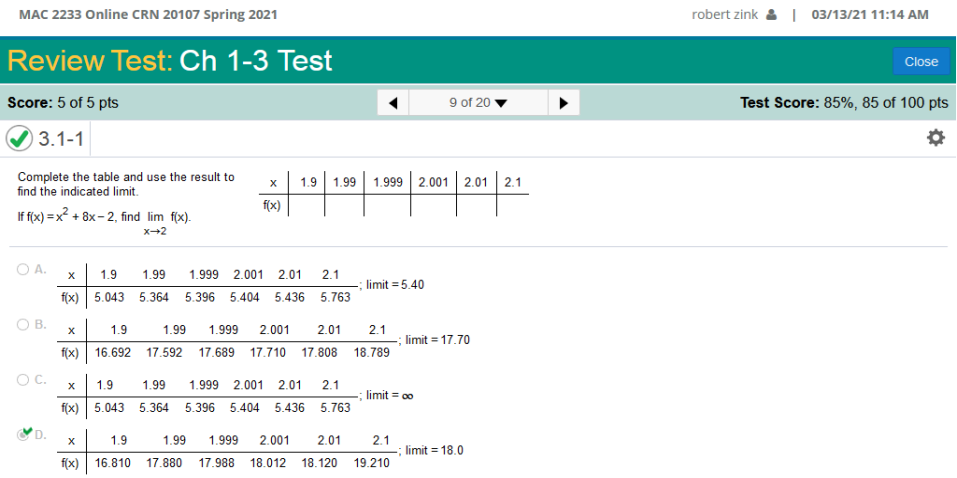
Solution
(1.9)² + 8(1.9) – 2 = 16.810
(1.99)² + 8(1.99) – 2 = 17.880
and so on
   
Complete the table and use the result to find the indicated limit.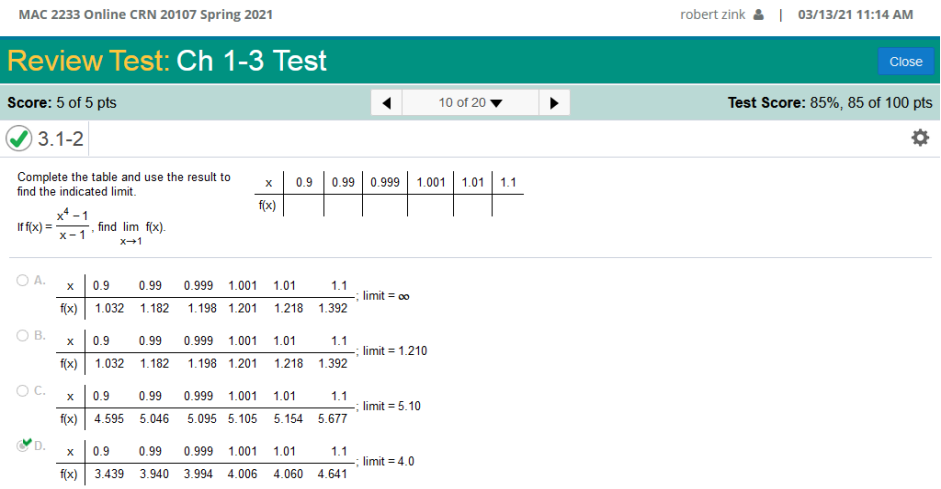
 

 
Solution
Enter in ti-nspire or ti84 plus exactly like so
(.9⁴ – 1) ÷ (.9 – 1) = 3.439
(.99 - 1) ÷ .99 – 1) = 3.940
And so on…
   
Use the properties of limits to help decide whether the limit exists.  If the limit​ exists, find its value.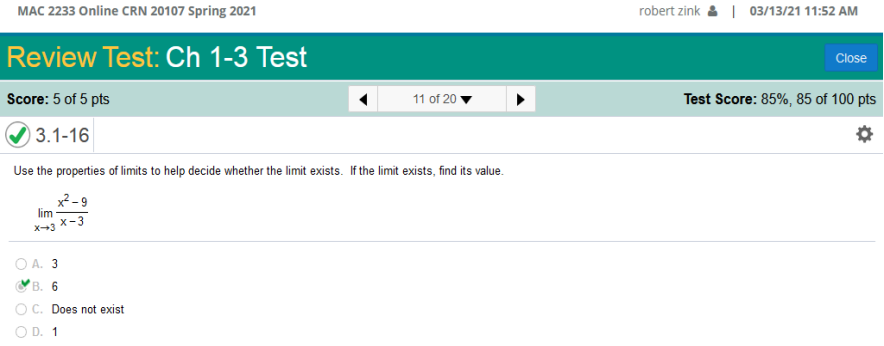
 

 
Solution
Simplify
x² – 9 / x – 3     =     x / x² = x    and     -9 / -3 = 3
Now put the equation back together = x + 3
Now plug in the value of
x --> 3
(3) + 3 =             6
   
Use the properties of limits to help decide whether the limit exists.  If the limit​ exists, find its value.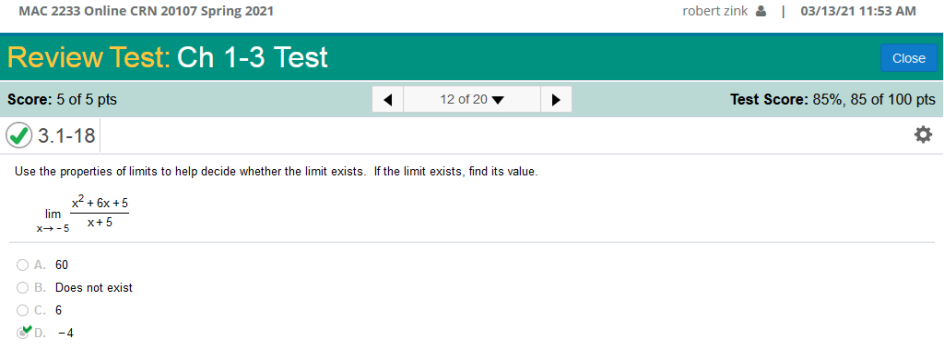
 

The Ti-nspire will solve this problem if you are allowed to use it.
Otherwise, solve like so
 
Solution
Simplify
 

 
x + 6 + 5
 

 
x + 1
Now plug in the value of (x à-5)
1 – 5 = -4
   
Use the properties of limits to help decide whether the limit exists.  If the limit​ exists, find its value.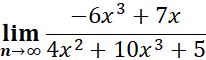

 

 
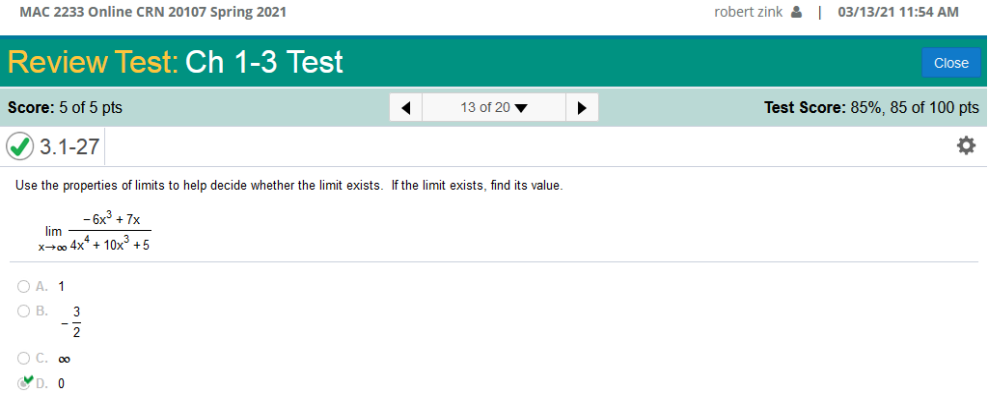
Solution
divide by the highest denominator power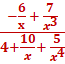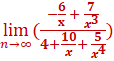
 =   
 
 = 0   ) = 4        =      = 0
   
Use the properties of limits to help decide whether the limit exists.  If the limit​ exists, find its value.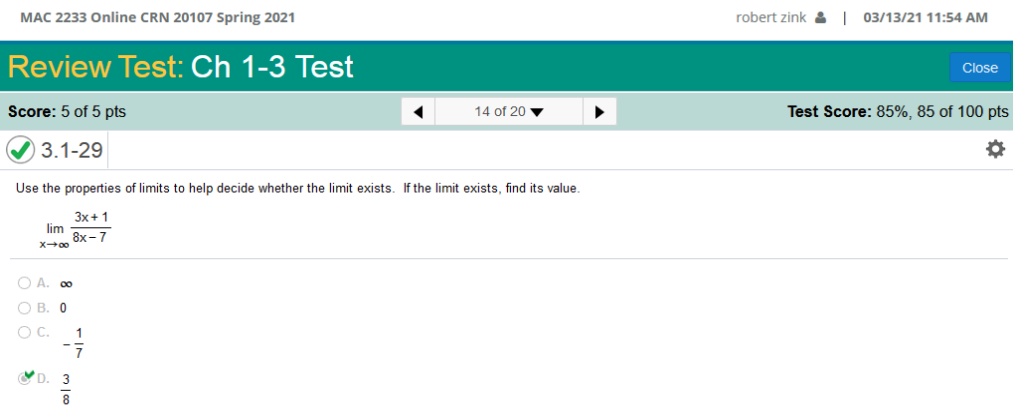
 

 
Solution
divide by the highest denominator power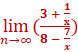
 =          
 (3 + ) = 3          (8 + ) = 8 =
  The cost of manufacturing a particular videotape is c(x) = 10,000 + 7x where x is the number of tapes produced.
The average cost per​ tape, denoted by c (x) is found by dividing c(x) by x.
            Find     lim    c(x)
                   x--> 2.000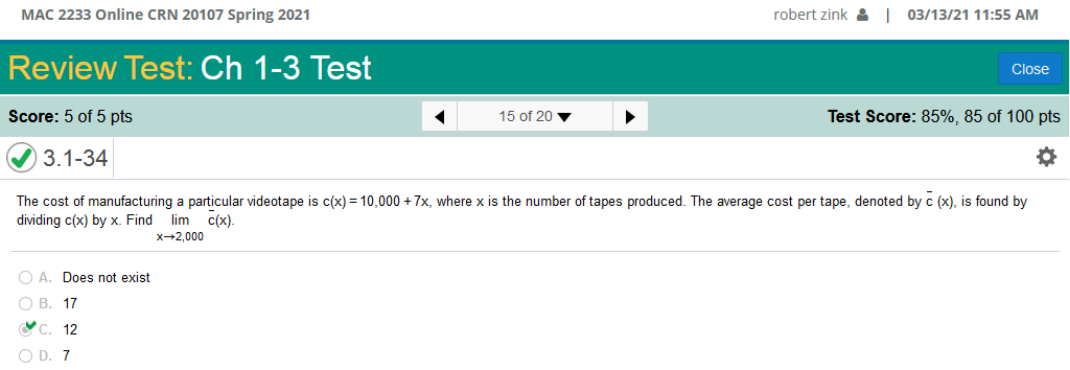
 

 
The equation we need to write is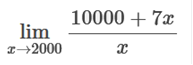


 
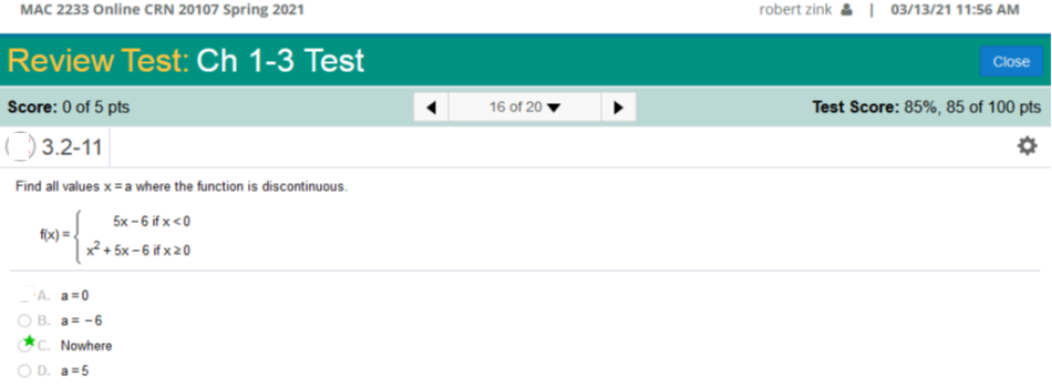
Then we plug in all the values of
x = 2,000
10,000 + 7(2,000) ÷ 2,000
10,000 + 14,000 ÷ 2,000
24,000 ÷ 2,000 = 12
   
Find all values x = a where the function is discontinuous.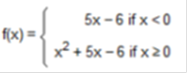

 

   
Find the average rate of change for the function over the given interval.
y = x² + 4x between x = 4 and x = 8.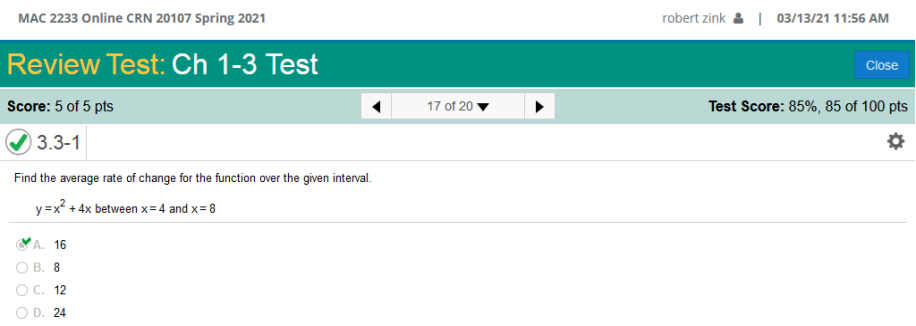

 
Solve the long way…
 

 
64 + 32 – 16 + -16 = 96 – 32 = 64
64 / 8 – 4 =      64 / 4 = 16
 
Or
 
This is a cool online calculator that will solve this problem for you.
https://www.emathhelp.net/calculators/calculus-1/average-rate-of-change-calculator/
enter equation and points.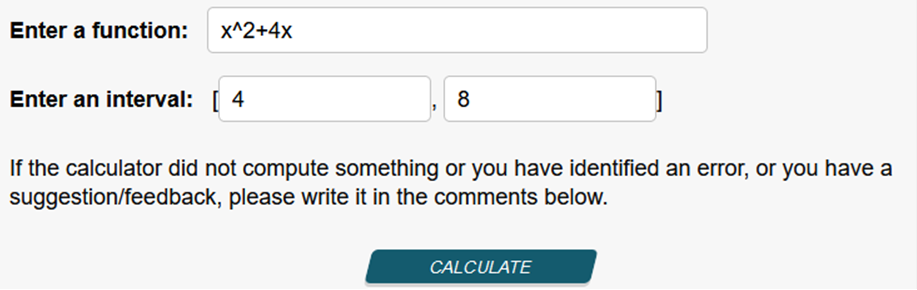

   
Find f’(x) at the given value of x.
f(x) x² – 9x + 2, find f’(- 4​).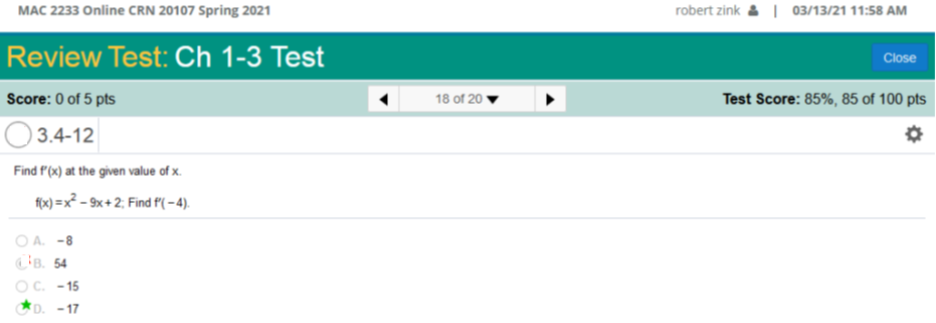
 

 
Solve the long way…
n^n-1 (n = the exponent)
If a variable has no exponent, then the variable is cancelled out.
For example, with 2x, the derivative would = 2 because the exponent is equal to ¹ and ^n-1 would cancel it out.
If a number in an equation has no variable, then the derivative = 0.
What I do is I always do is multiply a number with no variable by 0 when finding the derivative.
For example, 1, the derivative = 0 (you do not need to represent the 0)
 So, the derivative of x² – 9x + 2 is:
 
2(x^{2 – 1}) – 1(9^{1 – 1}) + 2(0)
2x – 9
2(-4) – 9 = -8 – 9 =
-17
 
Or
 
This calculator will find the derivative for you.
 
https://www.derivative-calculator.net/
 

   
Using the definition of the​ derivative, find f’(x). Then find f’(1), f’(2) and f’(3) when the derivative exists.
    f(x) = -x² + 9x - 4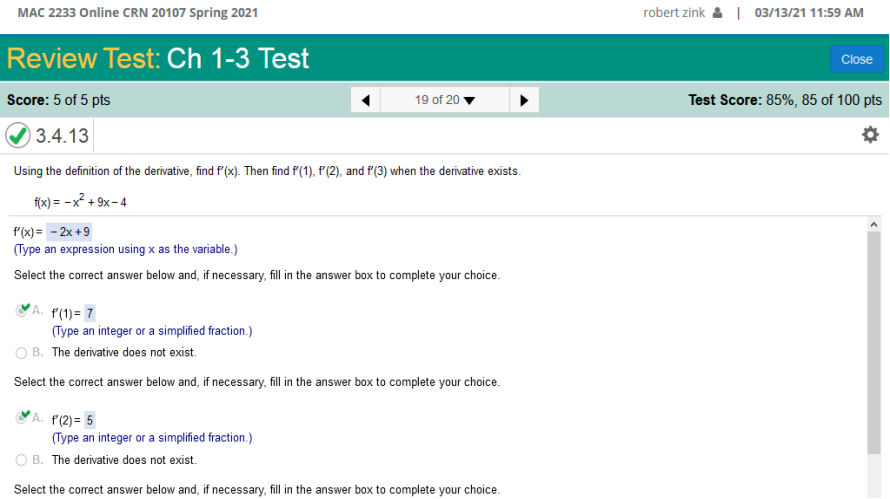
 

 
Solve
 
Find the derivative of
f(x) = -x² + 9x – 4 (which is -2x + 9)
and plug in the values of f’(1) which is 1, f’(2) which is 2 and f’(3) which is 3.
This is the same as above, except you need to find the derivative and find multiple values for f’().
solve the long way.                n^n-1 (n = the exponent)
The same rules apply as above.
n^n-1(-x² + 9x – 4) =       2(x^{2 – 1}) + 9(x^{1 – 1}) – 4(0) =        -2x + 9
Now plug in all the values of f’() which are 1, 2, & 3.
-2(1) + 9 = -2 + 9 = 7
-2(2) + 9 = -4 + 9 = 5
-2(3) + 9 = -6 + 9 = 3
 
This calculator will find the derivative for you.
https://www.derivative-calculator.net/
and enter in the equation as so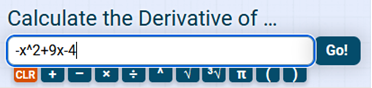
 

  Suppose the demand for a certain item is given by D(p) = -4p² + 3p + 7 where p represents
the price of the item. Find the rate of change of demand with respect to price.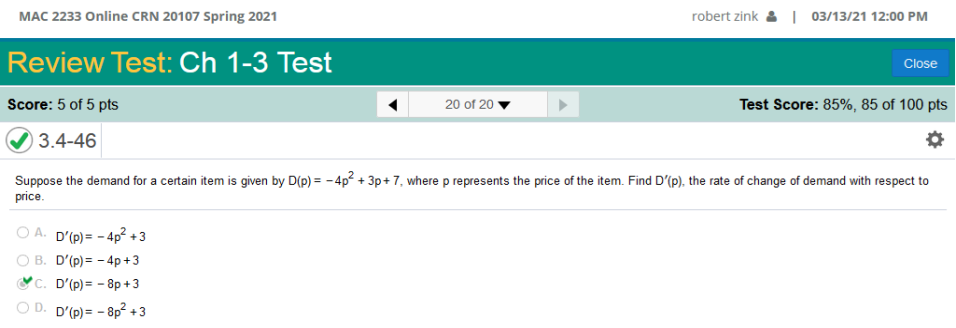


 
We need to find the demand which is simply the derivative in this case.
The book gave long lessons on finding the demand however after I solved about
a dozen of the problems, I came to realize that the demand was simply the
derivative of the expression and the variable used is p instead of x.
Imagine the time I saved after that!
 
Find the derivative of -4p² + 3p + 7 =            -8p + 3
The same rule applies as above.
 
n^{n – 1}(-4p² + 3p +7) =
2(-4p^{2 – 1}) + 3(p^{1 – 1}) + 7(0)
D’(p)-8p + 3
 
It is as simple as that!

---

---