Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel

Homework 7.1
the difference between a definite integral and an indefinite integral is:
Definite Integral contains upper and lower limits and an indefinite integral does not.
Indefinite integrals, which we are working on first in this lesson, will usually not have an answer with a number value and will
contain variables and exponents.
Definite integrals will usually have an answer that has a number value, because upper and lower limits are giving values
to the variables.
indefinite integral  + C

 
Evaluate the following indefinite integral.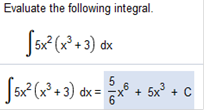
² (x³ + 3) dx

The formula for Indefinite Integrals is  + C

Please note: x in this case is 0x not 1x.
x in this case can be somewhat confusing because we will be adding x,
However, we will be adding 0x. In Intermediate and College Algebra x + x would be 1x + 1x = 2x.
 + C [² (x³ + 3) dx]

First, we need to factor ² (x³ + 3)

5x²(x³) = 5x⁵ and 5x²(3) = 15x² =         5x⁵ + 15x²
Now we have  + C [5x⁵ + 15x²]

We will evaluate each expression separately to make it easier to understand.

Now we need to         ² (x³ + 3) dx
 + C [² (x³ + 3) dx]

First, we need to factor ² (x³ + 3)

5x²(x³) = 5x⁵ and 5x²(3) = 15x² =         5x⁵ + 15x²
Now we have  + C [5x⁵ + 15x²]

N is the same as it is with Derivatives.
N = the exponent in the equation we are trying to solve.
So, what we do with 5x⁵ and  is, we fill in x and the exponents.

x in this case is 5 and it just so happens that n is 5 also so we will use () to fill in.
 and now we have the first part of the solution.

 =  or x⁶
 
We have 15x²
we simply plug in the values into our formula.
   > 15x²  >  

Now we can simplify this expression because x is separated.
15 / 3 = 5 so we are left with 5x³
Now we can put part 1 and part 2 together and add c. C is added to an indefinite integral because it is continuous.
We are not given upper and lower limits, so we have no values for the variables. It is continuous.
The answer is x⁶ + 5x³ + C
Incidentally, the online calculators would give us an answer that looks something like this. ³ + 3)² + C which is a mess.
   
Find the indefinite integral 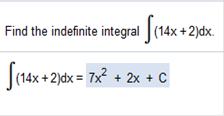  (14x + 2) dx

 dx
 + C
 
   =      + C = 7x² (simplified)
 
 =  = 2x
 
The answer = 7x² + 2x + c  
Evaluate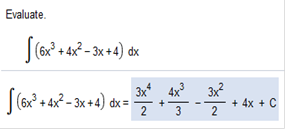
(6x³ + 4x² – 3x + 4) dx
 

 + C
 
 =       =        
 
 =     
 
 =  -
  Evaluate
∫ (9x² − 7x + 5) dx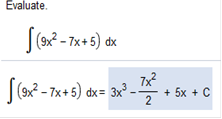

∫ 9x² =              = simplify to 3x³
∫ -7x =           

∫ 5 =                  5x
Solution:         3x³ 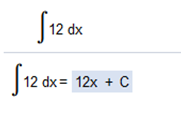 + 5x + C
  Evaluate

Apply the constant rule….
  Evalu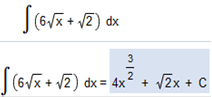ate
∫ (6√x + √2)dx
 
       
Rewrite as 6 ∫ √x + √2 + C
We can convert √x as x^1/2
the integral of x^1/2 is              ^3/2 
the integral of √2 is               √2       
so, we have    6 ∫  ^3/2 + √2x + C
6 ∫  ^3/2 =     4x^3/2
The answer is 4x^3/2 + √2x + C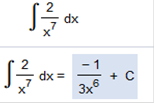   
 

We rewrite as             2 ∫ 
 
We can rewrite           as              x^-6
 
Now the power rule     and    x^-6 =     x^-6
 
Now we have 2 ∫ x^-6 or (x^-6)
 
Now we move x^-6 to the denominator, and it is positive
( =  and simplify  + C
   
Find the cost function if the marginal cost function is C’(x) = 3x – 5 and the fixed cost is $11.

Find the integral of 3x – 5 (be sure to move the x over next to the fraction)
Then add 11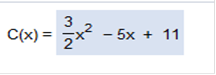
 

 + C = (+ C will not be required, because 11 is the fixed cost)
 
3x =     3/2x²
 
-5 =      5x
 
Fixed cost = 11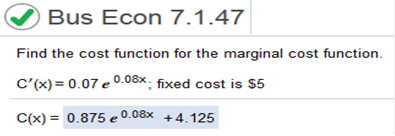
 
x² – 5x + 11
  Find the cost function for the marginal cost function. fixed cost is $5.
 

 
To evaluate remove all values and evaluate as below.

.07 / 1(1/08) = .07/.08 = .875             Subtract 5 - .875 = 4.125
 
Now set up the equation by putting the values back in place.
0.875 e^0.08x + 4.125
   
Find the cost function for the marginal cost function.
C’(x) = 7x – 5/x; 10 units cost 279.54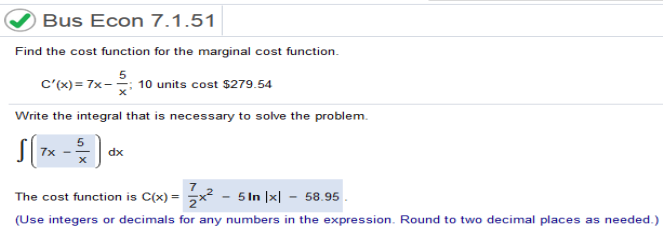
 

 
Find the integral of 7x – 5/x =
7/2x² – 5ln (|x|) (plug in the units (10))
7/2(10)² – 5 ln (|(10)|) =        338.48707453503 (is negative)         + 279.54 = -58.9471 = round to 2 decimals     58.95
Set up the equation by using the integral
7/2x² – 5 ln (|x|) - 58.95
   
Find the demand function for the marginal revenue function. Recall that if no items are​ sold, the revenue is 0.
R’(x) = 0.03x² – 0.04x + 195
 

 
Find the integral of 0.03x² – 0.04x + 195
then divide by x (subtract 1 exponent from the top)
.01x³ - .02x² = 195x / x
  The approximate rate of change in the number​ (in billions) of monthly text messages is given by the equation.
 
 

Find the integral 0f 7.2t – 16.2 =       3.6² -16t
plug in t = 3
3.6(3)² – 16(3) = -16.2 + -9.4 = positive value           25.6
Combine with integral.
3.6t² – 16.2t + 25.6
   
The number of​ bachelor's degrees conferred has been increasing steadily in recent decades.
The rate of change of the number of​ bachelor's degrees​ (in thousands) can be approximated by the following function where t is the number of years since 1970.
B’ (t) = 0.0612t² – 1.968t + 1516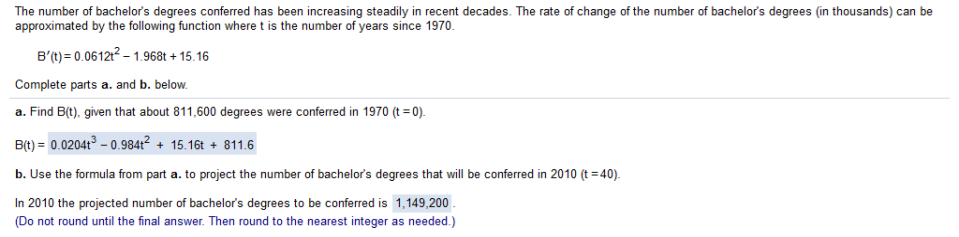

a.      Find the integral of
 

  Simplify
  to 811.6 and add it to the integral

b.       plug in 40 and 3 zeros
  Homework 7.2 The marginal revenue​ (in thousands of​ dollars) from the sale of x gadgets is given by the following function.
 

 
find the integral…
6(x² + 29000)^1/3
Then divide the given gadgets by 1000 = 18.933 and subtract the integral
18.933 – 6(x² + 29000)^1/3
 
Plug in the 115 value in and solve.
18.933 – 6(115² + 29000)^1/3 = -190
Then subtract from the equation
6(x² + 29000)^1/3 -190
 
Divide the revenue of 40,000 by a thousand = 40
Solve 6(x² + 29000)^1/3 – 40 for x.
Round up to the next whole dollar.
   
An epidemic is growing in a region according to the rate.
a.      Find the formula for the number of people infected after t days, given that 64 people were infected after t days.
b.      Use the answer from part a to find the number of people infected after 26 days.

 
a. Find the integral.
Plug in 0 for t and subtract it from 64 then
Use the integral and add the results.
 
b. plug in 26 for t into the equation and solve.
  Homework 7.3 Explain the difference between an indefinite integral and a definite integral.
 
C. A definite​ integral, after evaluating it at the limits of​ integration, results in a particular number.
An indefinite integral results in a set of functions that share the same derivative and uses an arbitrary constant of integration.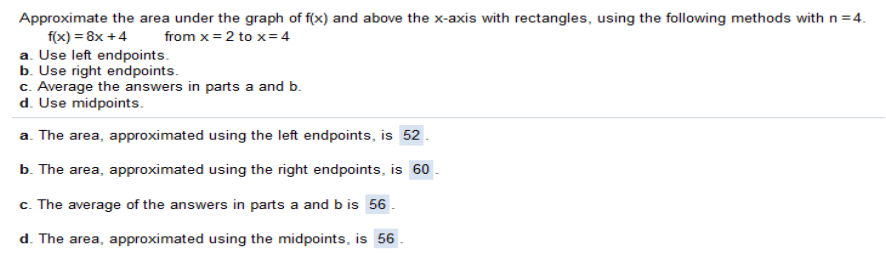
  Approximate the area under the graph of​ f(x) and above the​ x-axis with​ rectangles, using the following methods with N = 4

 
a)) 8(2) + 4(.5) + 8(2.5) + 4(.5) + 8(3) + 4(.5) + 8(3.5) + 4(.5) =          52
b)) 8(2.5) + 4(.5) + 8(3) + 4(.5) + 8(3.5) + 4(.5) + 8(4) + 4(.5) =          60
c)) 52 + 60 / 2 =           56
d)) Midpoint is 2 + 2.5 / 2 = 2.25       8(2.25) + 4(.5) + 8(2.75) + 4(.5) + 8(3.25) + 4(.5) + 8(3.75) + 4(.5) =             56
 
Check
https://www.emathhelp.net/calculators/calculus-2/riemann-sum-calculator/
use left and right endpoints from the dropdown menu
  Approximate the area under the graph of​ f(x) and above the​ x-axis with​ rectangles, using the following methods with n = 4.
f(x) = -x² + 4 from x = -2 to x = 2

https://www.emathhelp.net/calculators/calculus-2/riemann-sum-calculator/
 
a)) -(-2)² + 4 (1) + -(-1)² + 4 (1) + -(0)² + 4(1) + -(1)² + 4(1) = 10
b)) -(-1)² + 4 (1) + -(0)² + 4(1) + -(1)² + 4(1) –(2)² + 4 = 10
c)) 10 + 10 / 2 = 10
d)) -(-1.5)² + 4 (1) + -(-.5)² + 4(1) + -(.5)² + 4(1) –(1.5)² + 4 = 11
  Approximate the area under the graph of​ f(x) and above the​ x-axis with​ rectangles, using the following methods with n = 4.
 
f(x) = e^x + 3      from x = -2 to x = 2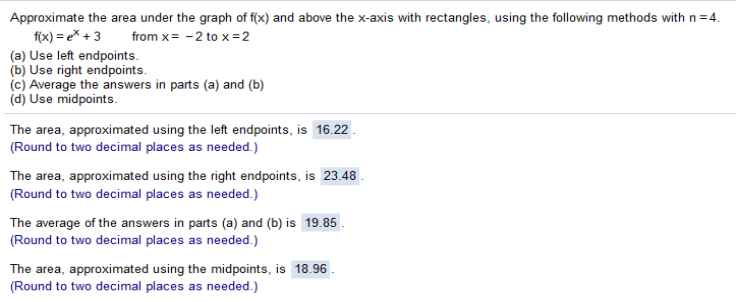
 

 
a)) e^-2 + 3 (1) + e^-1 + 3 (1) + e⁰ + 3 (1) + e¹ + 3 (1) = 16.22
b)) e^-1 + 3 (1) + e⁰ + 3 (1) + e¹ + 3 (1) + e² + 3 (1) = 23.48
c)) 16.22 + 23.48 / 2 = 19.85
b)) e^-1.5 + 3 (1) + e^-.5 + 3 (1) + e^.5 + 3 (1) + e^1.5 + 3 (1) = 18.96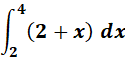
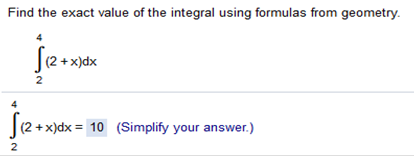
  Find the exact value of the integral using formulas from geometry.


 (2 + x) = x² + 2x
 
x² + 2x
 
Upper Limit b = 4
Lower limit a = 2
We need to plug in the limits, and then subtract b - a
16 + 8 – 0.5(2) – 2(2) The speed of a particle in a test laboratory was noted every second for 3 seconds. The results are shown in the following table. Use the left endpoints and then the right endpoints to estimate the total distance the particle moved in the first three seconds.
 

 
9(1) + 5.5(1) + 5(1) = 19.5
5.5(1) + 5(1) + 3.5(1) = 14 Watch the Area and the Definite Integral video and then answer the question given below.
What is the marginal​ cost?
Click here to watch the video.
 
Choose the correct​ description(s) of marginal cost. Select all that apply.
 
B. The derivative of the cost function
C. The cost per item Watch the Area and the Definite Integral video and then answer the question given below.
What would the marginal cost at 100 units tell​ you?
Click here to watch the video.
Choose the correct description of the marginal cost at 100 units.
The cost of the 101st phone Homework 7.4 Evaluate the integral.
 
 
Apply the constant rule.
6x]5,3
Evaluate 6x at 5 and at 3.
(6 x 5) – 6 x 3
30 − (6 x 3) = 12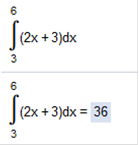
   

First we find the antidiverative
 + 3x

Upper Limit b = 6
Lower limit a = 3
We need to plug in the limits, and then subtract b - a
 
 + 3(6) -  + 3(3)
 
 + 18 -  + 9
 
3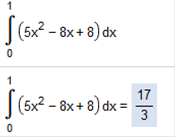6 + 18 – 9 + - 9
36
   

 
First we find the antidiverative which is
x³ – 4x² + 8x (we do not need to add + C)
 
So we have  x³ – 4x² + 8x

We have a fraction, so we will find a common denominator first. (which is 3)
 
x³ - x² + x
 
NOW, the easiest way to do this is move the variables and exponents to the top.
Then we plug in the upper limit. Since the lower limit is zero (0), we do not need to do
anything with that, because it will factor to zero(0). It cancels out!
 So now we have
 
 -  +  we plug in the upper limit 1.
 
 -  +  (we must remember the the exponents pertain to the upper and lower limits)
 
5(1)³ = 5          12(1)² = 12                  24(1) = 24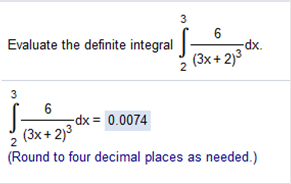
 
 -  +  =         
 
The antidevirative  = -

Now we plug in the value of the upper limit (3)
- = -0.00826446

Now we plug in the value of the lower limit (2)
- = −0.015625
 
Then we subtract
−0.00826446 - −0.015625 = 0.00736054       (0.0074)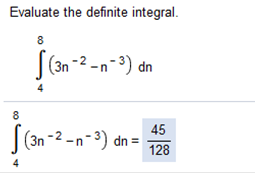  
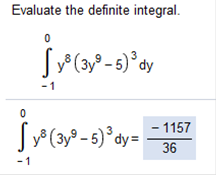
     Consider the region below f(x) = (13 – x) above the​ x-axis, and between x = 0  and x = 13.
Let x1 be the midpoint of the with subinterval.
Complete parts a. and b. below
 

 
a)) Approximate the area of the region using thirteen rectangles. Use the midpoints of each subinterval for the heights of the rectangles.
https://www.emathhelp.net/calculators/calculus-2/riemann-sum-calculator/

function: 13 – x
lower limit: 0
upper limit 13

Number of rectangles: 13
Type: Midpoint Rule
 
b)) Find Integral.
   
Find the area of the shaded region.

 
Solve 121 – x² = 0,x
x = 11, y = 0
so the two subintervals are x = 11, y = 12
 
integrals
f 11,0 (121 – x²) + f 11,12 (121 – x²)
2662 / 3 + 34 / 3 = 2696 / 3 The 2000 census in a particular area gives us an age distribution that is approximately given​ (in millions) by the function.
where x varies from 0 to 9 decades. The population of a given age group can be found by integrating this function over the
 interval for that age group.
f(x) = 40.6 + 2.08 – 0.84x²
 

= 246 (rounded)
 
What does this integral​ represent?
The total number of people in this area aged 0 to 90 was about 246 million in 2000.
  Homework 8.2 Find the average value of the function on the given interval.
f(x) = x² – 6; [0,7]
 

b = 7, a = 0
1 / b - a f b,a (x² - 6)
1 / 7 – 0 = 1/7 f 7,0 (x² – 6)
1/7 f 7,0 (x² – 6) = 31/3
  Find the average value of the function on the given interval.
f(x) = x² – 5; [0,6]
 

We need to solve this integral.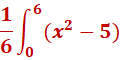

  Find the average value of the function on the given interval.
1/5  f 5,0 (√x + 5)

We need to solve the integral below

   
Find the average value of the function on the given interval.
f(x) = e^x/8; [4, 5]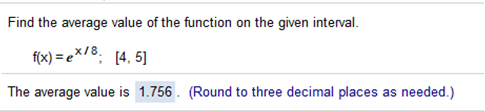

 
We need to solve the below integral in decimal Form
 = 1.75619
   
A stock analyst plots the price per share of a certain common stock as a function of time and finds that it can be approximated by the function
S(t) = 50 + 14 e^-0.07t, where t is the time​ (in years) since the stock was purchased. Find the average price of the stock over the first five years.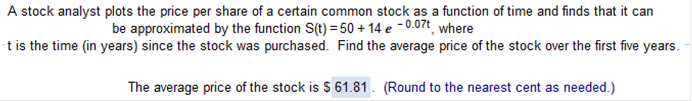
 

 
1 / b-a f b, a (equation)
1 / 5 – 0 = 1/5
 
1/5 f 5, 0 (50 + 14 e^-0.07t) dt = 61.81

---

---