Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel

Find the absolute maximum and minimum values of each function over the indicated​ interval, and indicate the​ x-values at which they occur.
 

 
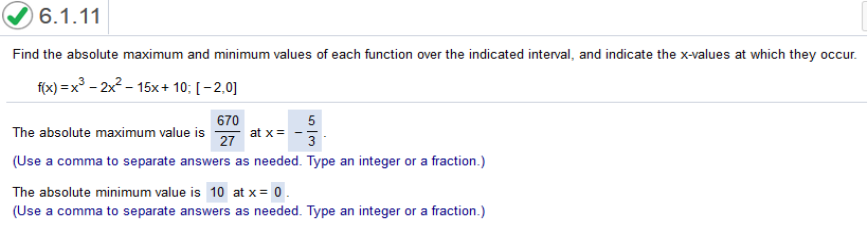
Long way
Find the derivative | solve for 0 and x | plug in the values of x
 
https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/
enter equation.
Global (Absolute) Minima (1^st is x) (0,10)
Global (Absolute) Maxima (1^st is x) (−5/3,670/27)
  Find the absolute extrema if they​ exist, as well as all values of x where they​ occur, for the function
1/3x³ -3/2x²- 4x + 4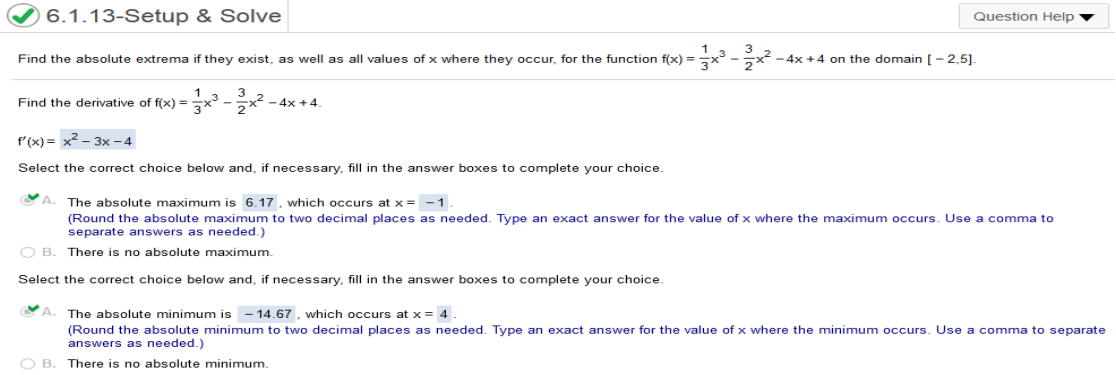
 

 
Long way
Find the derivative | solve for 0 and x | plug in the values of x
 
https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/
Enter a function of one variable: 1/3x^³-3/2x^2-4x+4
Enter an interval: [-2,5]
 
Global (Absolute) Maxima (use decimals and round if required) x is the 1^st number
Global (Absolute) Minima (use decimals and round if required) x is the 1st number
  Find the absolute maximum and minimum values of the following function over the indicated​ interval,
and indicate the​ x-values at which they occur.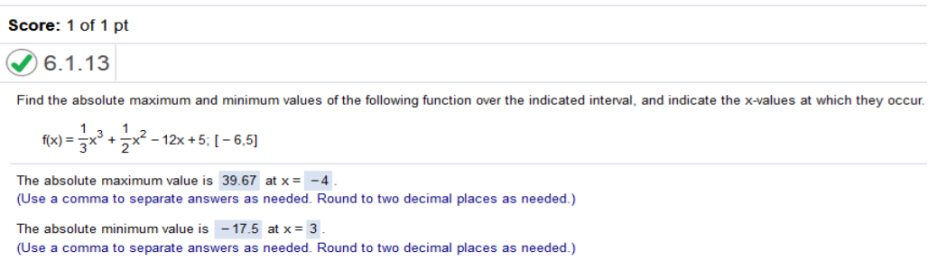

Long way
Find the derivative | solve for 0 and x | plug in the values of x.
 
https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/
Enter the equation
Global (Absolute) Maxima (use decimals and round if required) x is the 1st number
Global (Absolute) Minima (use decimals and round if required) x is the 1st number
  Identify the absolute extrema of the function and the​ x-values where they occur
 
Long way
Find the derivative | solve for 0 and x | plug in the values of x.
THERE IS NO MAXIMUM BECAUSE THERE IS ONLY 1 SOLUTION FOR X.
 

https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/
enter the equation.
For x > 0 enter (0,inf)
  The total profit Upper P(x) (in thousands of​ dollars) from the sale of x hundred thousand pillows is approximated by
P(x) = -x³ + 12x² + 144x – 400, x ≥ 5

Long way
Find the derivative | solve for 0 and x | plug in the values of x.
Add zeros for it is in thousands.
Add 5 zeros to the maximum x for maximu7m profit
https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/
enter the equation.
Global (Absolute) Maxima
The maximum profit is y and add 3 zeros.
The maximum profit will occur is x and add 5 zeros.
  Find the minimum value of the average cost for the given cost function on the given intervals.
x³ + 36x + 128
 

Find the derivative.
x² + 36 (then add 128/x and subtract 3 from 3x²)
 x² + 36 + 128/x
then enter the equation
https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/
Local Minima
The answer is y
84
Then plug in 10 into the equation
x² + 36 + 128/x
(10)² + 36 + 128/(10)
   
Follow the steps below to find the nonnegative numbers x and y that satisfy the given requirements.
Give the optimum value of the indicated expression. Complete parts​ (a) through​ (f) below.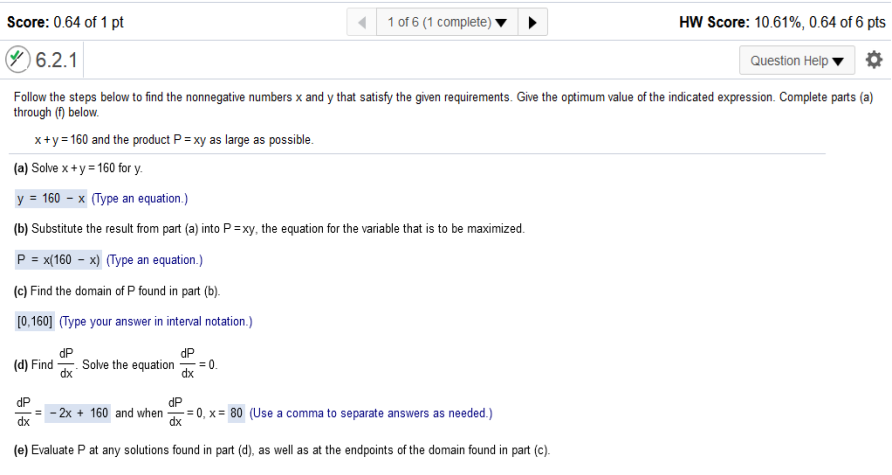
 

a.      y = 160 – x
b.      p = x(160 – x)
c.       y ≥ 0
160 - x ≥ 0
x ≤ 0
[0,160]
d.      p = x(160 – x) = -x² +160x
find derivative of -x² +160x
-2x + 160, set to 0 and solve for x
-2x + 160 = 0 = 80 x = 80
e.      –(80)² +160(80) = 6400 + 160(80) simplify
  Determine the average cost function C(x) = C(x) / x. To find where the average cost is​ smallest, first calculate C(x),
the derivative of the average cost function. Then use a graphing calculator to find where the derivative is 0.
Check your work by finding the minimum from the graph of the function Upper C overbar left parenthesis x right parenthesis.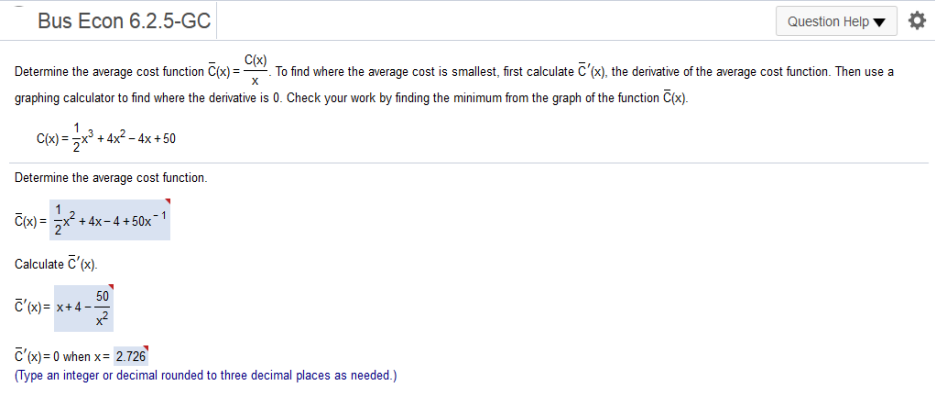
 

 
1/2x³+4x²-4x+50 (divide by x)
 

 
Simplify =
1/2x² + 4x – 4 + 50^-1
Find the derivative     = x + 4 – 50 / x²
x + 4 – 50 / x² = 0,x =   2.72642
  If the pri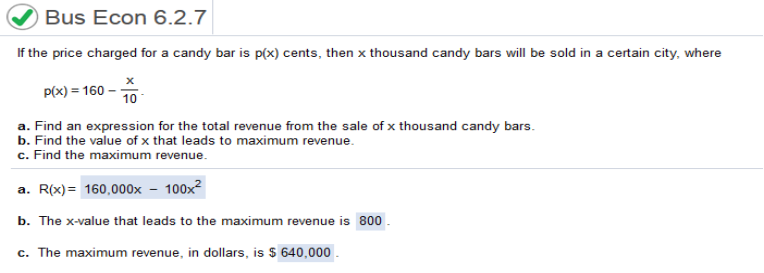ce charged for a candy bar is p(x) cents, then x thousand candy bars will be sold in a certain​ city, where.
p(x) = 160 – x / 10

a.      160 – x / 10 (multiply by 1000 and 100)
160,000x – 100x²
b.      https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/
enter 160,000x – 100x²
Local Maxima – first critical point =
800
c.       Local Maxima – second critical point divided by 100 (drop 2 zeros)
640,000
  A campground owner has 500 m of fencing. He wants to enclose a rectangular field bordering a​ river, with no fencing along the river.​ (See the​ sketch.) Let x represent the width of the field.
​(a) Write an expression for the length of the field as a function of x.
​(b) Find the area of the field (areaequalslength times width) as a function of x.
​(c) Find the value of x leading to the maximum area.
​(d) Find the maximum area.
 

 
a.      500 – 2x
 
b.      (500 – 2x)x
 
c.       (500 – 2x)x
-2x² + 500x | find derivative =
-4x + 500 | solve for zero and x
-4x + 500 = 0 (ti-nspire menu algebra solve)
x = 125 m
 
^d.               -2 x 125(125) = 250(125) = 31,250 m²
  A fence must be built to enclose a rectangular area of 45000 ft².  Fencing material costs $ 3 per foot for the two sides facing north and south and
$6per foot for the other two sides. Find the cost of the least expensive fence.
 

 
2x (3) + 2y(6) =
C = 6x + 12y
xy = 45,000
xy = 45,000 / x
express C in terms of a single variable.
6x + 12(45000 / x)
6x + 540,000/x
 
Enter 6x + 540,000/x
https://www.emathhelp.net/calculators/calculus-1/critical-points-extrema-calculator/
Local Minima
The answer is y (second number
3,600
  A local club is arranging a charter flight to Hawaii. The cost of the trip is $580 each for 82 passengers, with a refund of​ $5 per passenger for each passenger in excess of  82.
a. Find the number of passengers that will maximize the revenue received from the flight.
b. Find the maximum revenue.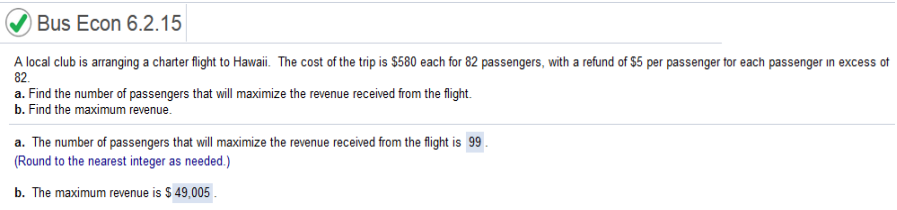
 

a.      580p – 5p(p – 82)
580p – 5p² + 410p (simplify)
-5p² + 990p (find the derivative)
-10p + 990p (solve for zero and x) ti-nspire menu algebra solve
-10p + 990 = 0,p
p = 99
p ≥ 82
 
       b. plug 99 into -5p² + 990p
           -5(99)² + 990(99) = 49,005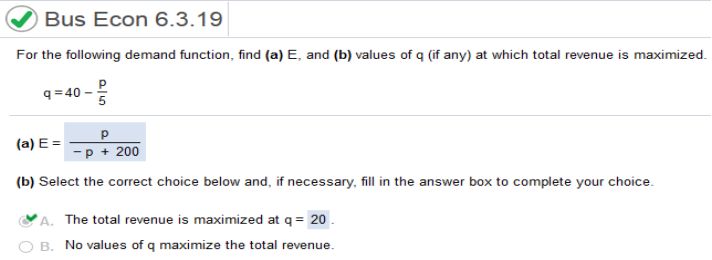
  For the following demand​ function, find ​(a)​ E, and ​(b) values of q​ (if any) at which total revenue is maximized.
 
 

a.      E =
Find derivative for P.
40 – p / 5 =
-1/5
Substitute
     -p
---------------- (-1/5) = p / -p + 200
 
40 – p/5
 
b.
     -p
--------------- (-1/5) = 1
40 – p/5
 
P = 100
40 – (100) / 5 = 20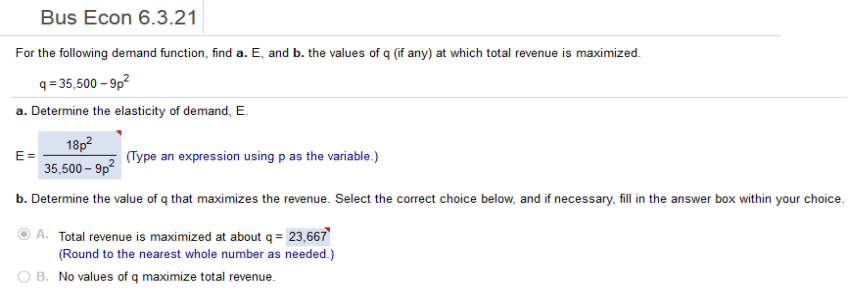
  For the following demand​ function, find a.​ E, and b. the values of q​ (if any) at which total revenue is maximized.
 

Find the derivative.
35,500 – 9p² = -18p
 
              p
  - -----------------------   (-18p) =
      35,500 – 9p²
 
18p² / -9p² + 35,500
 
1 = 18p² / -9p² + 35,500 (Multiply both sides by the denominator)
35500 – 9p² = 18p² (collect p terms)
35500 = 27p² (divide by 27)
P² = 1314.814815
Plug p² in and round.
35,500 – 9(1314.814815)
23,667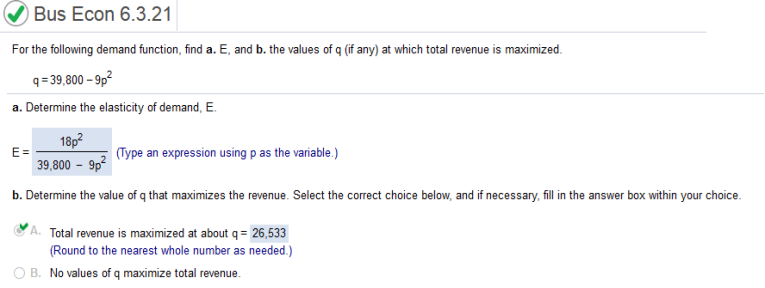
 
   
For the following demand​ function, find a. ​E, and b. the values of q​ (if any) at which total revenue is maximized.
 
p = 300_e^-0.5q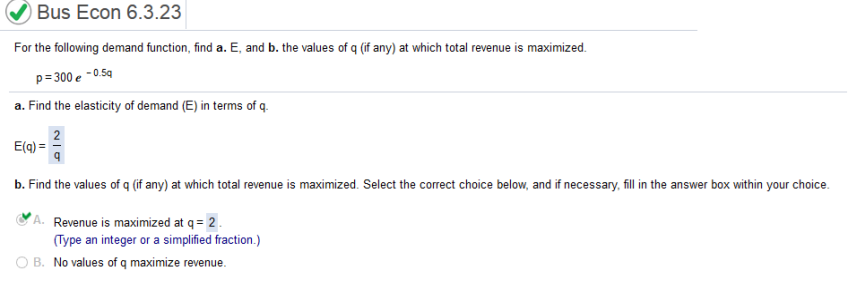
 

a.
Derivative       -p / 403 - .2p² (-.4p)                .4p² / 403 - .2p²
 
q(-300 e^-0.5q)
-----------------------                 Find d/dq = 2 then divide by q
    150 e^-.5q
 
 b.
plug in 1 for q.
2 / 1 = 2
   
The​ short-term demand for crude oil in Country A in 2008 can be approximated by q = f(p) = 2,154003p^-0.07 where p
represents the price of crude oil in dollars per barrel and q represents the per capita consumption of crude oil.
Calculate and interpret the elasticity of demand when the price is $97 per barrel.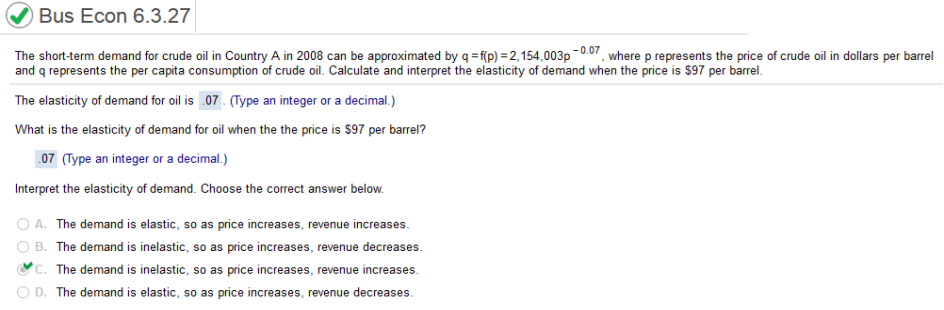
 

Find the derivative.
2154003p^-.07 (can multiply the coefficient by the exponent and subtract one from the exponent)
-150780.21p^-1.07 (be sure to move the derivative down to see the entire number)
P / 2154003p^-.07(-150780p^-1.07)
-150780.21p^-.07 / 2154003p^-.07 (Simply by cancelling the common variable and dividing)
150780.21 / 2154003 =          0.07
   
A software entertainment company recently ran a holiday sale on its popular software program. Using data collected from the​ sale,
it is possible to estimate the demand corresponding to various discounts in the price of the software. Assuming that the original price was
​$40, the demand for the software can be estimated by the function q equals 3 comma 471 comma 000 p Superscript negative ^2.131, where p
is the price and q is the demand. Calculate and interpret the elasticity of demand.
 
The elasticity of demand is the exponent but Positive.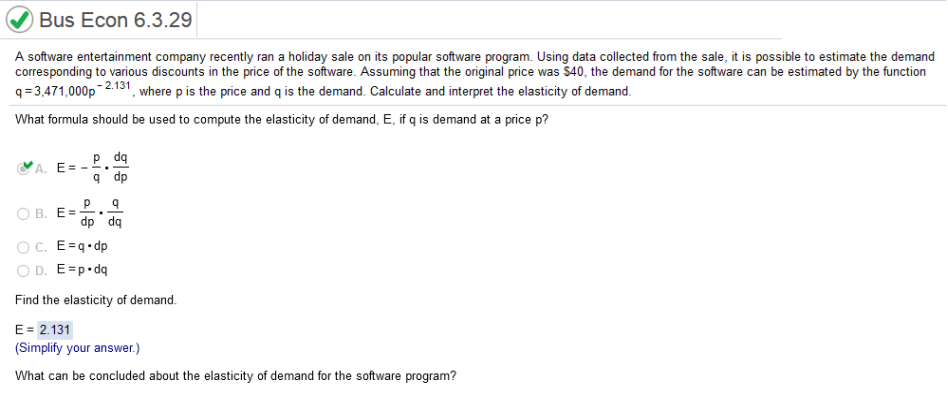
 


The answers are given
   
A study of the demand for air travel between two cities depends on the airfare according to the following demand equation.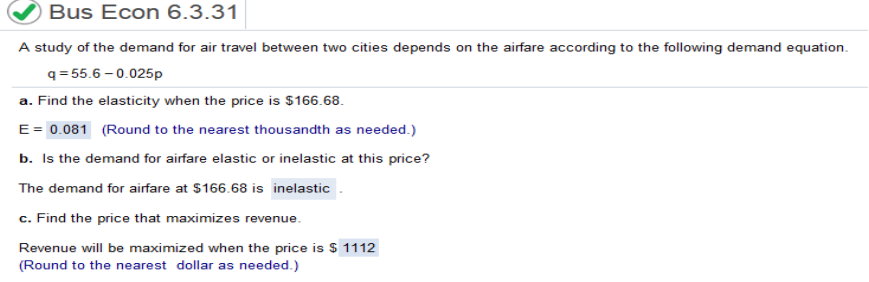
 

 
55.56 - .025p (the derivative times -p divided by the function)
-p(-.025) / 55.6 - .025p =
.025p / 55.6 - .025p
Plug in 166.68 for p.
.025(166.68) / 55.6 - .025(166.68) = .081
 
Revenue will be maximized when the price is ___ ​(Round to the nearest  dollar as​ needed.)

solve    0.025p / 55.6 - 0.025p = 1     =     1112
   
Watch the Marginal Analysis and Approximation video and then answer the question given below.
In the​ video, what calculation is given that would estimate the cost of producing the third shirt at Greko​ Graphics?
 
 
Homework: Section 6.5 Assume x and y are functions of t. Evaluate dy/dt for the following
y³ = 2x⁴ + 32; dx/dt = 5, x = 2, y = 4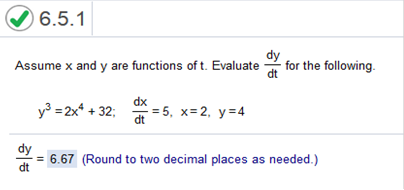
 

Find derivative.
y³ = 2x⁴ + 32
3y² = 8x³
plug in values of x = 2, y = 4, dx/dt = 5 (dx/dt is multiplied on the right side)
3(4)² = 8(2)³(5)
48 = 320
320 / 48 = 6.66667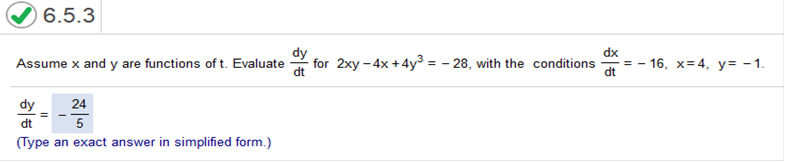
  Assume x and y are functions of t. Evaluate For with the conditions

 
Solve the equation for dy/dx.
Plug in the values of x and y. x = 4, y = -1
Then multiply by the value of dx/dt (-16)
A manufacturer of handcrafted wine racks has determined that the cost to produce x units per month is given by C = 0.2x² + 7,000.
How fast is the cost per month changing when production is changing at the rate of 17 units per month and the production level is 80 units?

Find the derivative of 0.2x² + 7,000.
.4x
.4(17 x 80) = 544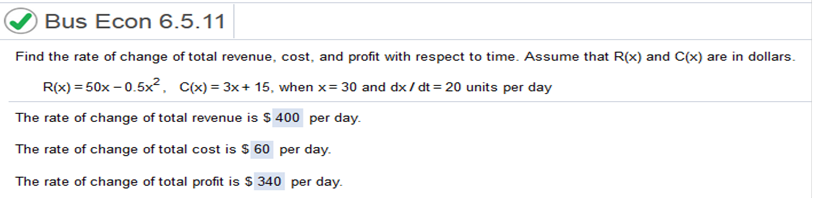
  Find the rate of change of total​ revenue, cost, and profit with respect to time. Assume that​ R(x) and​ C(x) are in dollars.


Find the derivative of 50x - .5x² = 50 – x
plugin the value of X and multiply by dx/dt.
50(20) – (30)(20) =      400
Find the derivative of 3x + 15
then multiply it by the value of dx/dt
3(20) =                         60
Subtract 400 by 60 = 340
   
The demand function for a certain product is determined by the fact that the product of the price and the quantity demanded
equals 6000.  The product currently sells for $2.20 per unit. Suppose manufacturing costs are increasing over time at a rate of 16% and
the company plans to increase the price p at this rate as well. Find the rate of change of demand over time. Find the demand function
represented in this problem where p is the price of the product and q is the quantity demanded for the product.
 

-6,000 ÷ 2.20² x .16 x 2.20 = -436.36363… (round to 436)
The answer is negative, however, it is decreasing at a rate of POSITIVE 436 units per unit of time.
   
Sociologists have found that crime rates are influenced by temperature. In a town of 200,000 people, the crime rate has been approximated as
C = 1/10(T – 60)² where C is the number of crimes per month and T is the average monthly temperature in degrees Fahrenheit. The average
temperature for May was 72 degrees and by the end of May the temperature was rising at the rate of 5 degrees per month. How fast is the
crime rate rising at the end of​ May?

 
Find the derivative of 1/10(T – 60)² (d/dt)
plugin in the value of T with (72)
then multiply it by (5)
   
An 18-foot ladder is leaning against a building. If the bottom of the ladder is sliding along the pavement directly away from the building at
1 feet/second, how fast is the top of the ladder moving down when the foot of the ladder is 4 feet from the​ wall.
 

 
I wrote this formula, and it works…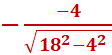
(1) = 0.22792115 (round to 0.228)
   
A rock is thrown into a still pond. The circular ripples move outward from the point of impact of the rock so
that the radius of the circle formed by a ripple increases at the rate of 5 feet per minute. Find the rate at which
the area is changing at the instant the radius is 16 feet.
 

 
(2π)5 x 16 = 502.65482457 (round to 502.655)

---

---