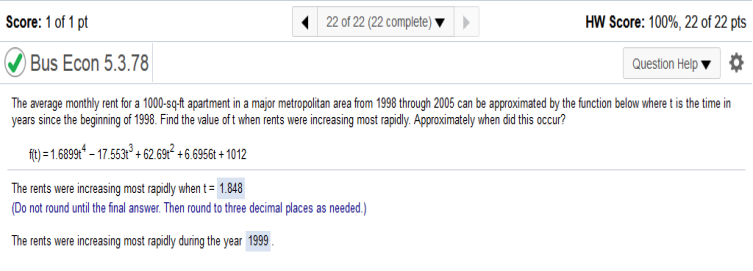
|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Homework Chapter
1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM Need A Tutor? Need Homework Help?
Calculus For Business Homework Chapter 4 Part B Use the derivative to find the vertex of the parabola. y = -x2 + 4x + 2 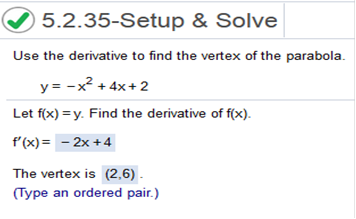
Explanation 1st Part We need to find the derivative of -x2 + 4x + 2 n-1 -x2 = -2x n-1 4x = 4 n-1 2 = 0 The answer is -2x + 4 Explanation 2nd Part We need to solve -2x + 4 = 0 First, we subtract 4 from both sides -2x + 4 = 0 = -2x = -4 Now we divide -4 / -2 = 2 Now we plug 2 into -x2 + 4x + 2 -(2)2 + 4(2) + 2 = -(4) + 8 + 2 = -4 + 8 + 2 = 4 + 2 = 6 For the cost and price functions below, find a) the number, q, of units that produces maximum profit; b) the price, p, per unit that produces maximum profit; and c) the maximum profit, P. C(q) = 80 + 15q, p = 67-2q 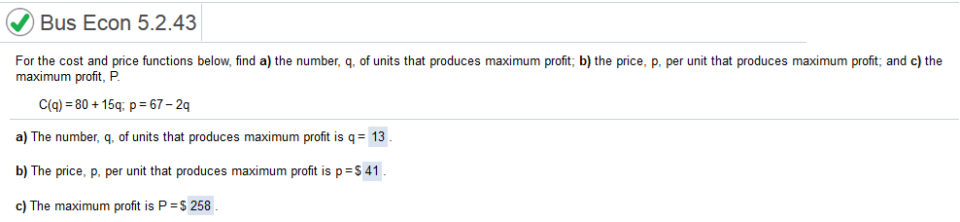
First part q (67 – 2q) = -2q2 + 67q Now we subtract C(q) = 80 + 15q and simplify. -2q2 + 67q – 80 – 15q = -2q2 + 52q – 80 Now we find the derivative of -2q2 52q – 80 n-1 (-2q2 + 52q – 80) = -4x + 52 Now we set equal to 0 and solve -4q + 52 = 0 add 4q to both sides = 52 = 4q Now we divide both sides by 4 = q = 13 Second part Nex we Plug 13 into p = 67 – 2q 67 – 2(13) = 41 Third part We subtract -2q2 + 67q – 80 - 15q = -2q2 + 52q – 80 Next, we plug in 13 into -2q2 + 52q – 80 -2(13)2 + 52(13) – 80 = 258 For the cost and price functions below, find the number, q, of units that produces maximum profit; b) the price, p, per unit that produces maximum profit; and c) the maximum profit, P. C(q) = 80 + 18q; p = 66 - 2q 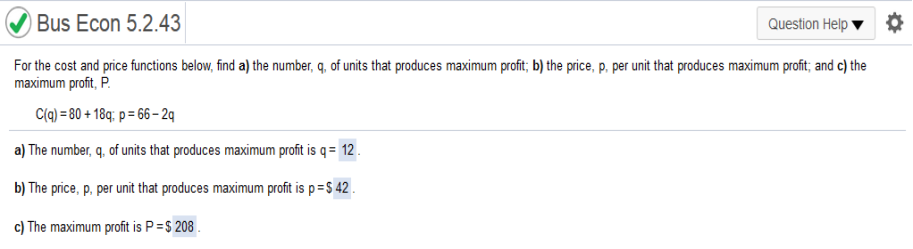
q(66 – 2q) = -2q2 + 66q -2q2 +66q – 18q – 80 = -2q2 + 48q – 80 Find derivative = -4q + 48 and solve for q The number, q, of units that produces maximum profit is q = 12 66 – 2(12) = 42 The price, p, per unit that produces maximum profit is p = $42 -2q2 + 48q – 80 -2(12)2 + 48(12) – 80 = c) The maximum profit is P = $208 For the cost and price functions below, find (a) the number, q, of units that produces maximum profit; (b) the price, p, in dollars per unit that produces maximum profit; and (c) the maximum profit, P, in dollars. 
Explanation q(80e-.05) = 80q e-.05 80q e-.05q – 40 + 20q e-.05q = 60q e-.05q – 40 60q e.05q – 40 - qe.05q = 60 – 40 = 20 e = 2.71828 80(2.71828) -.05(20) 29.4304 = 29.43 60 (20) (2.71828) -.05(20) – 40 = 401.456 = Answer: 401.46 The total profit P(x) (in thousands of dollars) from a sale of x thousand units of a new product is given by ln (-x3 + 3x2 + 144x + 1) (0 ≤ x ≤ 10) a) find the number of units that should be sold in order to maximize the total profit. b) What is the maximum profit? 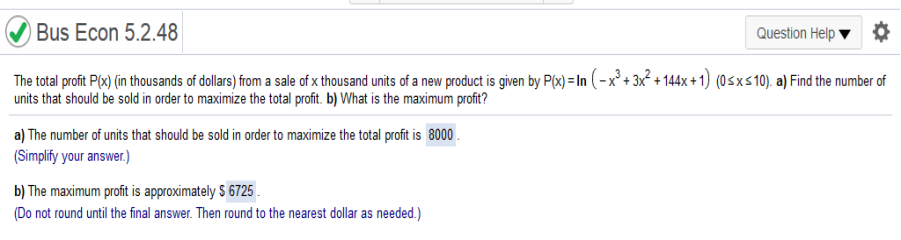
Find the derivative of ln (-x3 + 3x2 + 144x + 1) -3x2 + 6x + 144 / -x3 + 3x2 + 144x + 1 = 0 Use only the positive number 8 and multiply by one thousand = 8000 Suppose that the cost function for a product is given by C(x) = 0.002x3 + 7x + 6406 Find the production level (that is, the value of x) that will produce the minimum average cost per unit C(x) 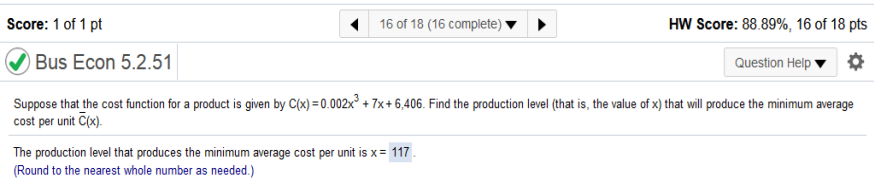
The production level that produces the minimum average cost per unit is Divide and simplify .002x3 + 7x + 6406 = .002x2 + 7 + 6406 / x Find derivative of .002x2 + 7 + 6406 / x = .004x – 6406 / x2 Solve for x for zero (menu algebra solve) Enter .004x – 6406 / x2 = 0,x 116.999 = 117 After a great deal of experimentation, two college senior physics majors determined that when a bottle of French champagne is shaken several times, held upright, and uncorked, its cork travels according to the function below, where s is its height (in feet) above the ground t seconds after being released. 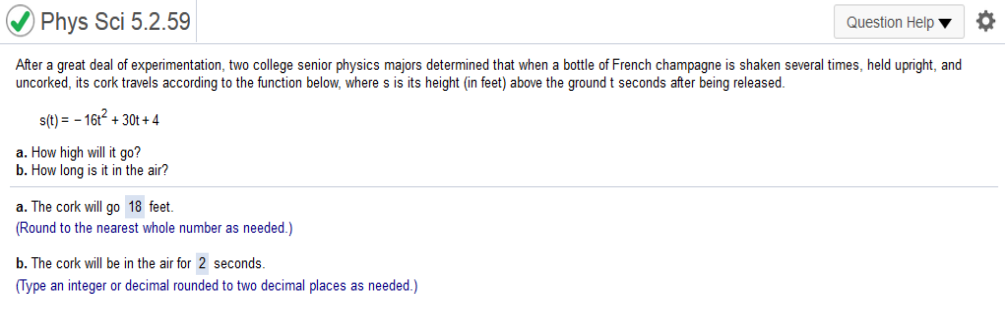
a. Find derivative of -16t2 + 30t + 4 = -32t + 30 Solve for zero/t = 15/16 = menu number to decimal = 0.9375 Plug into the equation -16(.9375)2 + 30(.9375) + 4 = 18.0625 = 18 b. we need to solve the quadratic equation -16t2 + 30t + 4 = 0. a = -162, b = 30, and c = 4 Check the Critical Points box. What do the critical points correspond to? (Use the interactive figure to find your answer.) Click here to launch the interactive figure. 
A. The critical points correspond to the zeros of f’(x) B. The critical points correspond to the y-intercept. C. The critical points correspond to where the derivative is the greatest. Find the open intervals where the function is concave upward or concave downward. Find any inflection points. 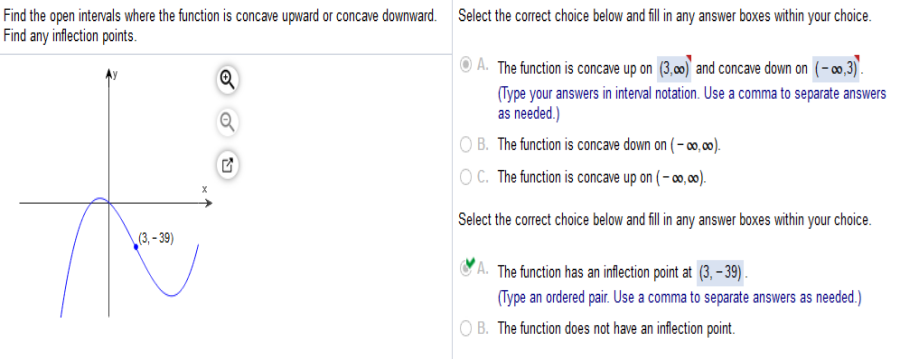
Study the graph 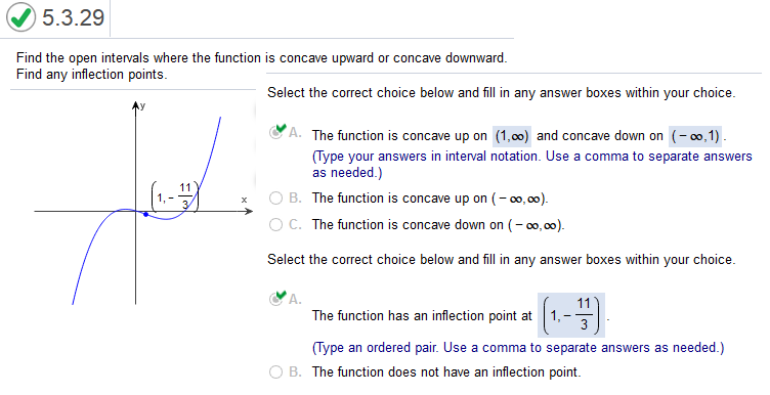
Study the graph 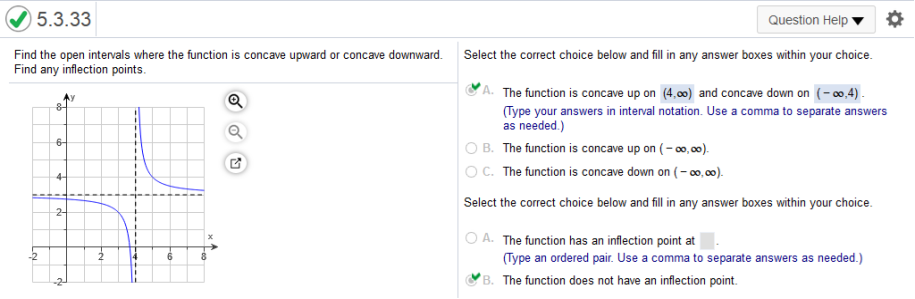
Study the graph Find the open intervals where the function is concave upward or concave downward. Find any inflection points. f(x) = 3x2 + 11x - 5 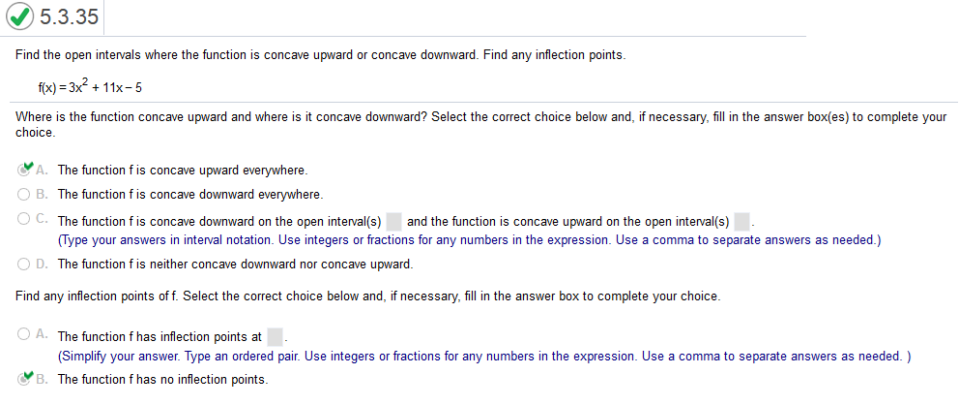
Find the second derivative. 1st derivative = 6x + 11 = 2nd derivative = 6 The second derivative is positive, so the function f is concave upward and there are no infectious points. Find the open intervals where the function is concave upward or concave downward. Find any inflection points. f(x) = -2x2 – 2x + 2 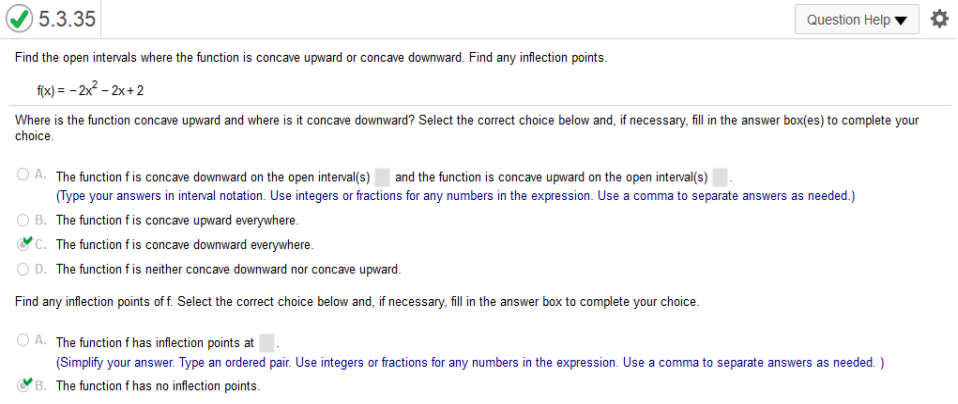
Find the second derivative = -2 Since it is negative, function f is downward everywhere https://www.emathhelp.net/calculators/calculus-1/function-calculator/ -2x^2–2x+2 enter equation then look at Concave upward on Concave downward on Concave down if -∞, ∞ Then look at Inflection Points Find the open intervals where the function f(x) = 
Find the open intervals where the function f(x) = -2x3 + 12x2 +169x -9 is concave upward or concave downward. Find any inflection points. https://www.emathhelp.net/calculators/calculus-1/function-calculator/ enter equation 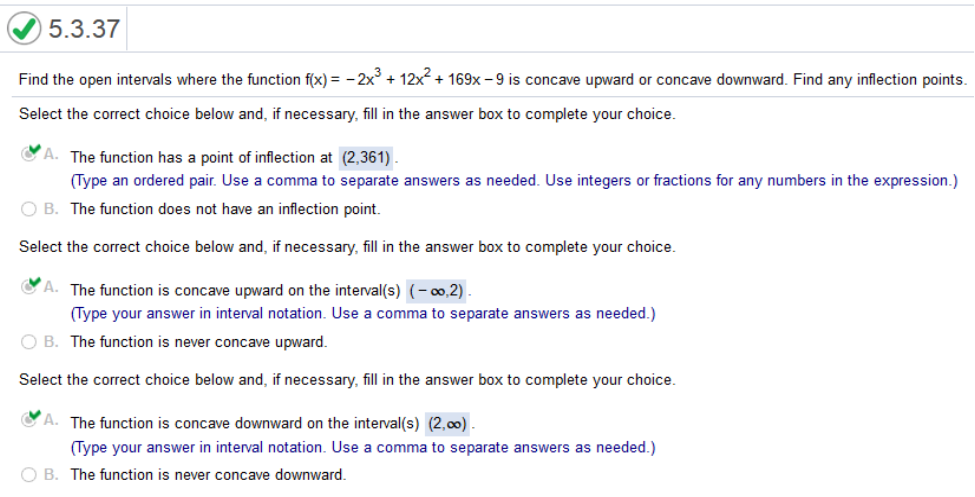
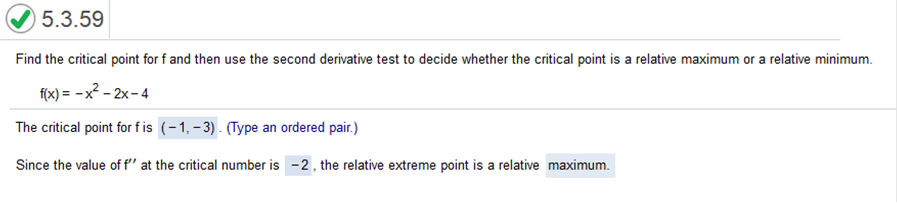
Find the critical point for f and then use the second derivative test to decide whether the critical point is a relative maximum or a relative minimum. Find the derivative Then solve for zero and x Then plug the value into the original equation Value of x and the answer are the critical points Then follow the second derivative test. The second derivative is -2 The second derivative test states the following. 
numbers lead to relative maxima or relative minima. If the second derivative test gives no information, use the first derivative test instead. https://www.emathhelp.net/calculators/calculus-1/function-calculator/ find derivative first then enter the equation and go to x-intercepts use the bottom maximum at smallest, minimum at largest 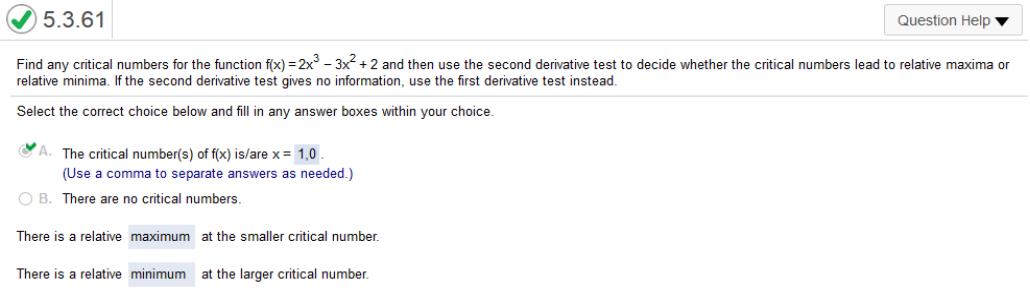

https://www.emathhelp.net/calculators/calculus-1/function-calculator/ 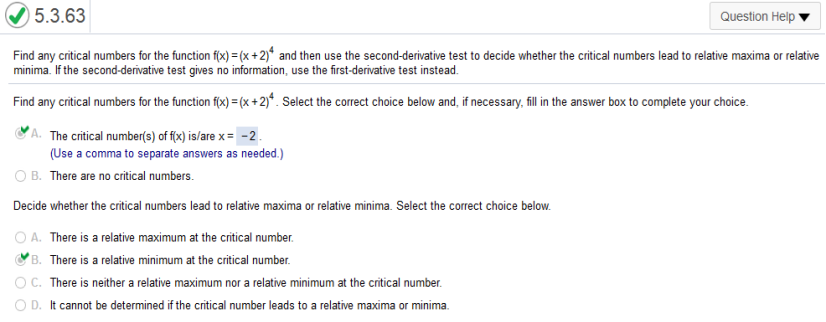
Find second derivative then go to menu algebra solve for zero and x. then plug the answer into the equation 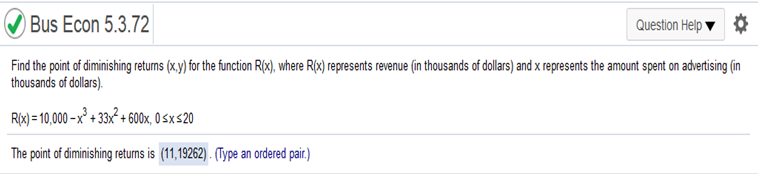
For the function f(x) = 3x3 -8x2 + 13x + 4. find f”(x) then find f”(0) and f”(3) f”(x) means derivative. Find the second derivative and plug in the values (0) and (3) 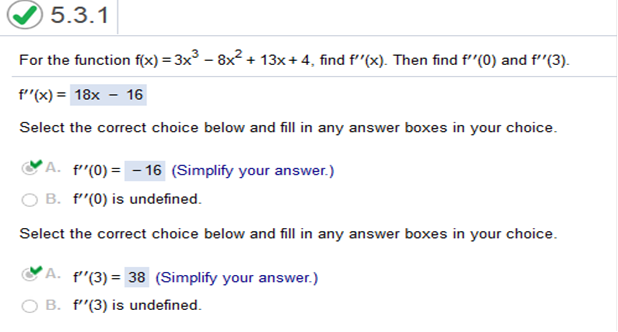
For the function f(x) = x2 / 2 + x find f”(x) then find f”(0) and f”(3) 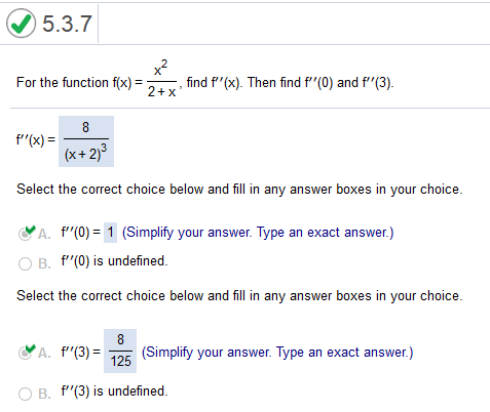
Find the second derivative Then solve the quadratic equation. Plug both solutions in and use the largest of the two. Then add on to the year
inflection points, regions where the function is concave upward or concave downward, intercepts where possible, and asymptotes where applicable. First find first and second derivatives. Then go to https://www.emathhelp.net/calculators/calculus-1/function-calculator/ enter the function and use the local minima and maxima. Local Minima (−4,−844) Local Maxima (3,528) 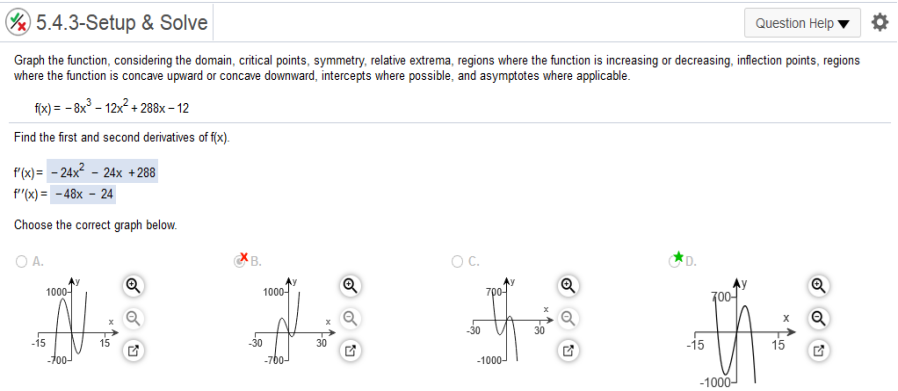
Local Minima (−5,−289) Local Maxima (2,54) 
regions where the function is concave upward or concave downward, intercepts where possible, and asymptotes where applicable. https://www.emathhelp.net/calculators/calculus-1/function-calculator/ enter the function and use the local minima and maxima. Local Minima (−4,−636) Local Maxima (3,393) 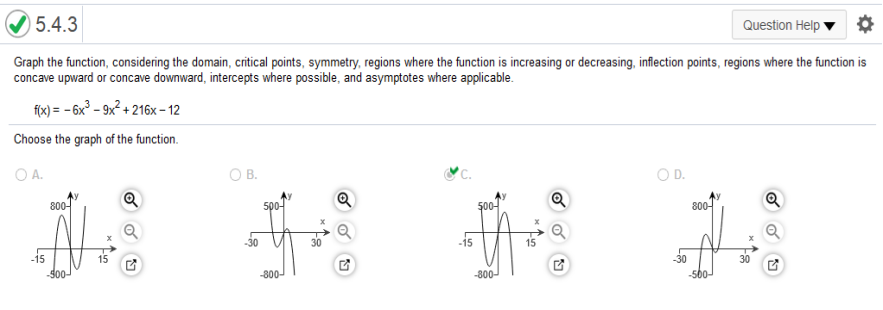

regions where the function is concave upward or concave downward, intercepts where possible, and asymptotes where applicable. https://www.emathhelp.net/calculators/calculus-1/function-calculator/ enter the function and use the local minima and maxima. Local Minima (0,−2812) Local Maxima No maxima. 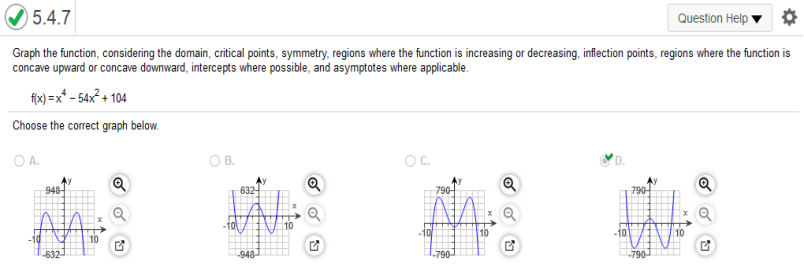
Local Minima (0,−2587) Local Maxima No maxima. 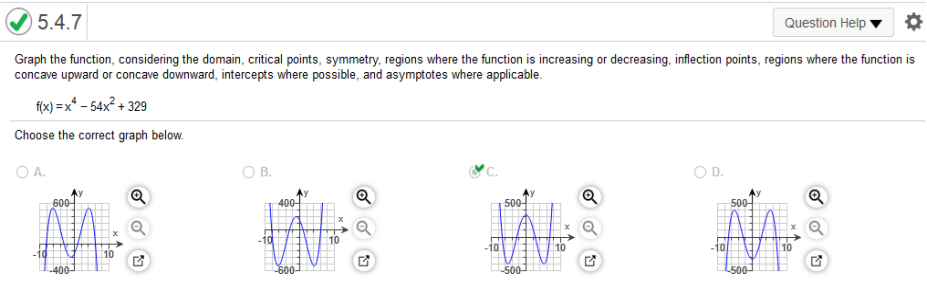
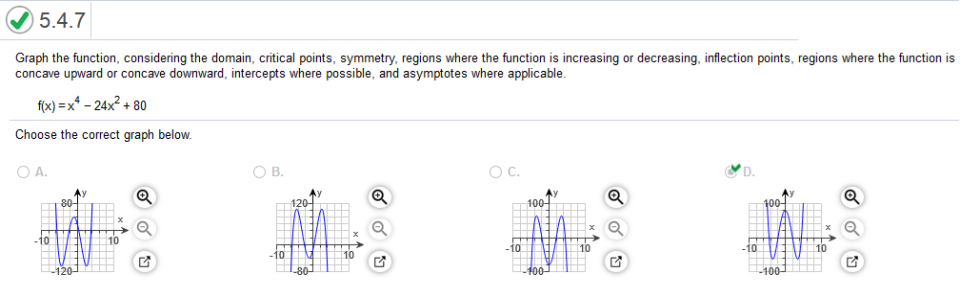
regions where the function is concave upward or concave downward, intercepts where possible, and asymptotes where applicable. https://www.emathhelp.net/calculators/calculus-1/function-calculator/ enter the function and use the local minima and maxima. Local Minima (0,−2812) Local Maxima No maxima. 


inflection points, regions where the function is concave upward or concave downward, intercepts where possible, and asymptotes where applicable. Find the first and second derivatives with the ti-nspire. Then go to https://www.emathhelp.net/calculators/calculus-1/function-calculator/ enter the function and go to the bottom. Graph For graph, see graphing calculator. 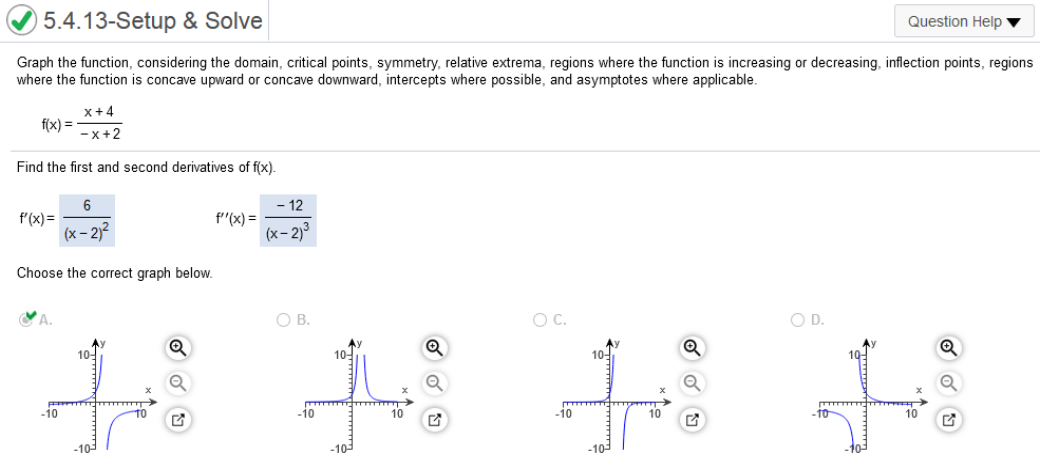
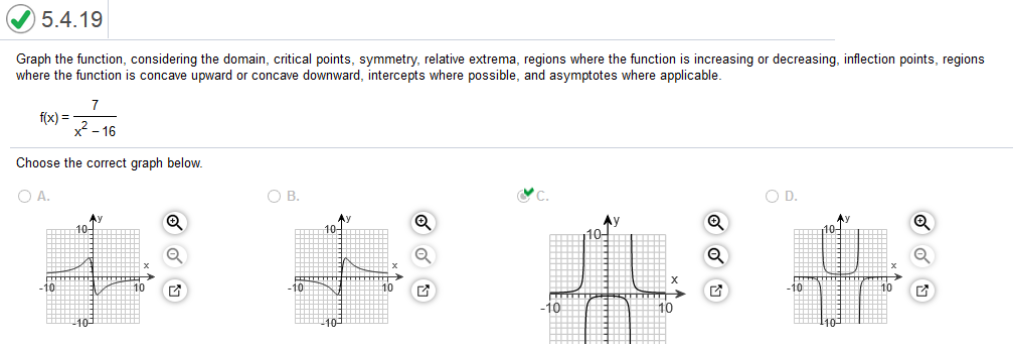
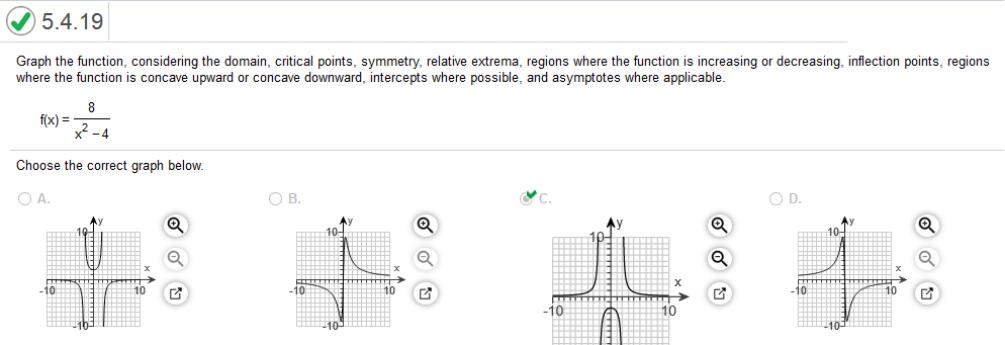
The graph of a company's profit P(t) in dollars, at month t is shown. Complete parts a through e below. 

Study the graph Complete parts a and b below. 

Study the graph The graph of a company’s profit P(t) in dollars, at month t is shown Complete parts a through e below 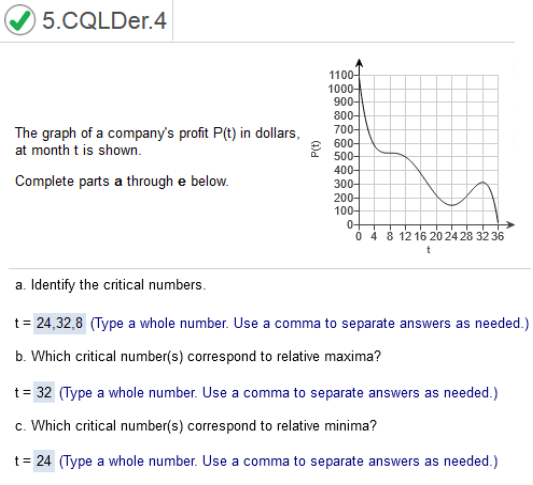

Study the graph The graph of a company's profit P(t) in dollars, at month t is shown. Complete parts a and b below. 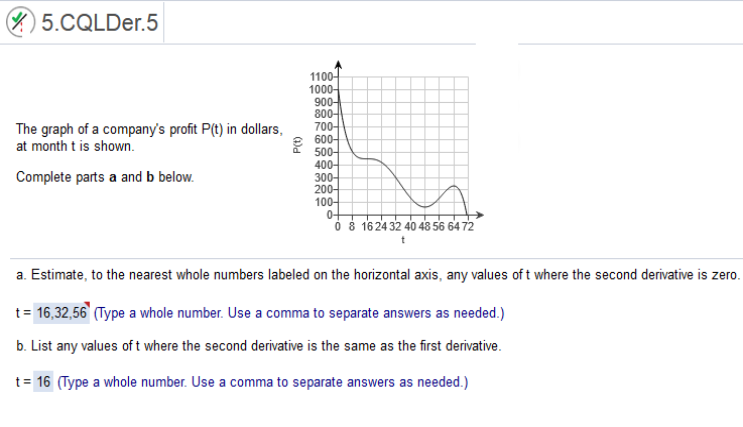
Study the graph The graph of a company's profit P(t) in dollars, at month t is shown. Complete parts a and b below. 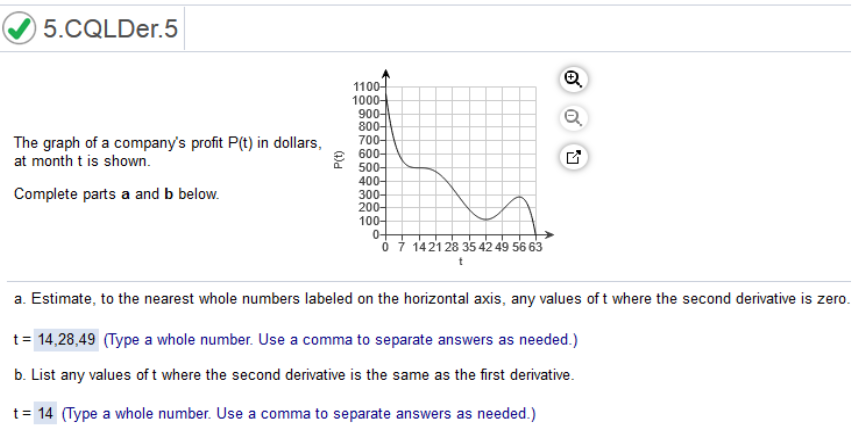
Study the graph The graph of a company's profit P(t) in dollars, at month t is shown. Complete parts a and b below. 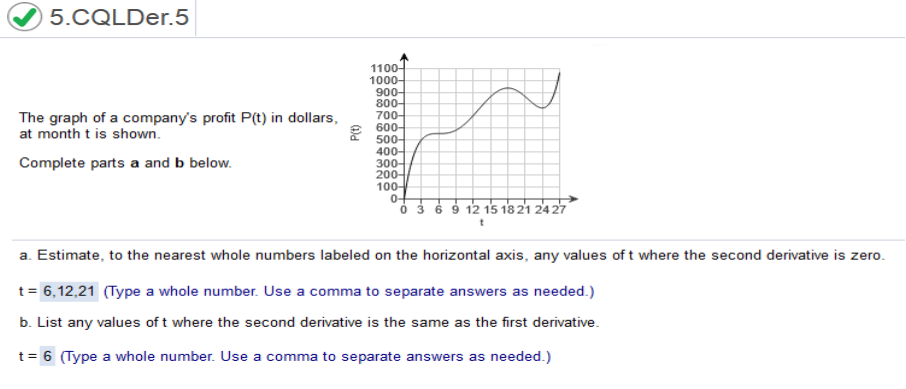
Study the graph The daily demand, q, for cupcakes is a function of the price p, where q = f(p) = 150 – 39p 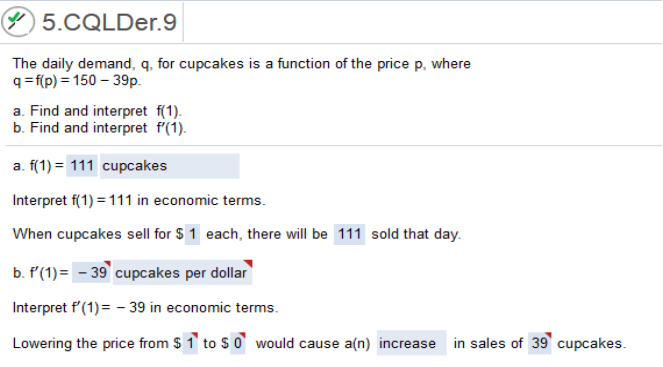
a. plug in the value of f(p) = 1 f(p) = 150 – 39(1) = 111 b. we need to find the derivative and then plug in the value of f’(1) *f’ = derivative f’ = 150 – 39p = -39(1) = 39 The daily demand, q, for cupcakes is a function of the price p, where q = f(p) = 110 – 28p 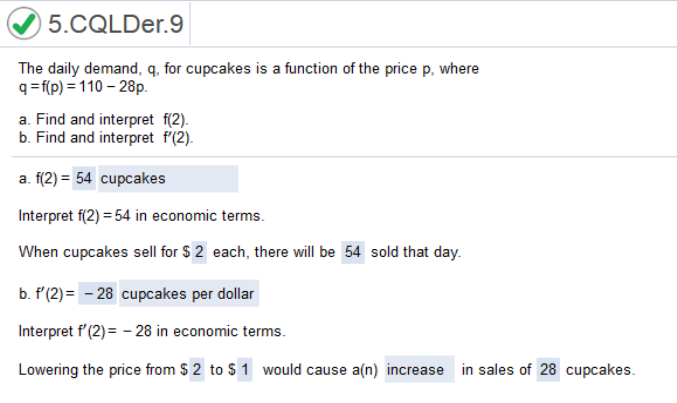
a. plug in the value of f(p) = 2 f(p) = 110 – 28(2) = 54 b. we need to find the derivative and then plug in the value of f’(2) *f’ = derivative f’ = 110 – 28p = -28(2) = 28 Homework Chapter
1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM Need A Tutor? Need Homework Help?
|
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |