|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Homework Chapter
1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM Need A Tutor? Need Homework Help?
Calculus For Business Homework Chapter 4 Part A 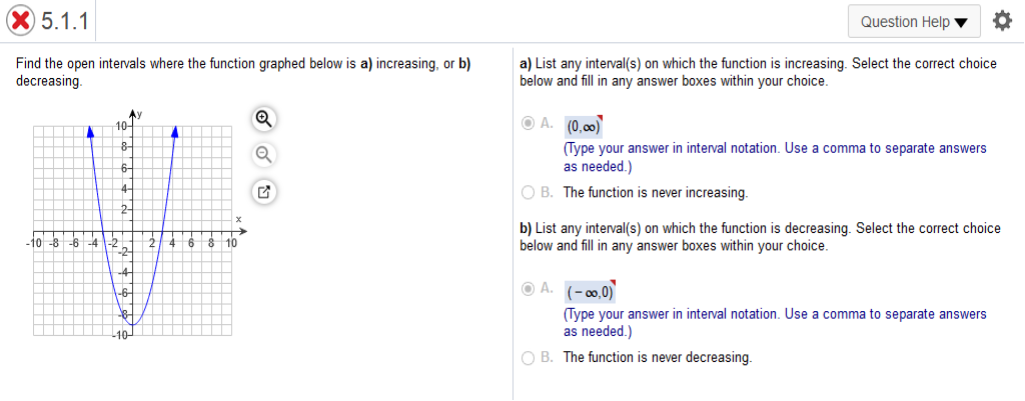
Study the graph. You can see the curve at 0 and increasing indefinitely and vice versa. 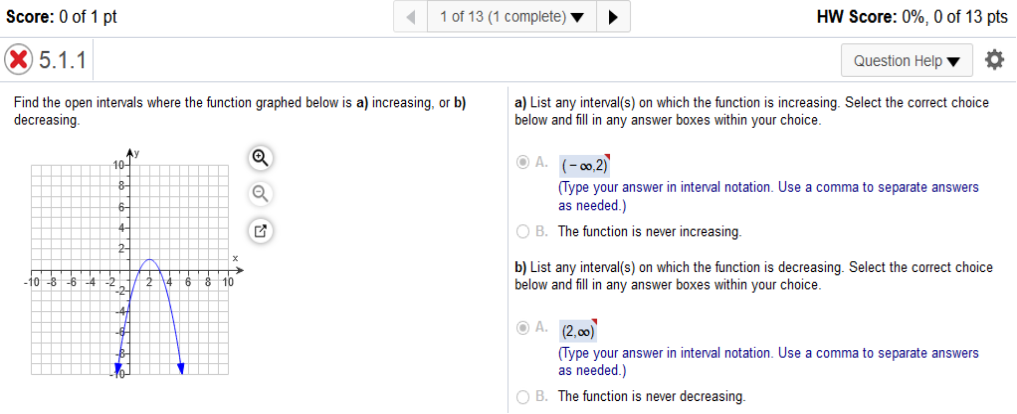
Same here. Study the graph. You can see the curve at positive 2 and increasing indefinitely and vice versa. 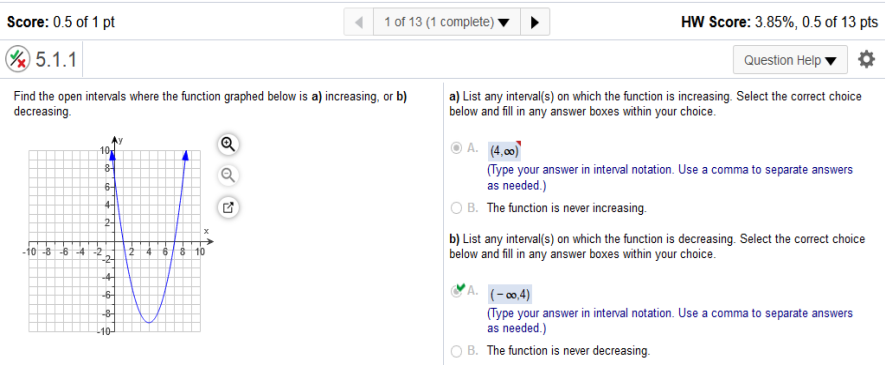
Same here. Study the graph 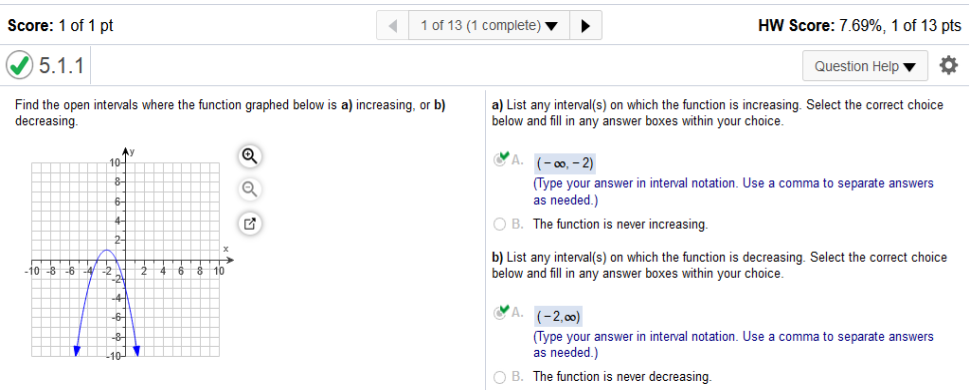
Same here. Study the graph Find the open intervals where the function graphed below is a) increasing, or b) decreasing. 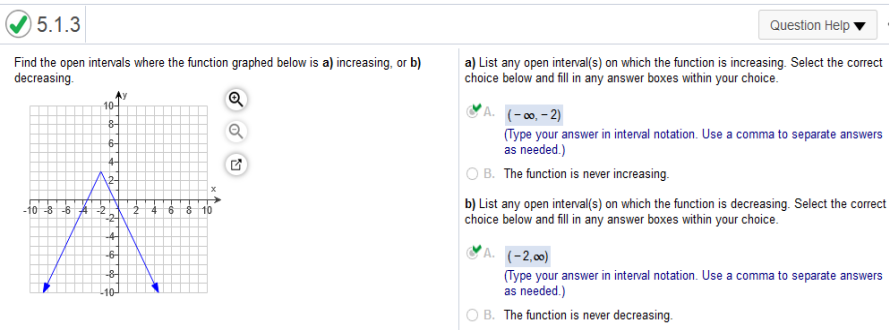
Same here. Study the graph 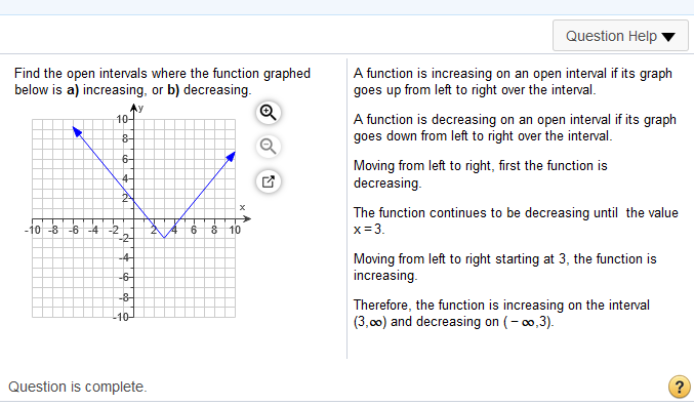
Same here. Study the graph Find the open intervals where the function graphed below is a) increasing, or b) decreasing. 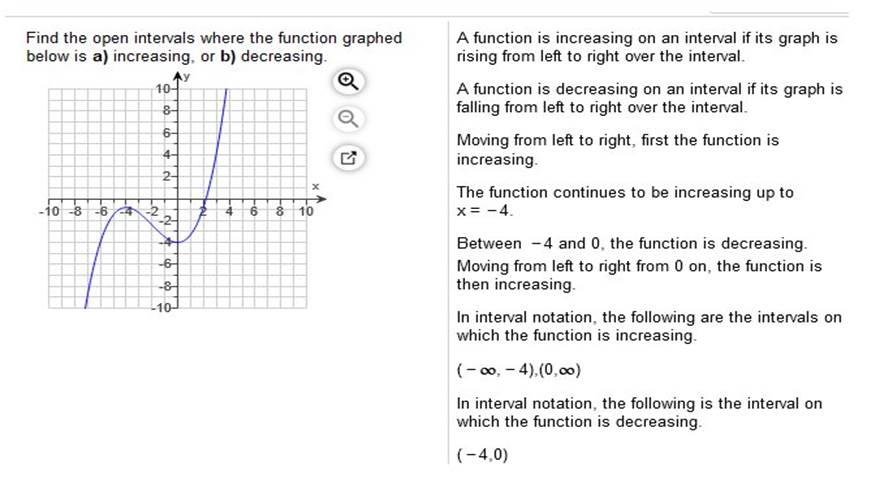
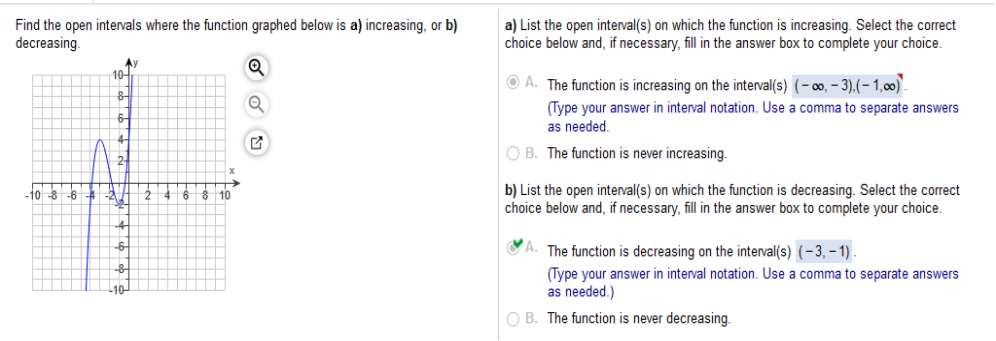
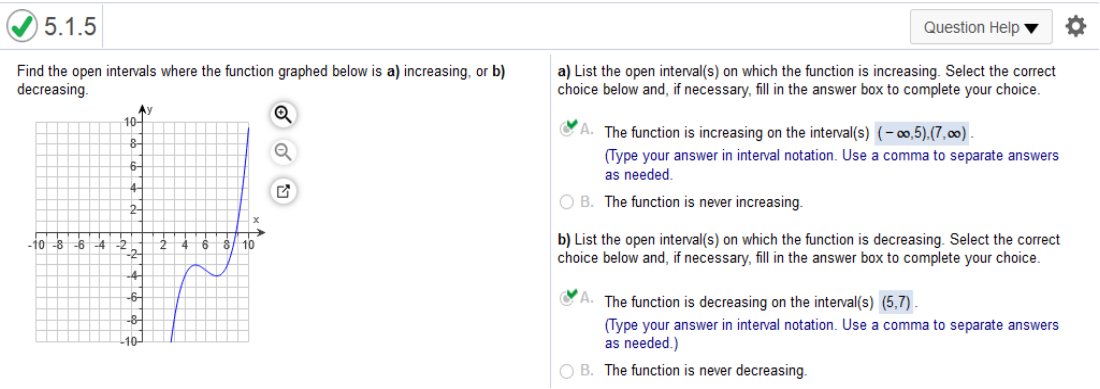
Find the open intervals where the function graphed below is (a) increasing, or (b) decreasing. 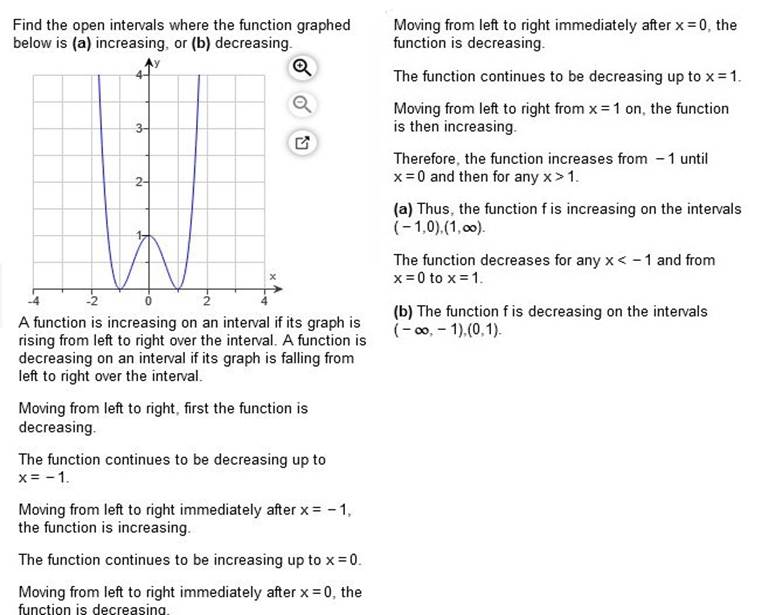
Study the graph and answers! Find the open intervals where the function graphed below is a) increasing, or b) decreasing. 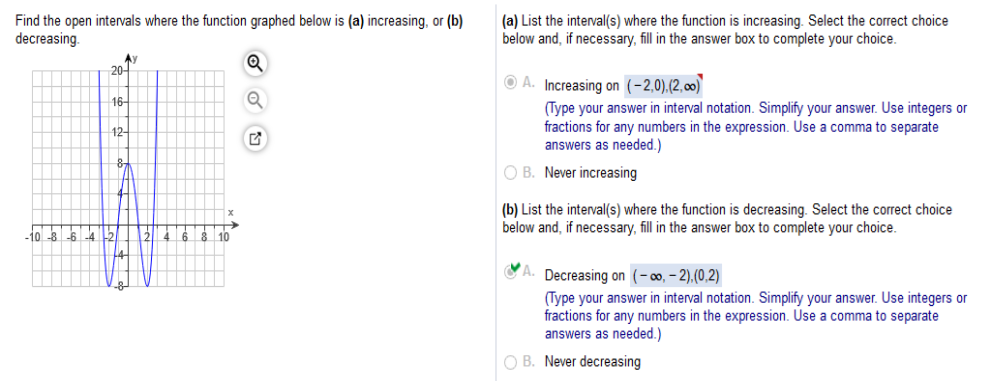
Study the graph and answers! 
Study the graph and answers! Find the locations and values of all relative extrema for the function with the graph below. 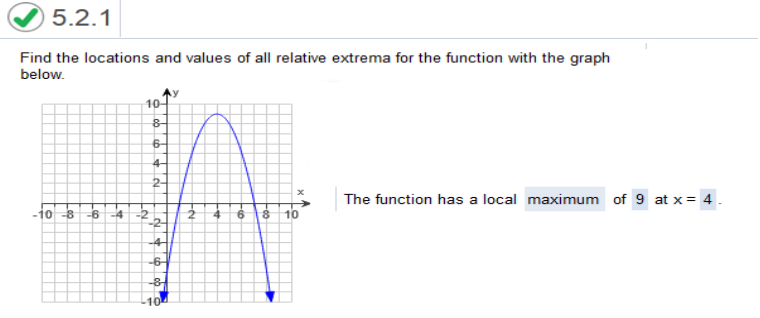
Study the graph and answers! Find the locations and values of all relative extrema for the function with the graph below. 
Study the graph and answers! For the function below, find (a) the critical numbers; (b) the open intervals where the function is increasing; and (c) the open intervals where it is decreasing. f(x) = 2.7 + 3.4x – 0.7x2 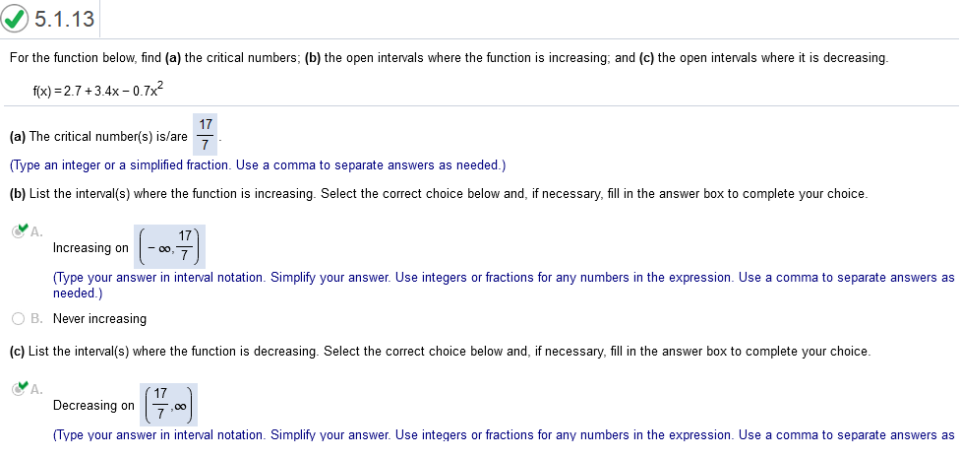
2.7 + 3.4x – 0.7x2 -1.4x + 3.4 -1.4x + 3.4 = 0 -1.4x = -3.4 x = 3.4/1.4 Check https://www.emathhelp.net/calculators/calculus-1/function-calculator 2.7 + 3.4x – 0.7x2 For the function below, find (a) the critical numbers; (b) the open intervals where the function is increasing; and (c) the open intervals where it is decreasing. 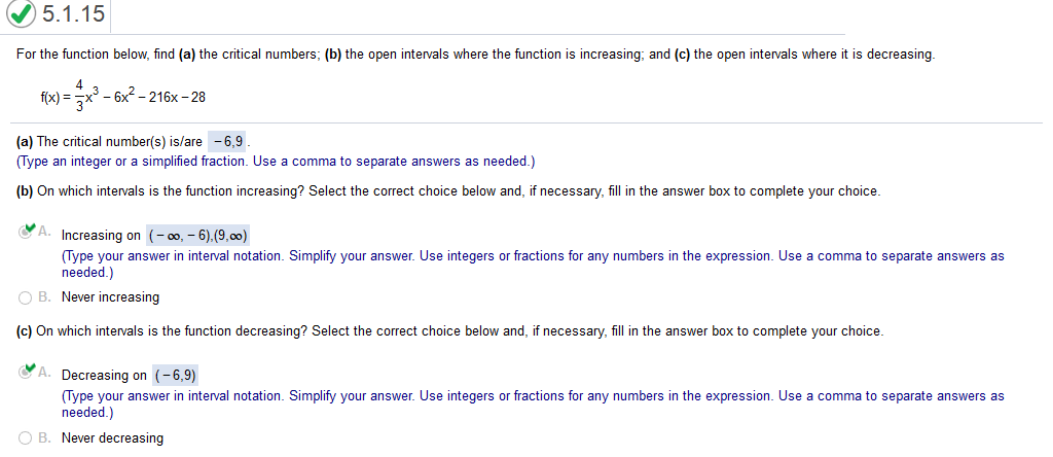
a. explanation Find the derivative of You should know how to find the derivative of a function by now. So, the derivative of Now we set the derivative to equal zero 4x2 – 12x – 216 = 0 https://quickmath.com/ 4x2 – 12x – 216 = 0 x = -6, 9 So, the critical numbers are -6, 9 Check https://www.emathhelp.net/en/calculators/calculus-1/critical-points-extrema-calculator/ For the function below, find a) the critical numbers; b) the open intervals where the function is increasing; and c) the open intervals where it is decreasing. f(x) = 8x3 – 42x2 – 360x + 4 
Find the derivative of 8x3 – 42x2 – 360x + 4 = 24x2 – 84x Set = 0 24x2 – 84x -360 = 0 https://quickmath.com/ The critical Numbers are 6, -5/2 Check https://www.emathhelp.net/calculators/calculus-1/function-calculator/ 8x3 – 42x2 – 360x+4 For the function below, find (a) the critical numbers; (b) the open intervals where the function is increasing; and (c) the open intervals where it is decreasing. f(x) = 2.5 + 2.2x – 0.6x2 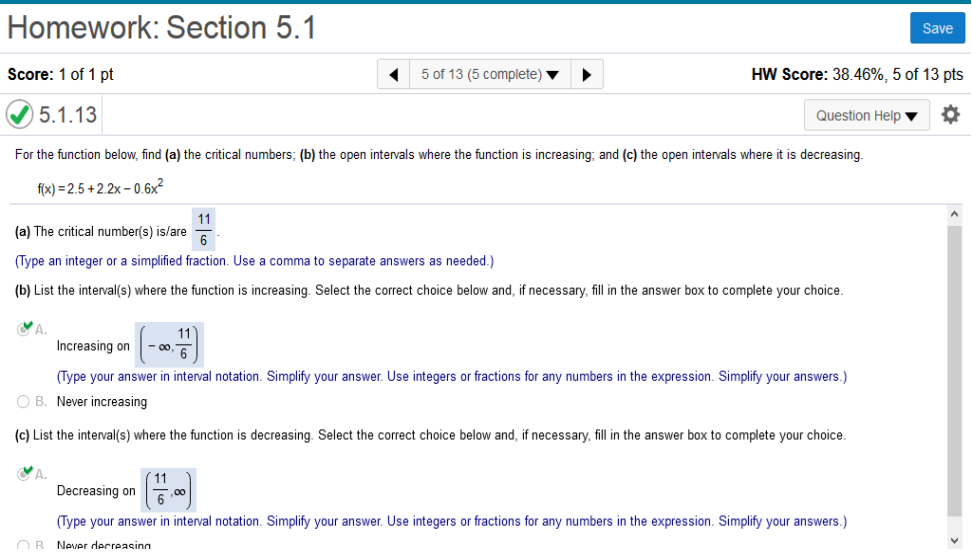
Find the derivative of 2.5 + 2.2x – 0.6x2 = https://www.emathhelp.net/calculators/calculus-1/function-calculator For the function below, find (a) the critical numbers; (b) the open intervals where the function is increasing; and (c) the open intervals where it is decreasing 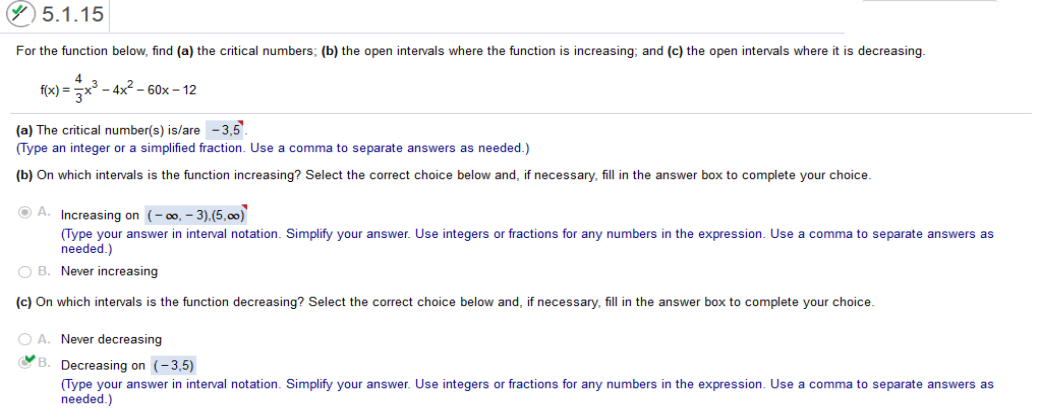
https://www.emathhelp.net/calculators/calculus-1/function-calculator a. Critical points are the values of x and x. b. Intervals of Increase as stated in results c. Decreasing - Intervals of Decrease as stated For the function below, find (a) the critical numbers; (b) the open intervals where the function is increasing; and (c) the open intervals where it is decreasing. https://www.emathhelp.net/calculators/calculus-1/function-calculator a = 2nd and first numbers of Intervals of Increase b = Intervals of Increase (common (),() ) c = Intervals of Decrease 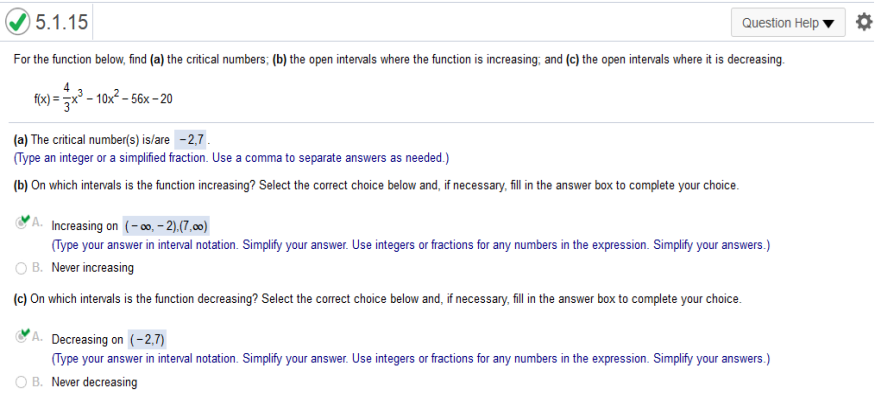
For the following function, find a) the critical numbers, b) the open intervals where the function is increasing, and c) the open intervals where it is decreasing. y = -3x - 10 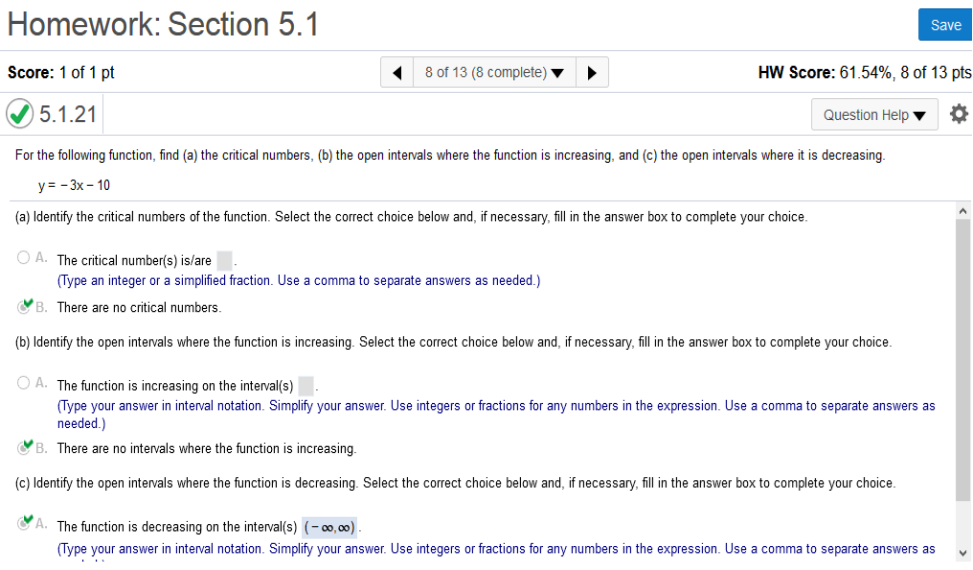
Check https://www.emathhelp.net/calculators/calculus-1/function-calculator/ For the function below, find a) the critical numbers; b) the open intervals where the function is increasing; and c) the open intervals where it is decreasing. 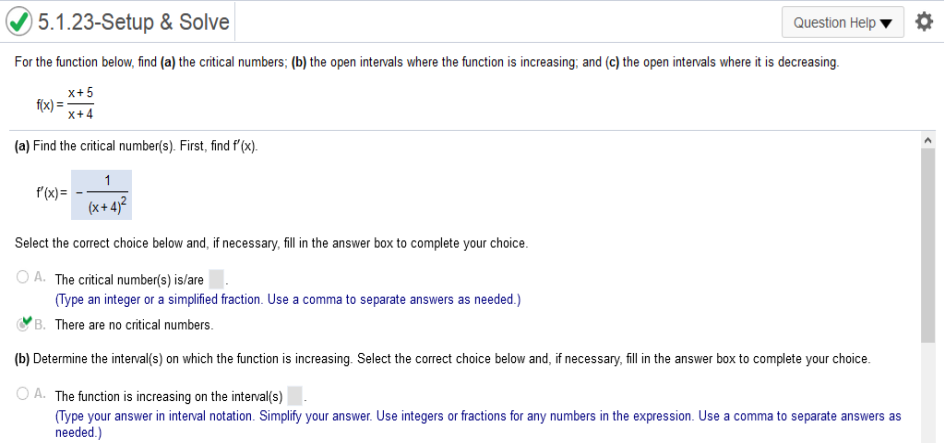 
For the function below, find a) the critical numbers b) the open intervals where the function is increasing c) the open intervals where it is decreasing. f(x) = (x + 7)2/3 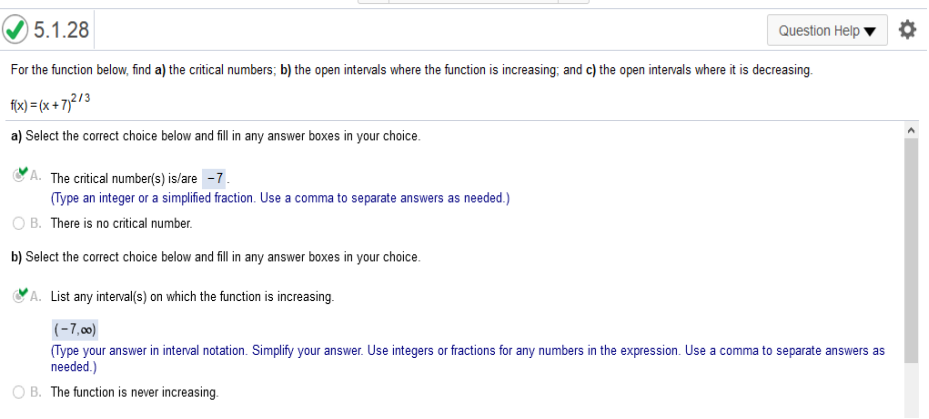 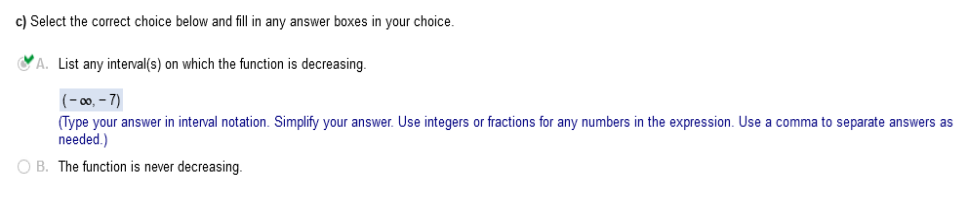
https://www.emathhelp.net/calculators/calculus-1/function-calculator/ a = Intervals of Increase = first number b = Intervals of Increase c = Intervals of decrease Find derivative and value of x = 0 
Suppose the total cost C(x) (in dollars) to manufacture a quantity x of weed killer (in hundreds of liters) is given by the function. C(x) = x3 – 4x2 + 9x + 50 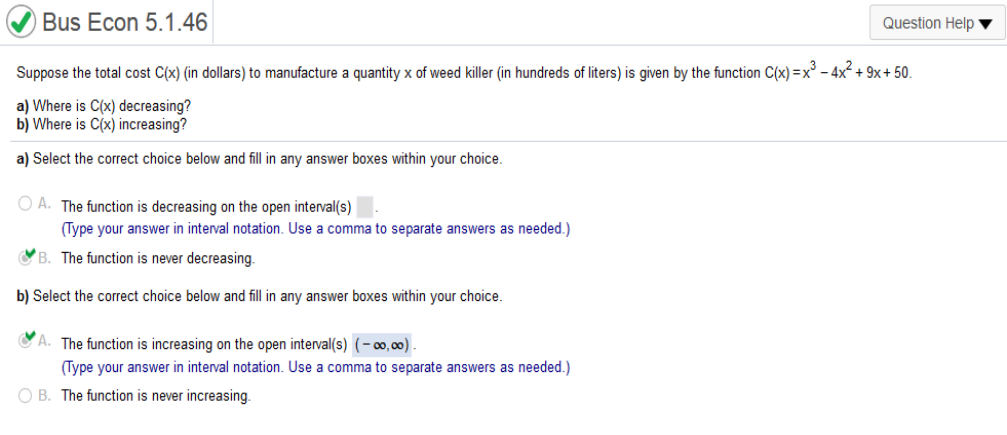
You can graph this or check https://www.emathhelp.net/calculators/calculus-1/function-calculator/ x^3– 4x^2+9x+50 Scroll down to Critical Points Local Minima Local Maxima A manufacturer sells video games with the following cost and revenue functions (in dollars), where x is the number of games sold. Determine the interval(s) on which the profit function is increasing. 
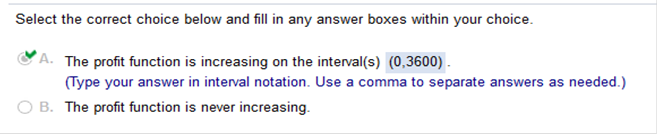
R(x) – C(x) .326x2 - .11x2 = .216x2 .0002x3 - .00016 = .00004x3 .216x2 - .00004x3 find the derivative of .216x2 - .00004x3 = .432x - .00012x2 .432x - .00012x2 = 0 x = 0 or x = 3600 answer = (0,3600) Find the locations and values of all relative extrema for the function with the graph below. 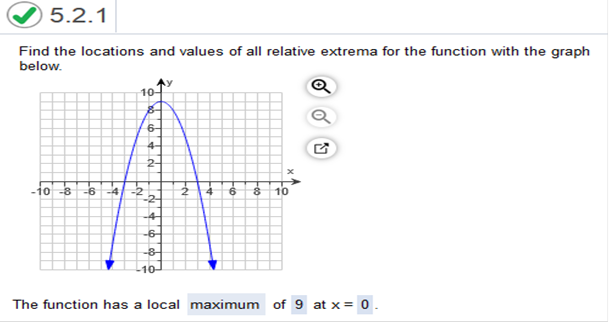
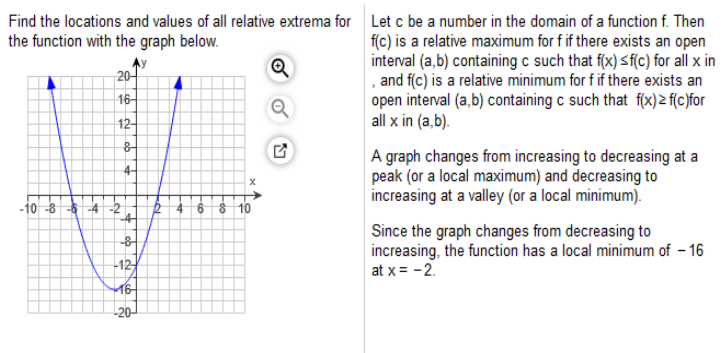
Study the graph 

Study the graph Find the locations and values of all relative extrema for the function with the graph below. 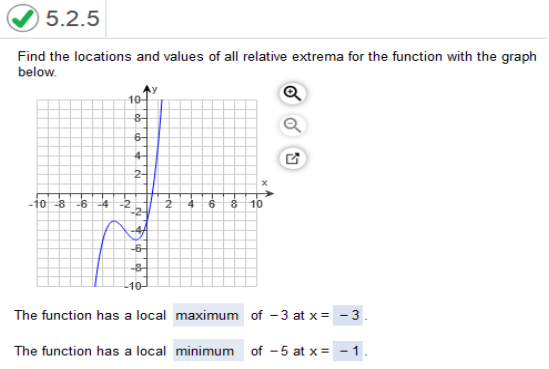
Study the graph 
Study the graph 
Study the graph Find the locations of all relative extrema and tell whether each extremum is a relative maximum or minimum. 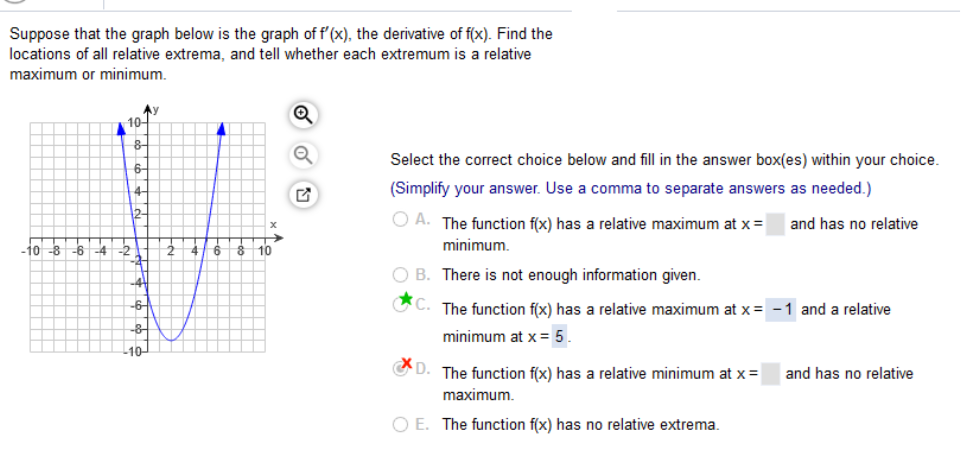
Study the graph Find the locations of all the relative extrema and tell whether each extremum is a relative maximum or minimum. 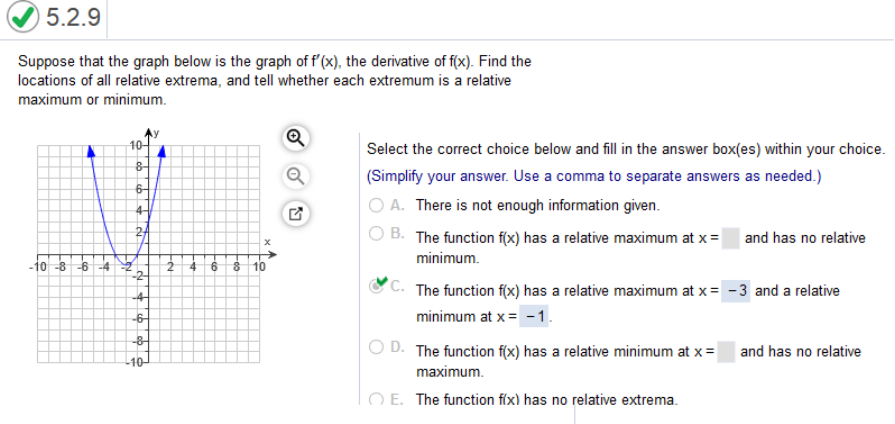
Study the graph f(x) = -x3 – 3x2 + 9x - 1 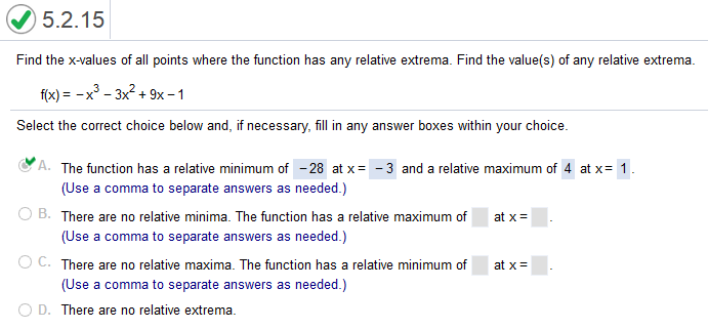
Long way: Find derivative of f(x) = -x3 – 3x2 + 9x – 1 = -3x2 – 6x + 9 Set equation = zero -3x2 – 6x + 9 = 0 https://quickmath.com/ enter -3x^2–6x+9=0 x = 1, -3 Plug in the values of x Maximum -(1)3 – 3(1)2 + 9(1) – 1 = 4 Minimum -(-3)3 – 3(-3)2 + 9(-3) – 1 = -28 Check https://www.emathhelp.net/calculators/calculus-1/function-calculator/ -x^3 – 3x^2 + 9x - 1 enter equation then, Local Maxima Local Minima f(x) = x3 – 3x2 – 24x - 4 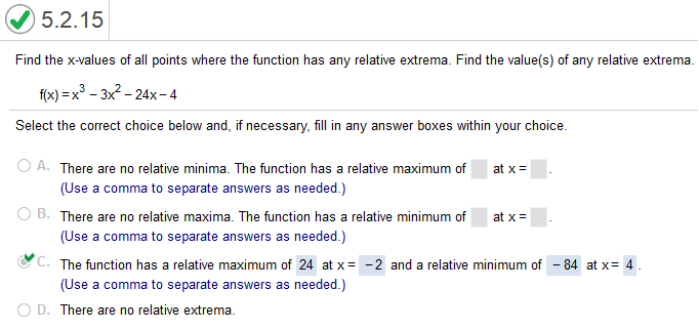
This is the same. Find the derivative of x3 – 3x2 – 24x – 4 = 3x2 – 6x – 24 Set = 0 3x2 – 6x – 24 = 0 https://quickmath.com 3x^2-6x-25=0 x = -2, 4 (-2)3 – 3(-2)2 – 24(-2) - 4 Check https://www.emathhelp.net/calculators/calculus-1/function-calculator/ You want to enter x^3-3x^2-24x-4 Local Maxima Local Minima f(x) = x4 – 32x2 - 2 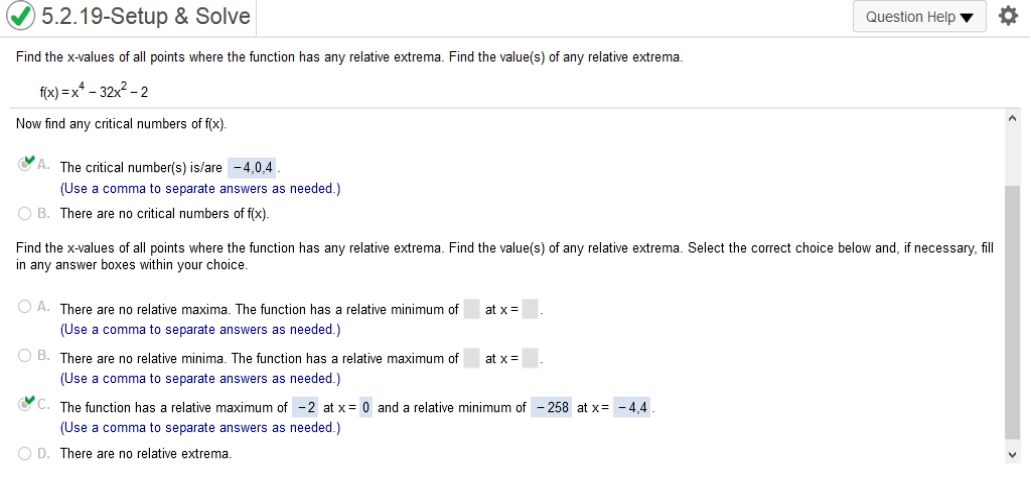
First find the derivative of f(x) 4x3 – 64x https://www.emathhelp.net/calculators/calculus-1/function-calculator/ enter equation then, Critical Points (x = first numbers) Local Maxima First number is x second number is maximum. Local Minima First numbers are x values, second are minimums F(x) = 8 – (3 + 3x)2/3 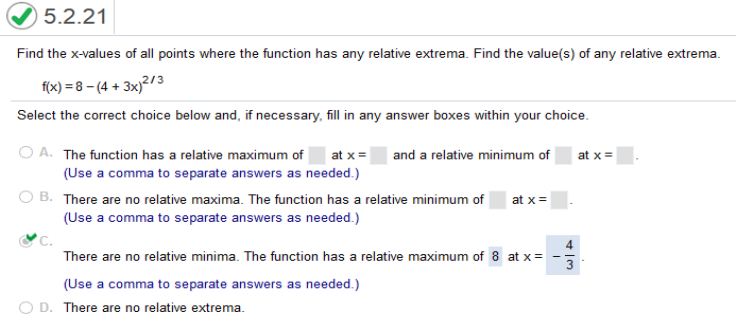
https://www.emathhelp.net/calculators/calculus-1/function-calculator/ enter equation then, Local Maxima First number is x second number is maximum. Local Minima First numbers are x values, second are minimums. 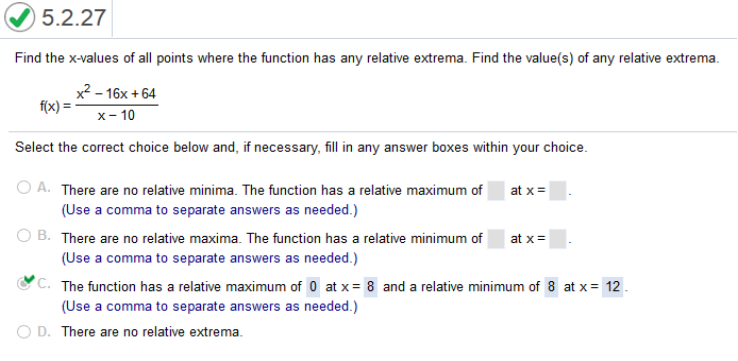
https://www.emathhelp.net/calculators/calculus-1/function-calculator/ (x^2–16x+64)/(x–10) Local Maxima First number is x second number is maximum. Local Minima First numbers are x values, second are minimums. f(x) = -7x – 4 ln(x) 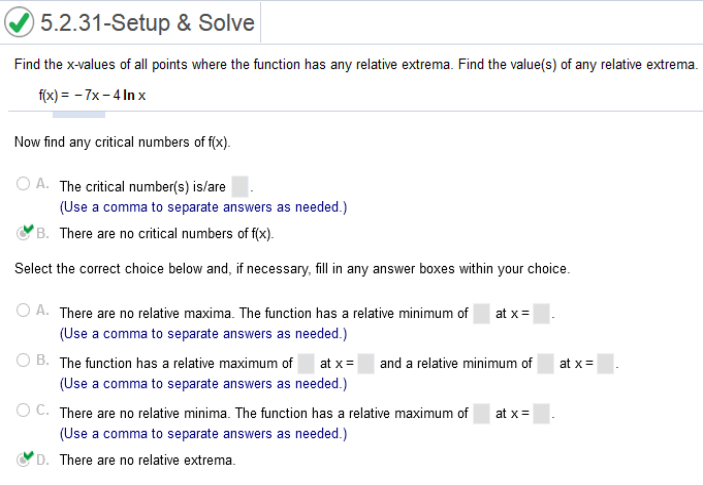
Find the derivative -7x – 4 ln(x) The derivative of ln(x) with respect to x is So, the derivative = Check https://www.emathhelp.net/calculators/calculus-1/function-calculator/ enter equation in () Critical Points Local Maxima First number is x second number is maximum. Local Minima First numbers are x values, second are minimums. Homework Chapter
1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM Need A Tutor? Need Homework Help?
|
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |