Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel

Use the quotient rule to find the derivative of the function.
f(x) =    


 


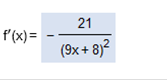
The quotient rule states that the derivative of) [] =  

Now let’s establish some of the rules.         f = the numerator     g = the denominator
f’ is F prime (which is the derivative of f)
g’ is G prime (which is the derivative of g)

In this case
f = 3x + 5 and f’ (f prime or derivative) = 3
g = 9x + 8 and g’ (g prime or derivative) = 9

So, we can start to plug the values in, factor, and solve!
 
So far, we have
f = 3x + 5
g = 9x + 8
f’ = 3
g’ = 9
we can now plug the values into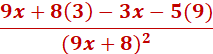  

Now we can simplify. *We do not need to simplify the bottom.
9x + 5(3) = (27x + 24) – 3x - 5(9) = (-27x - 45) (since we are subtracting , both values will need to be negative)
So, we are left with 27x – 27x + 24 – 45 (we will group by common terms)
27x – 27x + 24 – 45
27x – 27x = 0
24 – 45 = -21
Now we can put the equation back together
(remember we did not need to factor or simplify the denominator (9x + 8)²
The answer is
   
Find the derivative of the function.
y =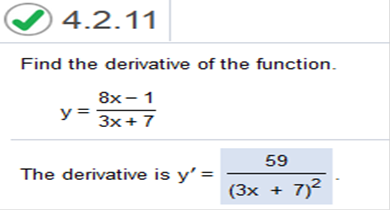
 

We would do the same as above. You will have to solve quite a few of these, so focus and practice.
One thing you need to remember is the values of fg’ will need to be negative!
 
The quotient rule states that the derivative of) [] =  

Now let’s establish some of the rules.
f = the numerator
g = the denominator
f’ is F prime (which is the derivative of f)
g’ is G prime (which is the derivative of g)
In this case
f = 8x - 1
g = 3x + 7
f’ = 8               (the derivative of f)
g’ = 3              (the derivative of g)
Now we can plug the values into  (t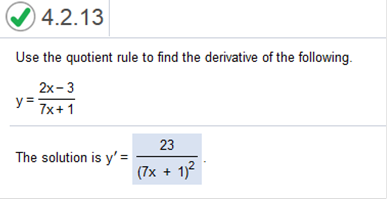he values of fg’ will need to be negative)
 
 =  =  =

Use the quotient rule to find the derivative of the following.
y =
 

This is the same procedure as above.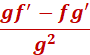

 
f = 2x - 3
g = 7x + 1
f’ = 2               (the derivative of f)
g’ = 7              (the derivative of g)
 
The answer is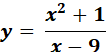
  Use the quotient rule to find the derivative of the function.

Ti-nspire

This is the same procedure as above; however, the expressions are a little different,
So, I will list the steps to solve it for you. It will be best if you list the values like do below.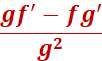

 
f = x² + 1
g = x - 9
f’ = 2x            (the derivative of f)
g’ = 1              (the derivative of g)
We know what g² is. it is (x – 9)²
 =  =  =
   
Use the quotient rule to find the derivative of the following.

 
 


 
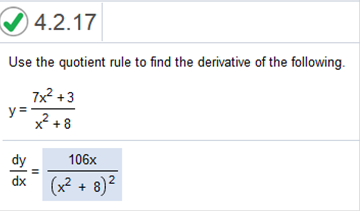
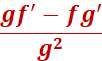
f = 7x² + 3
g = x² + 8
f’ = 14x                      (the derivative of f)
g’ = 2x                        (the derivative of g)
We know what g² is. it is (x² + 8)²
 =
   
Use the quotient rule to find the derivative of the following.


First we need to factor and simplify f (the numerator)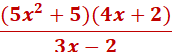

5x²(4x) = 20x³
5x²(2) = 10x²
5(4x) = 20x
5(2) = 10
So, we have f = 20x³ + 10x² + 20x – 10. We can rewrite the equation now.
 

 

 
f =
g = 3x - 2
f’ = 60x² + 20x + 20            (the derivative of f)
g’ = 3              (the derivative of g)
We know what g² is. it is (x² + 8)²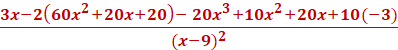
 
   
The total cost​ (in hundreds of​ dollars) to produce x units of a product is c(x) =  .
Find the average cost for each of the following production levels.
 
a.       20 units
b.       x units
c.       Find the marginal cost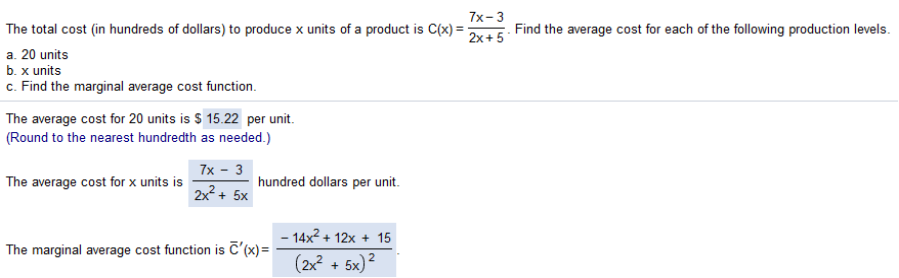
 

 
a.      15.22
 
b.  
.
c.      
 
a.      7(20) – 3/2(20) + 5 = 137 / 45 = menu | number | convert to decimal = 3.04444(100) / 20 = 15.2222 (round to 15.22)
b.   () =
   
A psychologist contends that the number of facts of a certain type that are remembered after t hours is given by the following function.

 

We use the quotient rule to differentiate the function. Then we plug the values in to solve it.
 

 

We use the same procedure as we have been using.
f = 92t
g = 99t – 92
f’ = 92
g’ = 99
 
so, we know g² = (²               now we need to factor gf’ – fg’
 
 
 
99t(92) = 9108t
-92(92) = -8464
 = 9108t
So we are left with     9108t – 9108t – 8464 which = -8,464 (there is no need to plug in any values)
Now we plug in the value 1 into g² []  99(1) – 92² = 7², and 7² = 49
So we are left with -8464 / 49
-8464 / 49 = -172.734 (-173)
 
 
 
Plug in 10 round to the nearest integer which equals 0
   
Write the function as a composition of two functions.
y = (1 – x²)^3/8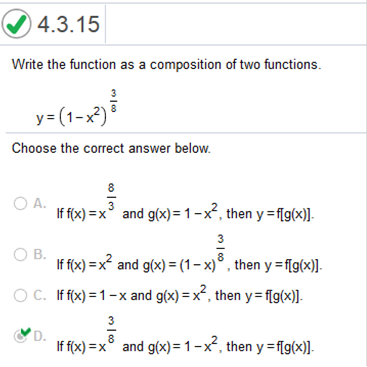
 
 
Write the function as a composition of two functions.
y = -√14 + 4x
 
Find the derivative of the function
y = (9x⁴ – 3x² + 7)⁴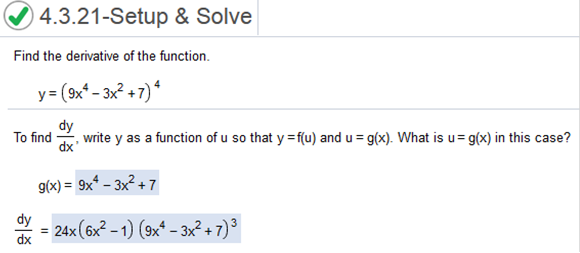
 

Explanation
First, we multiply
4 (9x⁴ – 3x² + 7)^{4 – 1} =         4 (9x⁴ – 3x² + 7)³
Next, we find the derivative of 9x⁴ – 3x² + 7 =         36x³ – 6x
Now we set up the equation and simplify
4(36x³ – 6x) (9x⁴ – 3x² + 7)³
Now we simplify the left side.
24x (6x² – 1) (9x⁴ – 3x² + 7)³
 
Check
https://www.derivative-calculator.net/
(9x^4-3x^2+7)^4
   
Find the derivative of the function
y = (5x⁴ – 7x² + 8)⁴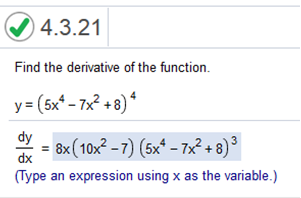
 

Explanation:
Same steps as above
4(5x⁴ – 7x² + 8)^{4 – 1} =          4(5x⁴ – 7x² + 8)³
Find the derivative of        5x⁴ – 7x² + 8 =         20x³ – 14x
Now we set up the equation and simplify
4(20x³ – 14x) (5x⁴ – 7x² + 8)³
We simplify this à 4(20x³ – 14x) take a close look at the answer.
We will subtract 1 from the exponent, multiply 4(2x) and divide -14 / 2
The answer is          8x (10x² – 14x) (5x⁴ – 7x² + 8)³
  Find the 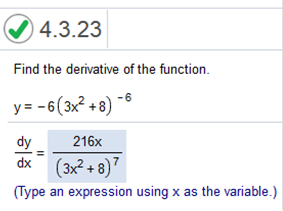derivative of the function
y = -6 (3x² + 8)^-6
 


First, we can see that the answer will be a fraction, so we need to look at the denominator (bottom) first.
The denominator will always be this part -> (3x² + 8)^-6, however, we will need to subtract 1 from the exponent.
So, the denominator will be (3x² + 8)^{-6 – 1} which equals (3x² + 8)^-7
And remember, it will be positive, because we are moving it to the bottom of the fraction.
We have the denominator which is (3x² + 8)⁷
The numerator is rather simple; however, you really need to focus on what I am doing here.
You will see that I use the same principle below.
The numerator will be -6 · -6 because we are multiplying the -6 exponent by the first part of the equation.
So now we have -6 · -6 = 36
Now we take the derivative of 3x² which is 2 · 3x which equals 6 x
So, we have 36 · 6x which equals 216x.                    The numerator = 216x           the denominator = (3x² + 8)⁷
Problem solved. Now we put the answer together.
 

   
Find the derivative of the function
s(t) = 42(2t³ – 9)^6/5


We do the same with this, however, we have an exponent which is a fraction, and in the case,
we use the numerator of the fraction. This is a bit different in that we will not move the whole exponent to the bottom, because
the exponent will be a fraction. We can use the same trick though.
We subtract 1 from the outer exponent first. 6/5 – 1 = 6/5 – 5/5   = 1/5.
Since we are subtraction, we must move 5 to the bottom. You may ask why? That’s because we are dividing 6/5 – 5/5.
We need to leave 5 at the bottom. So, we have the denominator. Which = 5
Now for the numerator. We only use the 6 from 6/5, and we already have the outer exponent, which = 1/5
We simply factor like so,
6(42) times the derivative of 2t³
Let’s find the derivative of 2t³ first which = 6t²
So, we have 6 · 42 · 6t² = 1512t²

Please study my answer carefully.
   
Find the derivative
f(x) = 4√3x² + 5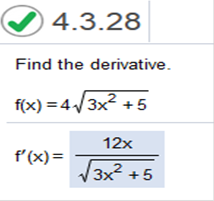
 

 
This is simply 4(3x) divided by √3x² + 5 =     
Simplified it would be  however, this answer uses square root.
   
Find the derivative
 

We can use a shortcut with this one also.
We find the derivative of 7x⁵ + 5 which =     35x⁴
We need to use the outer exponent on the bottom (denominator), however we will be moving it up, so it will be negative
And we will be subtracting 1 the same as we have been doing. We will be moving it down again, so keep that in mind.
So, we have
35x⁴ · (-5 · -3) = 35x⁴(15) = 525x⁴ (we used the -5 on top, the negative outer exponent from the bottom, and the derivative of 7x⁵ + 5)
We have the numerator which = 525x⁴.
The denominator is the same as the equation we were asked to solve however, we needed to subtract 1 from the outer exponent after we moved it up,
The exponent was then -3 then we subtracted 1 and ended up with -4. We needed to move it back down, so it is ⁴
So the answer is:

   

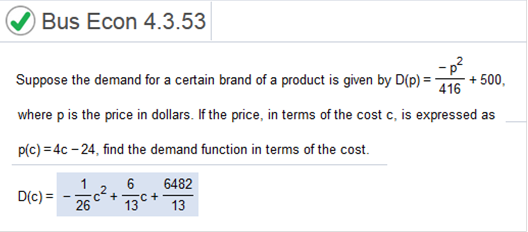
Suppose the demand for a certain brand of a product is given by  D(p) where p is the price in dollars.
If the​ price, in terms of the cost​ c, is expressed as   find the demand function in terms of the cost.
 
Rewrite equation
-(4c – 24)² / 416 + 500
   
To test an​ individual's use of a certain​ mineral, a researcher injects a small amount of a radioactive form of that mineral into the​ person's bloodstream. The mineral remaining in the bloodstream is measured each day for several days. Suppose the amount of the mineral remaining in the bloodstream​ (in milligrams per cubic​ centimeter) t days after the initial injection is approximated by
 
-0.01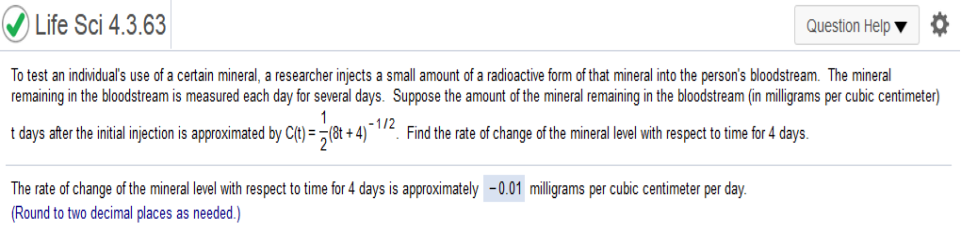
 

 
Find the derivative of ½(8t + 4)^-1/2
Then plug in the value of 4 (days)
   
Find the derivative of the function.
y = e^10x
What rule should be used to​ differentiate?

The first part
gives you the formula for finding derivatives with exponents and variables (x, t, etc…)
 
The second part.
Since the value of x is present as an exponent, we would use 10 to find the derivative and leave the rest the same.
So, it is 10(e^10x) = 10e^10x  
Differentiate the following function.
F(x) = 5e^5x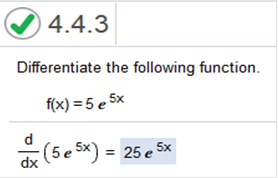
 

 
This is explained above.
Since the value of x is present as an exponent, we would use 5 to find the derivative.
So, we multiply 5(5) which = 25 and leave the rest alone.
The answer = 25e^5x
   
Find the derivative of the function.
f(x) = -5e^{-2x + 2}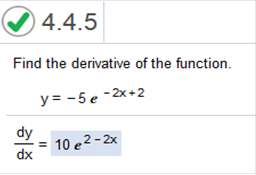

This is the same as above.
Since the value of x is present as an exponent, we would use -2 to find the derivative.
So, we would multiply -2(-5) which = 10 and leave the rest alone.
The answer has some values swapped, but it is the same.
The answer is 10e^{2 – 2x}
   
Differentiate the following function.
y = _ex⁴

We simply find the derivative of x⁴ and multiply it by _ex⁴
The derivative of x⁴ = 4x³
Now we multiply by _ex⁴
4x³(_ex⁴)
   
Find the derivative of the function.
_{y = 2e}-3x²
 
find derivative ti-npire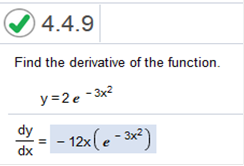
 

   
Find the derivative of the following function.
y = 10^{5x + 1}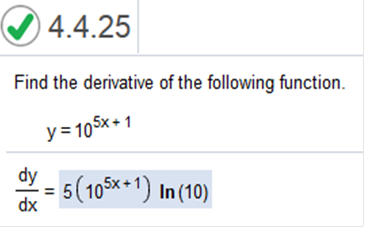
 

 
Differentiate using the chain rule, which states that
 [f(g(x))] is f'(g(x)) g'(x) where f(x) = 10x and g(x) = 5x + 1
 
ln (10) · 10^5x+1 · [5x + 1]
ln (10) · 10^5x+1 · [5 + 0]
Now simplify
5(10^{5x + 1}) ln(10)
   
The sales of a new​ high-tech item​ (in thousands) are given by
S(t) = 97 – 80e^-0.2t
 
Find the derivative and plug in the year values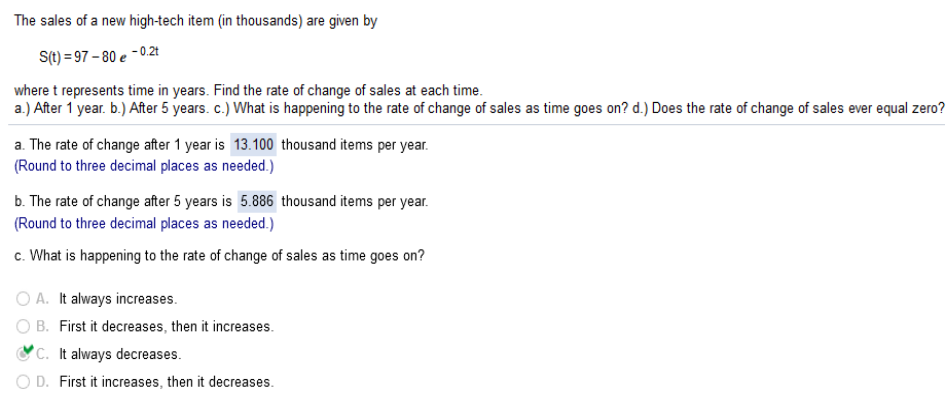

Part a.
We need to find the derivative of 97 – 80e^-0.2t and plug in the value (1 year).
What we do here is simple. We multiply -0.2(80e) which = 16e.
We leave the rest alone, so the derivative of 97 – 80e^-0.2t =          16e^-0.2t
Now we plug in the value. 16e^-0.2(1) (you will need a calculator for e)
The answer is 13.09969205 (round to 13.100)
 
Part b.
We simply plug in the value 5 like so
16e^-0.2(5) use a calculator.
The answer is 5.886071059 (round to 5.886)
Part c.
If you haven’t noticed, the rate of changed decreased from 1 year to 5 years.
 
Part d.
Common sense here.
 
The projected population of a certain ethnic​ group (in millions) can be approximated by p(t) =
35.54(1.024)^t where t = 0 corresponds to 2000 and 0 ≤ t ≤ 50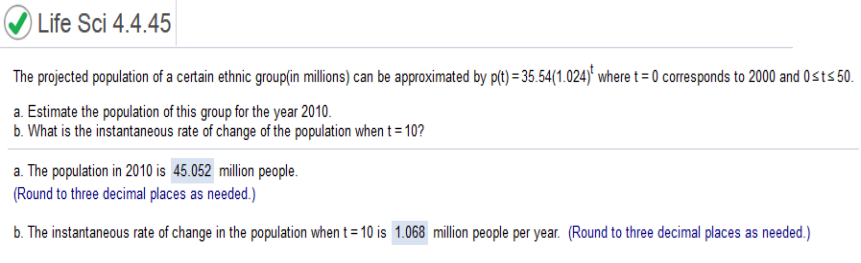
 

Explanation:
you can use a TI84 Plus calculator and enter exactly what I have.
a. 35.54 (1.024)¹⁰
b. 35.54ln(1.024)1.024¹⁰
   
Differentiate
f(x) = ln(10x)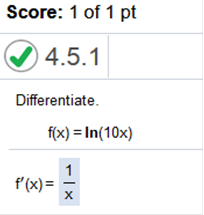
 

The easiest way to do this is to find the derivative of 10x, which = 10
Then we must divide by 10 + x (not 10x because ln cancels it out).
So, we are left with
 

 
Now we divide 10 by 10 which = 1
 
    is the answer
   
Differentiate
                            y = ln|4x² – 5x|
 
find the derivative of 4x² – 11x
then divide by 4x² – 11x
 

The derivative of ln(u) =
u’ is u prime or the derivative of u.
u’ = 8x – 5
u = 4x² - 5x
the answer is
   
A friend concludes that because y equals ln 6x and y = ln x have the same​ derivative, namely dy/dx = 1/x,
these two functions must be the same. Explain why this is incorrect. Choose the correct answer below.
 
A. A derivative shows the function at a certain point. Even though the function y equals ln 6 xy = ln6x and y equals ln xy = lnx
have the same​ derivative, the derivative only shows that the functions are the same at a certain point.
B. A derivative is a measure of how a function changes as its input changes. It is incorrect because the derivative shows how the functions change at an equal​ rate, not that the functions are the same.
C. A derivative shows the​ function's y-intercepts. Even though the function y equals ln 6 xy=ln6x and y equals ln xy=lnx
have the same​ derivative, the derivative only shows that the functions have the same​ y-intercepts.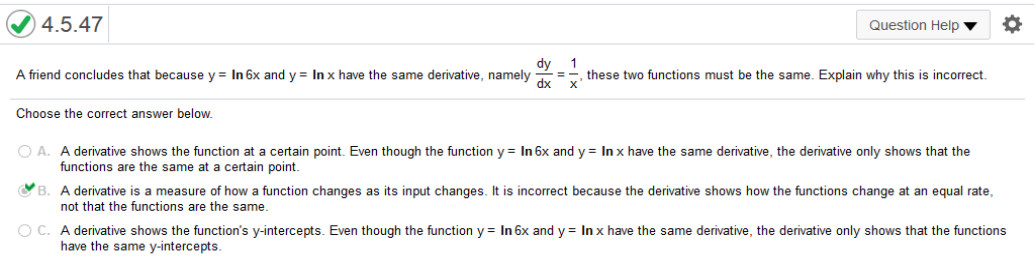

 
This is self-explanatory!
   
If total revenue received from the sale of x items is given by ​R(x) = 30 ln (2x+1)​,
while the total cost to produce x items is ​C(x) = ​, find the following.
​(a) The marginal revenue
​(b) The profit function​ P(x)
​(c) The marginal profit when x = 60
​(d) Interpret the results of part​ (c).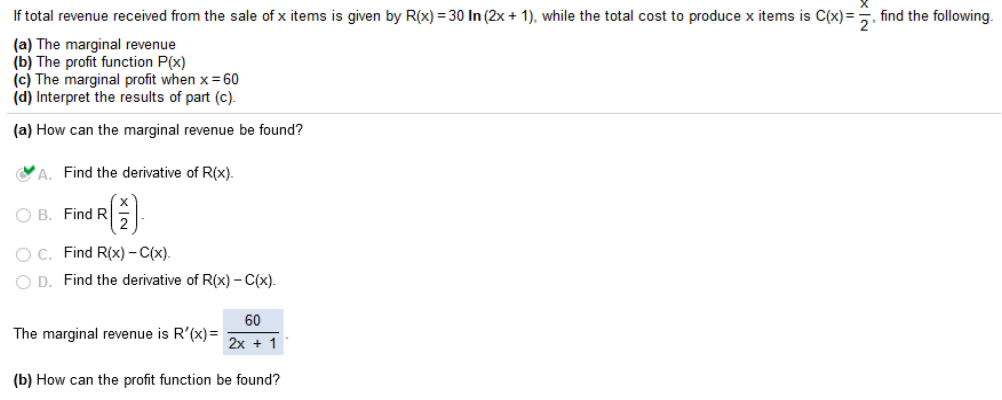
  
The answers are self-explanatory
   
Find the indicated derivative f(u) = 3u^0.8 – 2u^2.2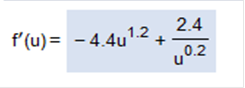
 

We can break this down and find the derivative very easily.
3u^0.8 – 2u^2.2
.08(3u)^{.08 – 1} = 2.4u^-0.2
2.2(-2)^{2.2 – 1} = -4.4^1.2
We need to convert 2.4u^-0.2 to fraction form because the exponent is negative
2.4u^-0.2 =        
Now we can put the equation back together in proper order.
-4.4^1.2 +
   
Find the derivative of the function.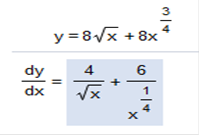

 
First, we would need to covert 8√x to a fraction.
The fraction form of 8√x =     8x^1/2    so now we can rewrite the equation
We need to find the derivative of 8x^1/2 + 8x^3/4 so this is how we do that.
 
(8x)^{1/2 – 1} = 4x^-1/2

(8x)^{3/4 – 1} = 6x^-1/4
 
Now we need to convert back to a fraction because the exponents are negative.
Remember, the square root of x is x^1/2.
We have x^-1/2, so we can rewrite that as  and 6x^-1/4 can be rewritten as
The answer is

 
Find the derivative of the function
15x² – 3x – 9x^-2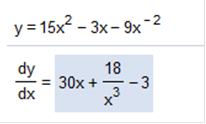

15x² – 3x – 9x^-2
15(2)^{2 – 1} = 30x
-3x(1)^{1 – 1} = -3
-9x(-2)^{-2 – 1} = 18^-3  = 18/x³ (We will need to convert this to fraction form)
 - 3
   
Find the derivative of the function.
y =  -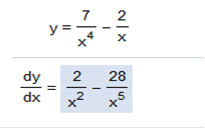
 

The process for this problem is long, and quite frankly, prone for mistakes.
SO, I have a shortcut once again to cut the time down considerably.
You can solve this problem one of two ways.
You can move the variables and exponents up or we can leave the exponents on the bottom and add.
This is the similar shortcut that I use on the other problems.
I will solve it by moving the exponents up.
Let’s start with  by moving x⁴ on top.

We do not need to use a negative except for the exponent, because we will move the variable and exponent back down.
So, this is all we need to do 7x^{-4 – 1}, find the derivative of 7x⁴ and we get 7x^-5, 28x.
We are moving the variables and exponents back down, so we have
We do the same with        2x^{-1 – 1}, find the derivative of 2x and we get 2x^-2, 2.
We are moving the variables and exponents back down, so we have
We can swap the expressions, so the answer =  -
   
Find the derivative of the function.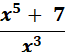

 

 
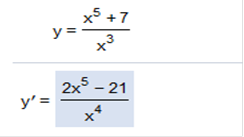
This is a difficult problem to solve, however, I will try and simplify it as much as possible.
Try and focus on it very carefully.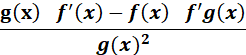
 

 
g(x) = x³
f(x) = x⁵ + 7
f’(x) = the derivative of x⁵ + 7 which = 5x⁴
f’ g(x) = the derivative of x³ which = 3x²
 
so, we have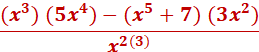

 
Staring from top left, we multiply x³(x4) = x⁷ and separate 5 and move to the left.
We can combine 5(x⁷), and multiply x²⁽³⁾ = x⁶)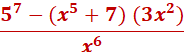

 
Next, we can move 3 (from 3x²) to the left following the minus sign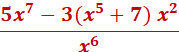

 
Next, we can factor x² out of x⁷ on top (we do this to create a common term on top and bottom)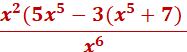

Now we can cancel some common factors (x², and x⁶) Watch closely at the remaining equation!
 =
 
Now we can simplify. Let’s factor the right side before doing so.
 

(subtract 5x⁵ – 3x⁵ = 2x⁵)
The answer =
   
Find the derivative of the function.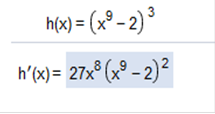

This is the formula that we have been working on above,
However, we can use the same shortcut with this as we have above.
Shortcut
We find the derivative of x⁹ – 2 which is      9x⁸
The exponent on the right side of the exponent is 3, so we can do this in one equation.
Focus on what I have done below.
(x⁹ – 2) stays the same, 3 is multiplied by 9x⁸, and we need to subtract 1 from the outer exponent.
 
3(9x⁸) + (x⁹ – 2)^{3 – 2} =          27x⁸(x⁹ – 2)²

---

---