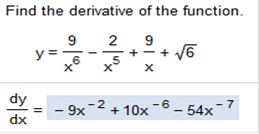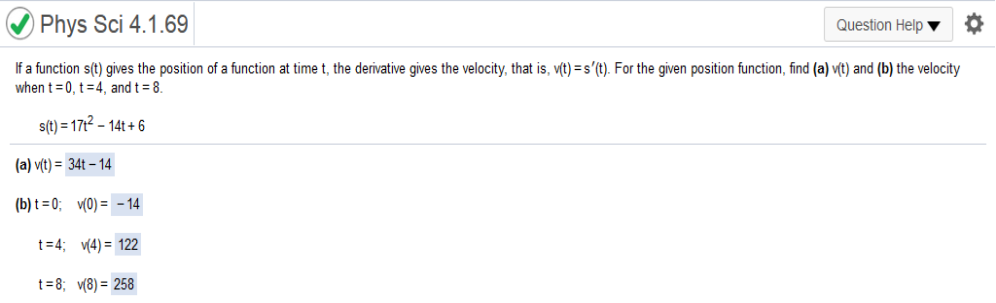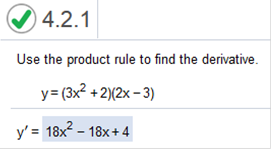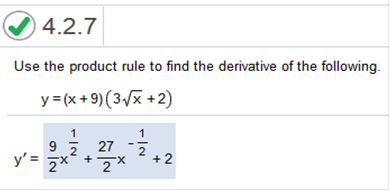Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel

Find derivative of the function: y = x³ – 4x² + 5x + 2

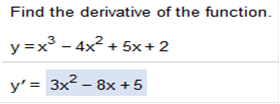
x³ · n^-1 =     3 · x^{3 – 1} =   3x²
4x² · n^-1 =   2 · 4x^{2 – 1} = 8x
5x · n^-1 =    1 · x^{1 - 1} =    5
2 · 0 =        0 Fin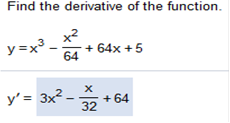d the derivative of the function.
y = x³ – 
 

 
Find the derivative. This is the same as above.
x³ – 
 
x³ –  x²) + 64 + (5)                  =          3x² -  + 64 + 0

Now we simplify
3x² - 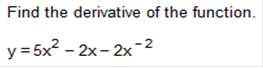 + 64
  Find the derivative of the function:  y = 5x² – 2x – 2x^-2
 

 
dy/dx = 10x + 4x^-3 – 2
 
y = 5x²- 2x - 2x^-2
Find derivative of 5x² - 2x - 2x^-2
We can break this down.
The derivative of
5x²      =         10x
-2x      =         -1
-2x^-2    =     4x^-3
Now we put the equation back together in proper order.
5x² + 4x^-3 – 2
Please note: sometimes a term with a negative exponent will appear in fraction form.
In this case, 4x^-3 could  appear as
  Find the derivative of the function
 -

We need to find the derivative of the equation.
The easiest way for me is to move the exponents up to the numerator and find the derivative.
Then we would need to put the equation back into fraction form.
*2 Notes: When we move an exponent up to the top, the exponent is then negative.
The derivative of a negative exponent would mean to multiply a negative number add -1 to the negative exponent.
For example, if we have 2x^-2, the derivative would be -4x^-3 (fraction form )
 
Here are a few more examples, so you can get an idea of what is going on.
The derivative of    2x^-2 = -4x^-3    fraction form =
The derivative of    3x^-3 = -9x^-4    fraction form =
The derivative of    4x^-4 = -16x^-5 fraction form =
I like to move exponents on the bottom to the top,
Because it can become very confusing otherwise. The choice is up to you!
 
Here we go
 -  =       6x^-2 - 8x^-1
The derivative of 6x^-2 = -2(6x)^{-2 – 1} = -12x^-3 = fraction form
- 8x^-1 = -1(-8x)^{-1 -1} = 8x^-2 = fraction form         So, we are left with  

Find the derivative of the function

This is like the above problem; except we have a square root value.
The square root is eliminated anyway because there is no variable. The derivative of √6 = 0. No worries!
This is a little confusing as well because we will need to rearrange the order.
Just so you know, -1 is greater than -2, -3, and so because negative values closest to 0 come first, from left to right.
The greatest value comes first. The problem is not in order from the get-go.
I am going to do this the way I want again. Move exponents up to the top. I can actually do these in my head
And jot the number down as I go along, but it is a good idea to practice these on your own.
AND this answer will not be in fraction form, so we would need to convert the expressions anyway!
 =   9x^-6 – 2x^-5 + 9x^-1
 
Now all we need to do is break the equation down, find the derivative and rearrange.
 
Derivatives
9x^-6 =              -54x^-
-2x^-5=                        10x^-6
9x^-1 =              -9x^-2
The answer in proper order        -9x^-2 + 10x^-6 - 54x^-7 F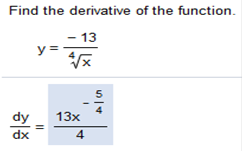ind the derivative of the function.
            y =
 

 
First, we can rewrite the equation and eliminate the radical (square root)
 

 
There are a few ways to do this, however we will stick to the way I showed you above.
Next, we can move the exponent to the top like we have been doing.
^-1/4
Now we can find the derivative. Watch closely at how I find the derivatives for each expression.
We would multiply -13 by  which is simple enough
 =
Next we must add -1 to  
which is the same as  =
Now we can put the equation back together


  Find the derivative of the function.     y =
 

 
This one is a little tricky, however, this is how I would solve it and find the derivative.

Please note we need to divide both expressions by x (or x¹) and x¹ will be negative as well.
Now we will move x to the top and remember anytime we move an exponent up
We must subtract it from a like term.
So, we have  or 4x²   and   9x^-1
Now we find the derivatives and put the equation back together.
the derivative of
the derivative of 9x^-1 x^-2
Since we can see the answer is in fraction form, we can move the variable and exponent down (it becomes positive again).
8x – 9x^-2 =          
 
Which of the following describes the derivative function f’(x) of a quadratic function f (x)​?
 
Answer:        Linear
 

   
Explain the relationship between the slope and the derivative of​ f(x) at x = a

Answer:          The derivative of​ f(x) at x = a equals the slope of the function at x = a.
  Find the slope of the tangent line to the graph of the given function at the given value of x.
Find the equation of the tangent line.
y = x⁴ – 2x³ + 9; x = 1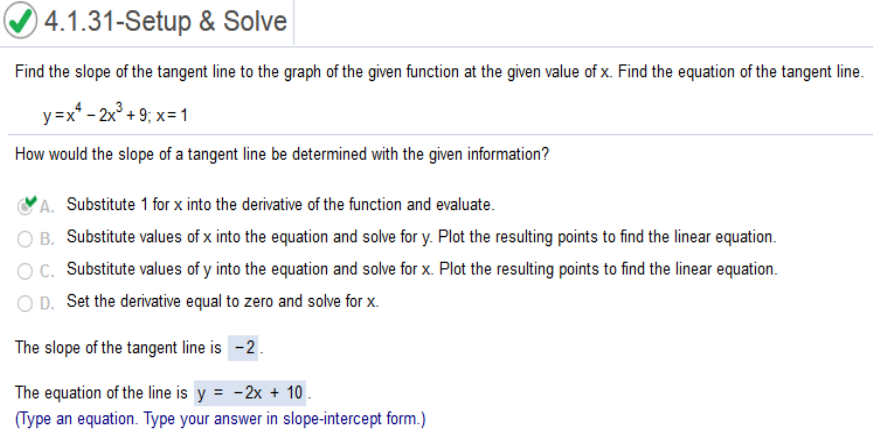
 

y = x⁴ – 2x³ + 9, x = 1
First, we need to find the derivative of            y = x⁴ – 2x³ + 9 = 4x³          =          4x³ – 6x²
plug in the value of x = 1             4(1)³ – 6(1)² =           -2             Slope = -2
y = mx + b                -2(1)
y = (1)⁴ -2(1)³ + 9 = 8
8 = -2(1) + b
8 = -2(1) + b = add 2 to both sides
b = 8 + 2 = b = 10
y = -2x – 10
https://www.mathepower.com/en/tangent.php
Find the slope and the equation of the tangent line to the graph of the function at the given value of x
f(x) = x⁴ − 25x² + 144; x = 2
 
The Slope tangent line is -68
(Simplify your answer)
 
The Equation of the tangent line y = -68x + 196

 
Find the derivative of f(x) = x⁴ −25x² + 144 = 4x³ – 50x
Plug in x = 2 4(2)² – 50(2) =          The slope of the tangent line is -68
y = (2)⁴ – 25(2)² + 144 = 60
the tangent line passes through the point (2,60) and has slope -68
 
y – y1 = m(x – x1)
y – (60) = -68(x – (2))
y = -68x + 136 + 60
The equation of the tangent line is y = -68x +196

Cool calculator
enter equation
https://www.mathepower.com/en/tangent.php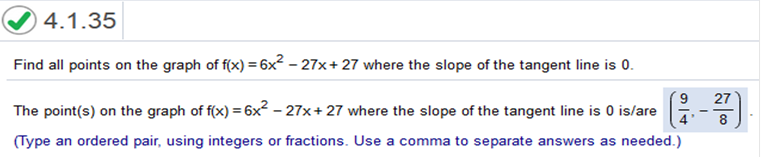
  Find all points on the graph of ​f(x) = 6x² – 27x + 27 where the slope of the tangent line is 0.
 

Find the derivative of 6x² – 27x + 27
f(x) = 6x² – 27x + 27 =                    12x – 27
set to equal 0                                  12x – 27 = 0 =                      9/4
Plug in x to find the y slope         f(9/4) = 6(9/4)² – 27(9/4) + 27 = -27/8
x = 9/4, y = -27/8
points on the graph = (9/4, -27/8)
 
https://www.emathhelp.net/calculators/calculus-1/function-calculator/
enter equation
Critical Points
(9/4, -27/8)
  Explain the concept of marginal cost. How does it relate to​ cost? How is it​ found?
How does the marginal cost relate to​ cost?
 
A. Marginal cost refers to the rate of change of cost.
B. Cost refers to the rate of change of marginal cost.
C. Marginal cost is the same as cost. Assume that a demand equation is given by q = 7000 - 100p Find the marginal revenue for the given
production levels​ (values of​ q).
(Hint: Solve the demand equation for p and use R(q) = qp​.)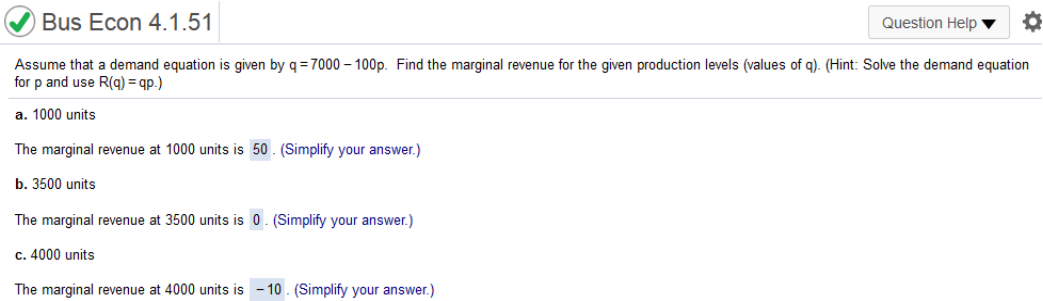

 
P = 7000 – q / 100
Rq = q (7000 – q / 100)
Rq = 70q – q² / 100
Find derivative of 70q – q² / 100 =     d/dq (70q – q² / 100) =         70 – q/50
Plug in 1000 units     70 – (1000 / 50) =    50
The marginal revenue at 1000 units is 50

3500 units             70 – (3500 / 50) =        0
4000 units             70 – (4000 / 50) =       -10
  The total amount of money in circulation for the years​ 1990-2012 can be closely approximated by
M(t) = 0.05026t³ - 1.125t² + 37.81t + 247.3
where t represents the number of years since 1990 and​ M(t) is in billions of dollars.
Find the derivative of​ M(t) and use it to find the rate of change of money in circulation in the following years.
 
What do your answers in parts​ a-d tell you about the amount of money in circulation in those​ years?
The amount of money in circulation in those years increases from 1990 to 2005.increases from 1990 to 2005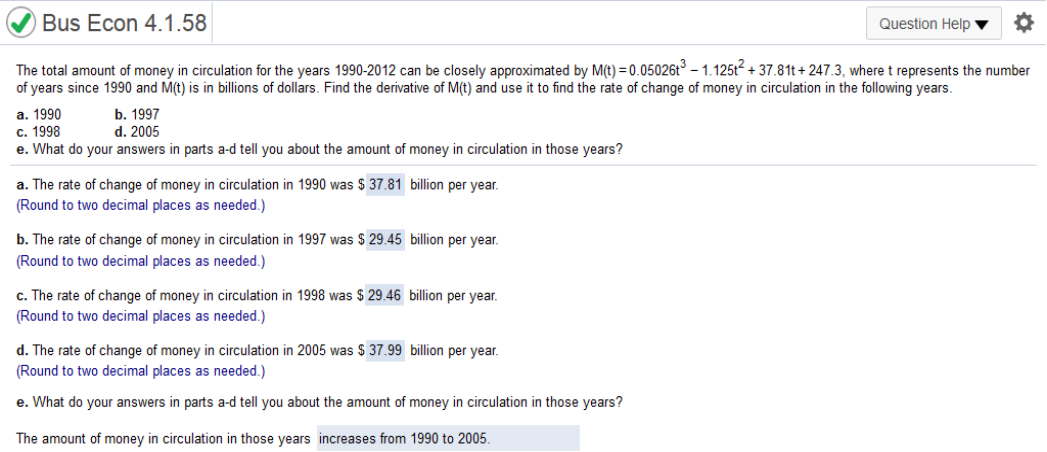

Find the derivative of 0.05026t³ - 1.125t² + 37.81t + 247.3 =     0.15078t² -2.25t + 37.81
Plug in 1990 – 1900 = 0             .15078(0)² -2.25(0) + 37.81 =        37.81
 
The rate of change of money in circulation in 1997 __ was ​billion per year.
Plug in 1997 – 1990 = 7             .15078(7)² - 2.25(7) + 37.81 = 29.4482 =   29.45
 
The rate of change of money in circulation in 1998 __ was ​billion per year.
Plug in 1998 – 1990 = 8             .15078(8)² - 2.25(8) + 37.81 = 29.4482 = 29.4599 =    29.46
 
The rate of change of money in circulation in 2005 __ was ​billion per year.
Plug in 2005 – 1990 = 15             .15078(15)² - 2.25(15) + 37.81 = 29.4482 =     37.99
  In 1906 Kennelly developed a simple formula for predicting an upper limit on the fastest time that humans could
ever run distances from 100 yards to 10 miles. His formula is given by =.0588s1.125 where s is the distance in
meters and t is the time to run that distance in seconds.
Find​ Kennelly's estimate for the fastest a human could possibly run 1603 meters.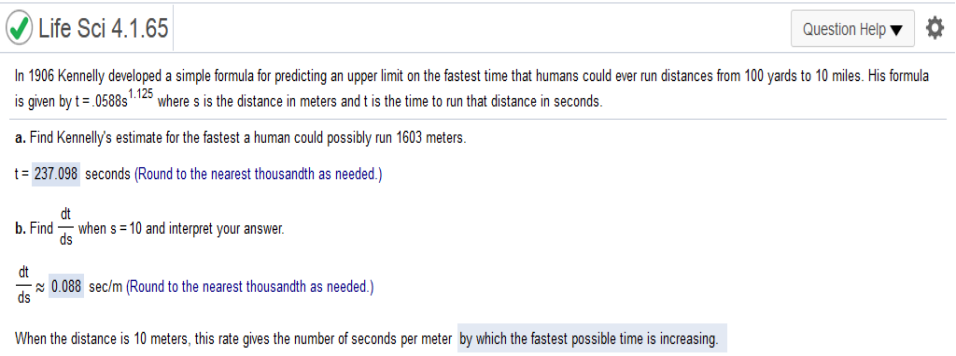

 
0.0588(1603)^1.125 =             237.098
 
Find dt/ds when s = 10 and interpret your answer.
Find the derivative of .0588s^1.125 = .06615s^.125
Plug in 10
.06615(10)^.125 =       0.088212

When the distance is 10 ​meters, this rate gives the number of seconds per meter

Answer:     by which the fastest possible time is increasing.

If a function s(t) gives the position of a function at time​ t, the derivative gives the​ velocity, that​ is, v(t) = s’(t).
for the given position function, find (a) v(t) and (b) the velocity when t = 0, t = 4, and t = 8
s(t) = 17t² – 14t + 6
 

Find the derivative of s(t) = 17t² – 14t + 6 =                34t – 14
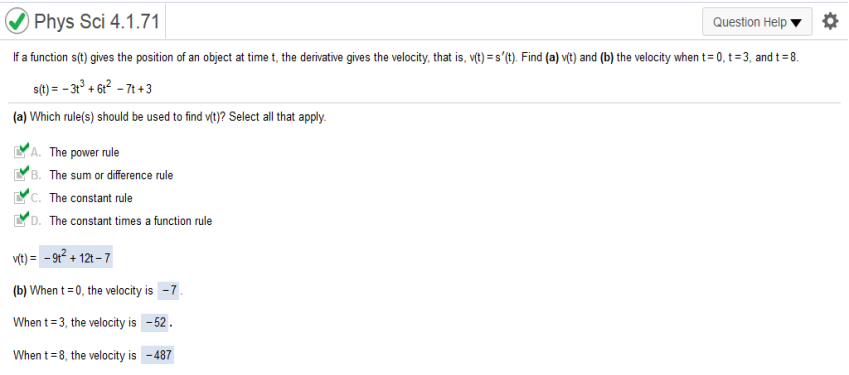
Then plug in the values of t.
If a function s(t) gives the position of a function at time​ t, the derivative gives the​ velocity, that​ is, v(t) = s’(t).
for the given position function, find (a) v(t) and (b) the velocity when t = 0, t = 3, and t = 8
s(t) = -3t³ +6t² -7t + 3
   If a function s(t) gives the position of an object at time t, the derivative gives the velocity, that is, v(t) = s'(t).
Find (a) v(t) and (b) the velocity when t = 0, t = 3, and t = 8.

Which​ rule(s) should be used to find​ v(t)? Select all that apply.
 
A. The power rule
B. The sum or difference rule
C. The constant rule
D. The constant times a function rule
 
Find the derivative of
-3t³ +6t² -7t + 3 =     -9t² + 12t – 7
Plug in the values of t
-9(0)² + 12(0) – 7
-9(3)² + 12(3) – 7
-9(8)² + 12(8) – 7
  Use the product rule to find the derivative of the function     y = (4x² + 5) (5x – 4)
 
Part 1
What is the correct way of writing the derivative of y?

Part 1 explanation:
This is the correct way of writing the derivative of y, however, I do not solve these types of problems that way.
The choice is up to you, but I can solve this problem in less than one minute my way.
The other way is confusing and requires much more simplifying.
Part 2    Whenever you see   the derivative of y was taken with respect to x
Okay, so we need to find the derivative of (4x² + 5) (5x – 4)
We factor (4x² + 5) (5x – 4) first.
4x²(5x) = 20x³             4x²(-4) = -16x²             5(5x) = 25x
5(-4) = -20 (we know that the derivative of -20 = 0 so we will cross this out)
We are left with 20x³ – 16x² + 25x
Derivatives of             20x³    3(20x)^{3 – 1} =   60x²
– 16x²                            2(-16x)^{2 – 1} = -32x
+ 25x  1(25x)^{1 – 1} =   25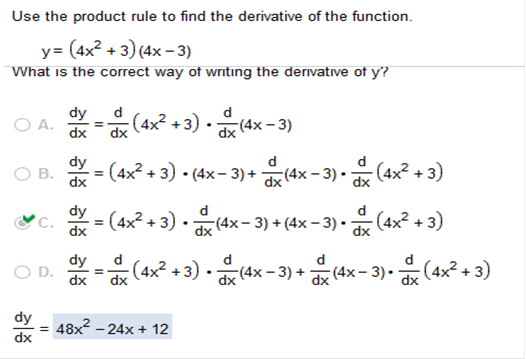
60x² – 32x + 25
  Use the product rule to find the derivative of the function.     y = (4x² + 3) (4x – 3)

 
There is nothing different about this than the problem we just solved.
We factor y = (4x² + 3) (4x – 3) first.
I will solve the next one. You can practice this one on your own.
The answer is: 48x² – 24x + 12 
Use the product rule to find the derivative     y = (3x² + 2)(2x – 3) 

We need to go back to College Algebra and reflect on factoring again.
Whever we see an equation like (3x² + 2) (2x – 3) in Calculus, we need to factor first.
First, we need to factor (3x² + 2)(2x – 3)
3x²(2x) = 6x³         3x²(-3) = -9x²         2(2x) = 4x         2(-3) = -6
This leaves us with 6x³ – 9x² + 4x – 6
Now we need to find the derivative of
6x³ – 9x² + 4x – 6
The derivative of 6x³ is 3(6) (x^{3 – 1}) or 18x²
The derivative of -9x² is 2(-9) (x^{2 – 1}) or -18x
The derivative of 4x is 1(4) (x^{1 – 1}) or 4
The derivative of -6 is 0
Now we put the derivative back in order.
18x² – 18x +4

Differentiate.        F(x) = (3x + 2)²

This is like the problem above except we are dealing with a square of an equation.
(3x + 2)² is the same as (3x + 2) (3x + 2)
The same as above
3x(3x) = 9x²
3x(2) = 6x
2(3x) = 6x
2(2) = 4
So, we are left with 9x² + 6x + 6x + 4 (simplified to) 9x² + 12 + 4
Now we need to find the derivative of 9x² + 12 + 4
2(9) (x^{2 – 1}) = 18x (x¹ is the same as x)
1(12) (x^{1 – 1}) = 12
The derivative of 4 = 0
So, the answer is 18x + 12 Use the product rule to find the derivative of the following.    y = (x + 9) (3√x + 2)

let u(x) = x + 9 then u’ = 1 (u’ is derivative)
let x(x) = 3√ + 2 then v’ = 3/2^-1/2 (v’ is derivative)
x + 9(3/2^-1/2) + 3√x + 2(1)
simplify
3/2x^1/2 + 27/2x^-1/2 + (3√x + 2)(1)
Simplify
3/2x^1/2 + 27/2x^-1/2 + 3x^1/2 + 2
Combine like terms.
3/2x^1/2 + 3x^1/2 = 9/2x^1/2
+ 27/2x^-1/2 + 2 =
9/2x^1/2 + 27/2x^-1/2 + 2

---

---