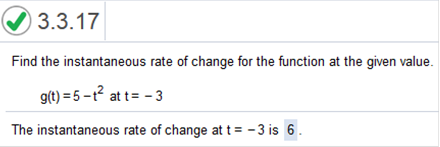Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel

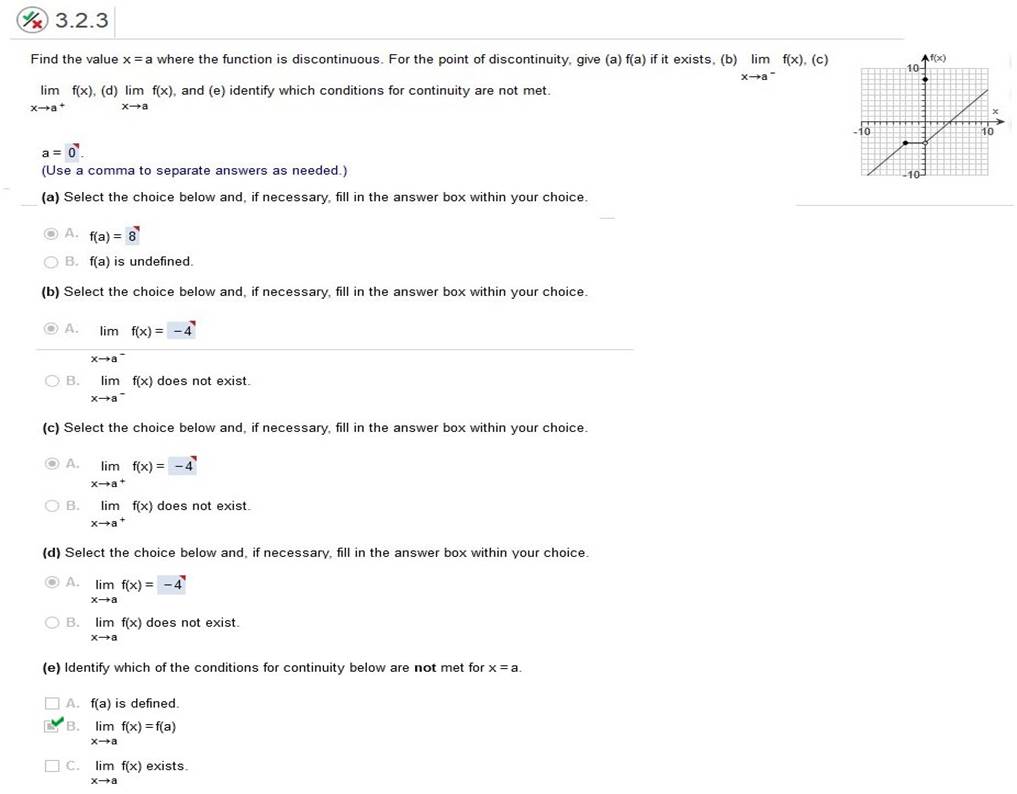
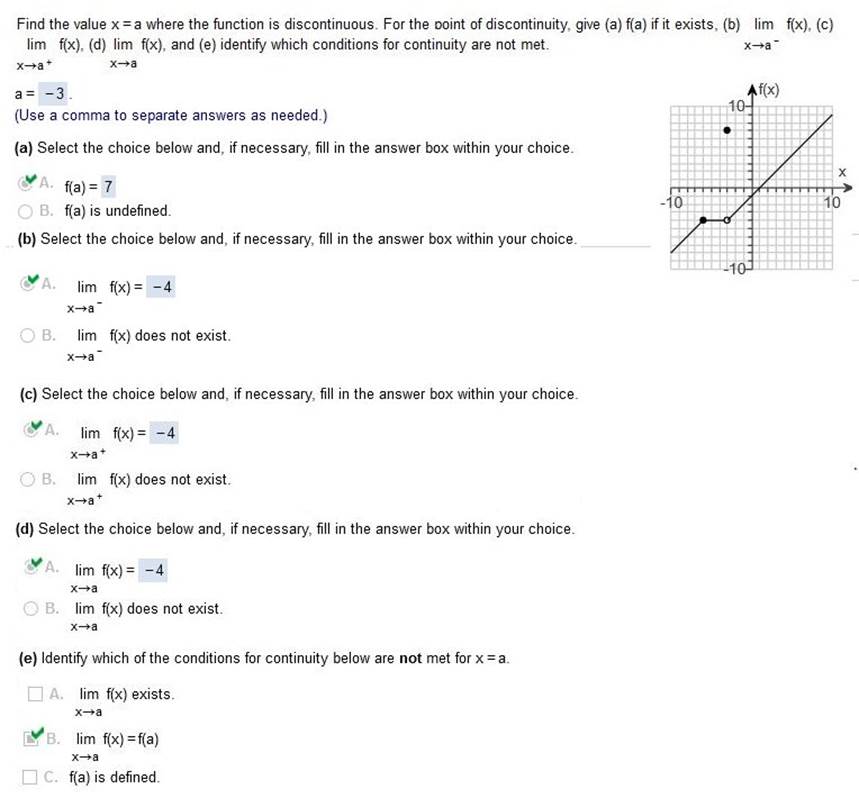
Find the value x = a where the function is discontinuous. For the point of​ discontinuity, give​ (a) f(a) if it​ exists,
(b) lim x-> a^- f(x), (c) lim x-> a⁺  f(x), (d) lim x-> a f(x) and (e) identify which conditions for continuity are not met
 
(a)    “Hollow circle” (hole in graph) use line f(x) point is “right or left” of f(x)
(b)   “Bottom Solid Circle” Use line x “above or below” line x

Study my answers and how they match the graph...
  Find the value x = a where the function is discontinuous. For the point of​ discontinuity, give​ (a) f(a) if it​ exists,
(b) lim x-> a^- f(x), (c) lim x-> a⁺  f(x), (d) lim x-> a f(x) and (e) identify which conditions for continuity are not met

Study my answers and how they match the graph...
  (a) Graph the given​ function, ​(b) find all values of x where the function is​ discontinuous, and ​(c)
find the limit from the left and the right at any values of x where the function is discontinuous.
a… Graph top to open circle (x)
b… the function is discontinuous at a point where it stops at an open circle
c… limit left is y and limit right is x. 

Study my answers and how they match the graph...
 
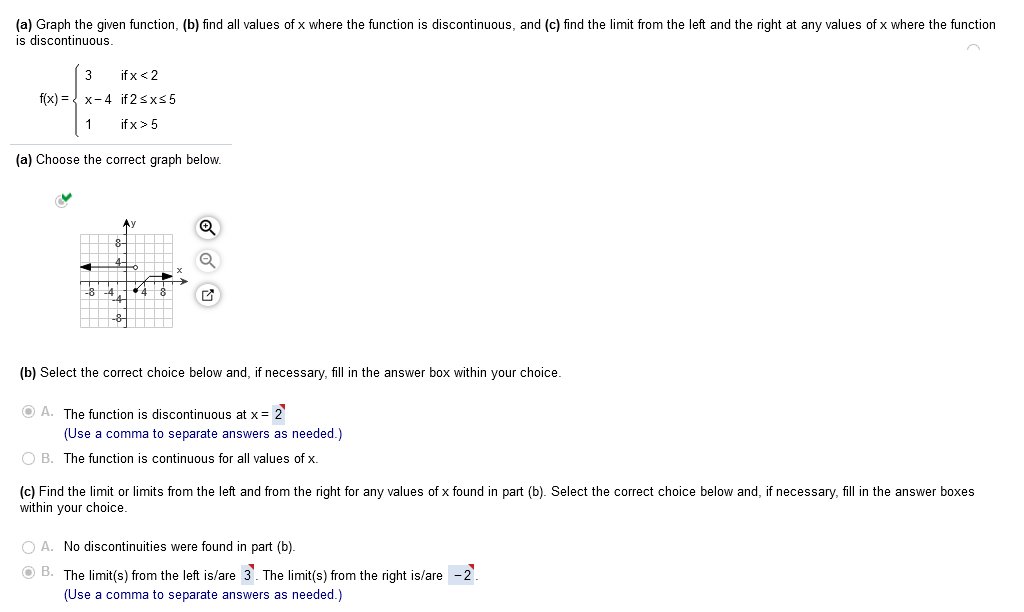
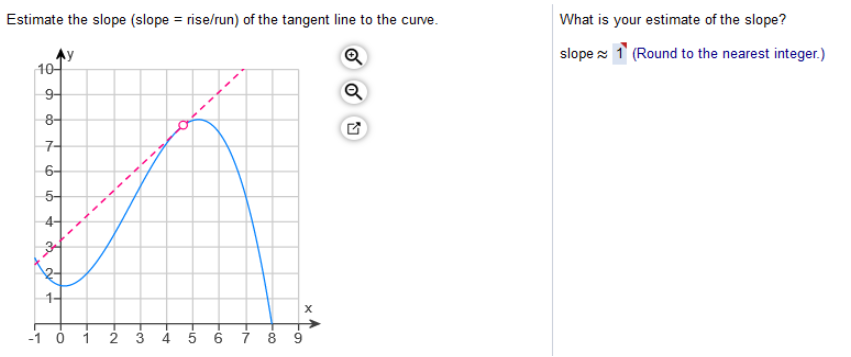
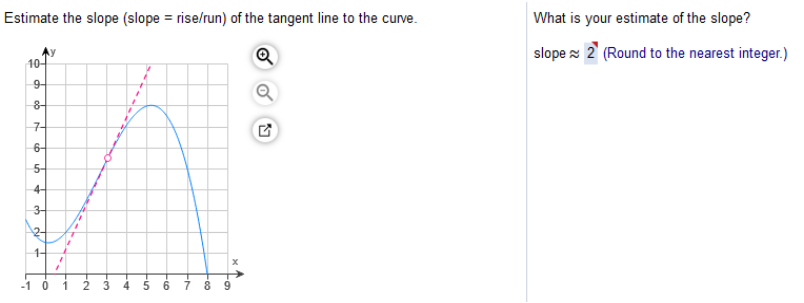
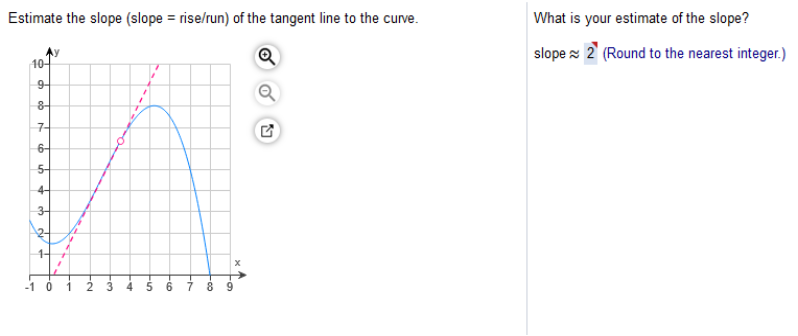
(a) Graph the given​  function
(b) find all values of x where the function is​ discontinuous
​(c) find the limit from the left and the right at any values of x where the function is discontinuous.

   
a… Graph top to open circle (x)
b… the function is discontinuous at a point where it stops at an open circle
c… limit left is y and limit right is x.
 
(a) Graph the given​ function
(b) find all values of x where the function is​ discontinuous
(c) find the limit from the left and the right at any values of x where the function is discontinuous.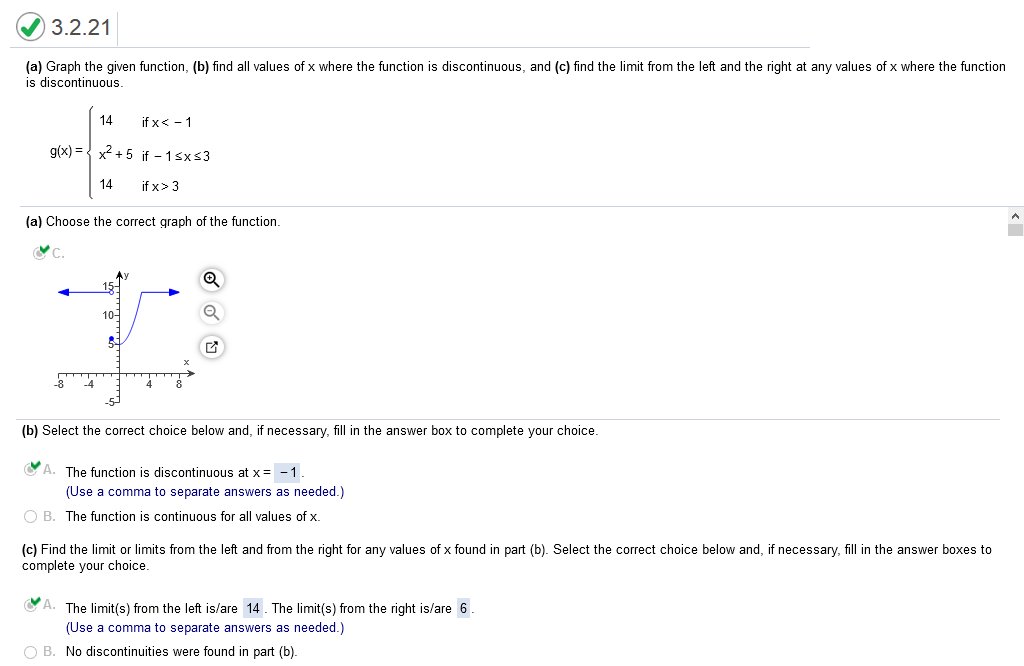
 

Consider the three parts of the rule of g. Each part can be graphed by plotting points in the appropriate interval.
Pay close attention to the open and closed circles on the graph sections.
Closed circles should be used with ≤ and ≥ =.
Open circles should be used with < and >
   
a… Graph the given​ function
b… find all values of x where the function is​ discontinuous, and ​
c… find the limit from the left and the right at any values of x where the function is discontinuous.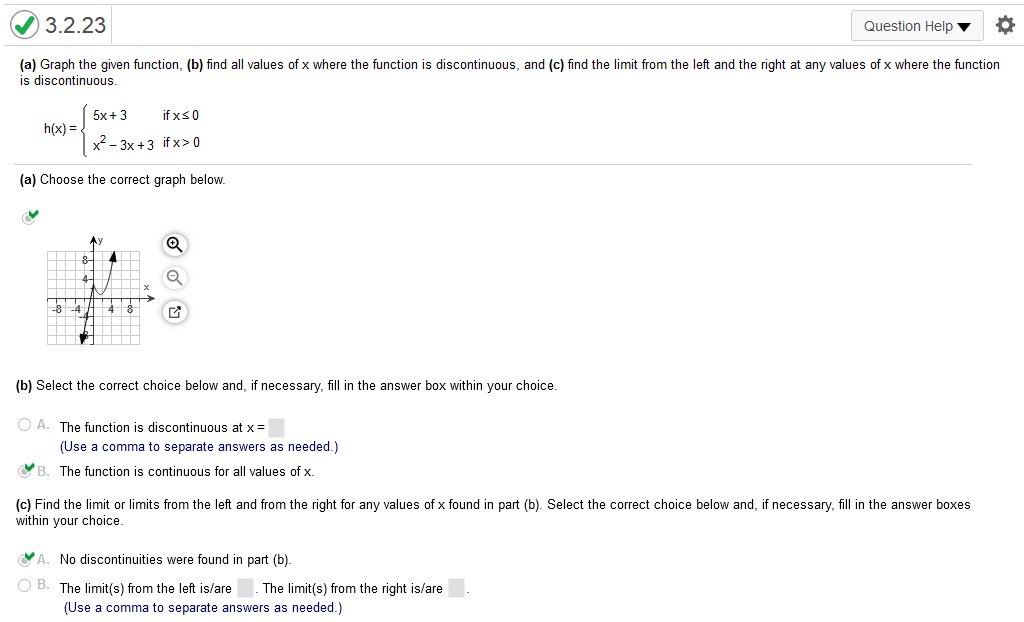
 
Estimate the slope​ (slope =​ rise/run) of the tangent line to the curve.

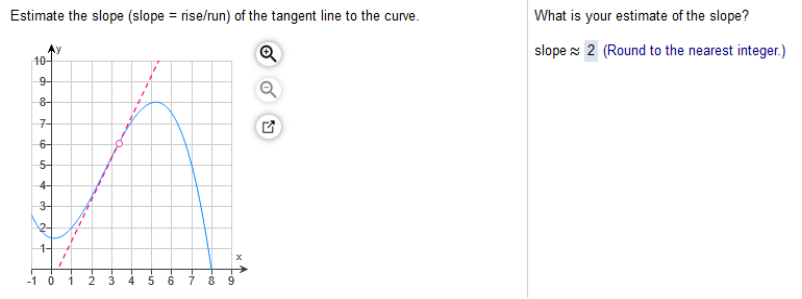Study my answers and how they match the graph...
   
Estimate the slope of the tangent line to the curve at the given point​ (x,y)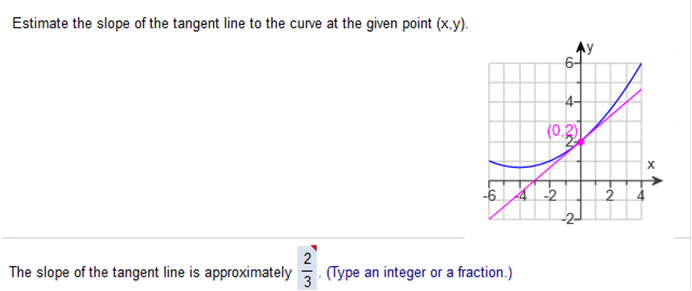

 
y - y₀ / x - x₀
(x₀, y₀) = (0, 2)
(x, y) ≈ (3, 4)
 
4 – 2 ÷ 3 – 0
= 2/3
   Estimate the slope of the tangent line to the curve at the given point (x,y).

(x₀, y₀) = (-1,2)
(x, y) ≈ (2,3)
3 – 2 / 2 – (-1) = 1/3
 
(x₀, y₀) = (-3,1)
(x, y) ≈ (3,4)
4 – 1 / 3 – (-3) = 3/6 = ½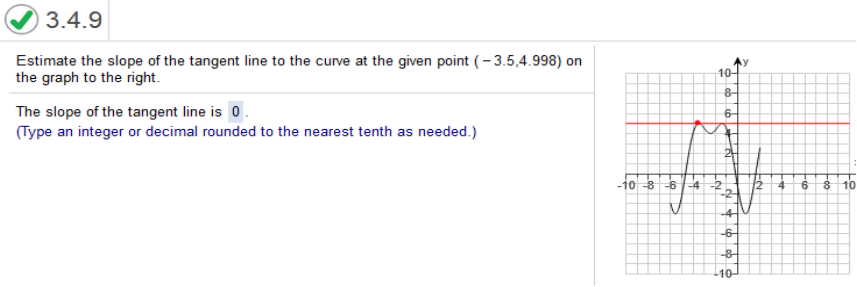
  Estimate the slope of the tangent line to the curve at the given point (-3.5, 4.998) on the graph to the right.

Study my answers and how they match the graph...
   
Find the​ x-value(s) where the graph does not have a derivative.
The​ x-value(s) where the function does not have a derivative​ is/are x​ = 1
​(Use a comma to separate answers as​ needed.)
 
A function f will not have a derivative if f is​ discontinuous, has a sharp point or​ corner, or has a vertical tangent at x.
Find the​ x-value(s) where the graph does not have a derivative.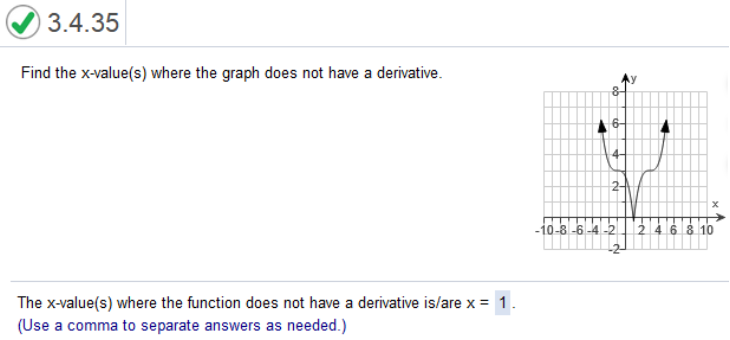

Study my answers and how they match the graph...
   
List the points in the graph in the interval 2 < x < 8 at which the function is not differentiable.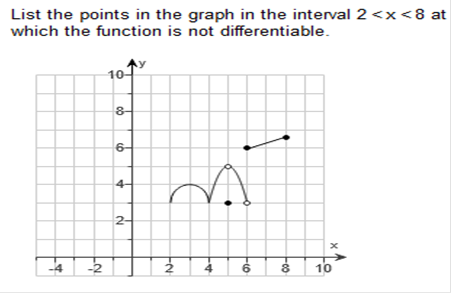

A function f will not have a derivative if f is​ discontinuous, has a sharp point or​ corner, or has a vertical tangent at x
The function f is discontinuous at x = 5 and x = 6 since the graph has holes at these points
Since the function is discontinuous at the points x = 5 and x = 6​, it follows that the function is not differentiable at x = 5 and x = 6
There is a third point x = 4 where the graph has a sharp corner and f fails to have a derivative
Therefore, in the interval 2 < x < 8​, f fails to have a derivative at x = 4​, x = 5, and x = 6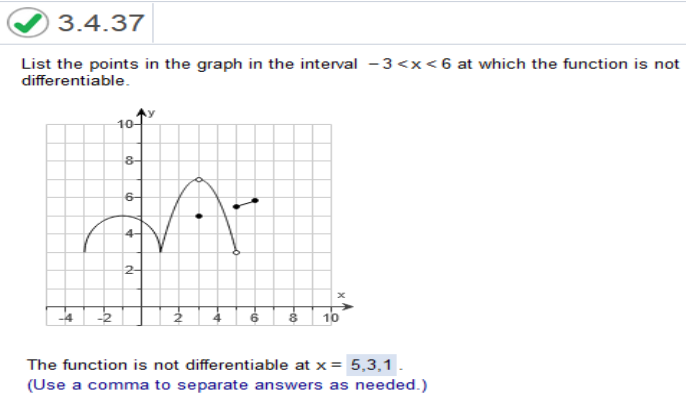
 
Study my answers and how they match the graph...
  Suppose the position of an object moving in a straight line is given by s(t) = 4t² + 3t + 3
Find the instantaneous velocity when t = 4
 
The instantaneous velocity at x = 4 is     35
 

Find derivative of 4t² + 3t + 3
The derivative of 4t² + 3t + 3 = 8t + 3
plug in the value of x = 4
8(4) + 3 = 35
  Find the instantaneous rate of change for the function at the given value
F(x) = x² + 2x at x = 0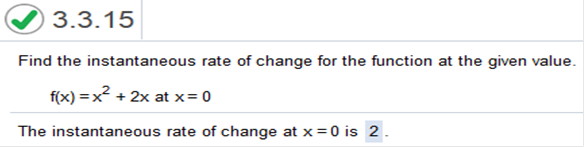
 

 
Find derivative of x² + 2x at x) =            2x + 2
plug in the value of x = 0
2(0) + 2 = 2
The instantaneous rate of change a is 2
  Find the instantaneous rate of change for the function at the given value.

Find the derivative of -t² + 5 =   -2t
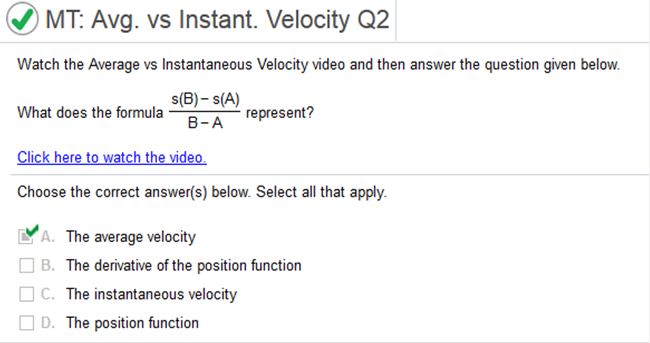
Plug in t = -3
-2 x -3 = 6  
Explain the difference between the average rate of change of y as x changes from a to b,
and the instantaneous rate of change of y at x = a

 
Please focus and study the answer to get the hang of this.
   
Suppose that the total profit in hundreds of dollars from selling x items is given by P(x) = 5x² -7x + 7
Complete parts a through d below.

Find the average rate of change of profit as x changes from 3 to 5
F(b) – f(a) / b – a
5(3)² – 7(3) + 7 = 31
5(5)² – 7(5) + 7 = 97
97 – 31 / 5 – 3 = 33(100) = 3,300
average rate of change of profit as x changes from 5 – 7 is 3,300
 
Find the average rate of change of profit as x changes from 3 to 4
5(3)² – 7(3) + 7 = 31
5(4)² – 7(4) + 7 = 59
59 – 31 / 4 – 3 = 28(100) = 2,800
average rate of change of profit as x changes from 5 – 7 is 2,800
 
Find and interpret the instantaneous rate of change of profit with respect to the number of items produced when x = 3.
​(This number is called the marginal profit at x = 3​.)
Find derivative of 5x² -7x + 7 = 12x – 7
Plug in the value of x
10(3) – 7 = 23(100) = 2,300
  Select the function f(x) = x² and set the value of x at 1.
Decrease the value of h by using the​ "slide" button for h.
Estimate the instantaneous rate of change of f at x = 1.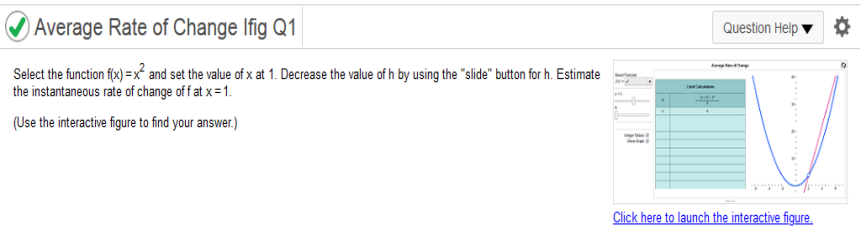
.
This is very simple. If you are asked to do this, simply follow directions.
   
Select the function f(x) = x³ and set the value of x at 1. Decrease the value of h by using the​ "slide" button for h.
Estimate the instantaneous rate of change of f at x = 0.
 
 

This is very simple. If you are asked to do this, simply follow directions.
   
Watch the Average vs. Instantaneous Velocity video and then answer the question given below.
Is the following statement true or​ false?
If​ Pete's average velocity was calculated while skiing at a constant rate between two​ flags,
this would match the instantaneous velocity at the
instant he passed the midway point between the flags.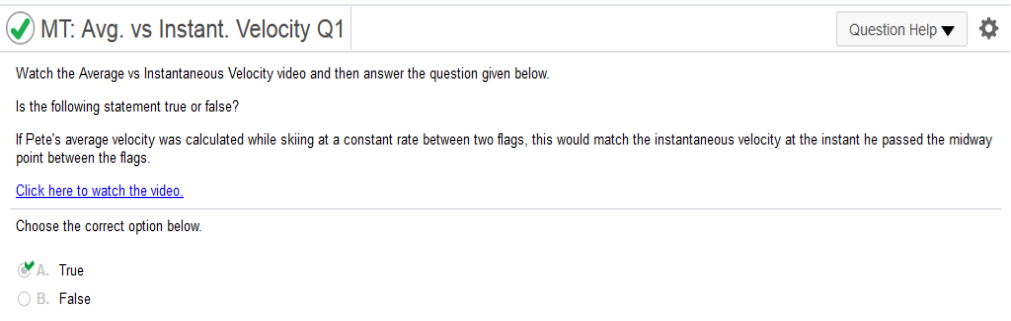 

This is very simple. If you are asked to do this, simply follow directions.
   
Watch the Average vs. Instantaneous Velocity video and then answer the question given below.
What does the formula  represent?

 

This is very simple. If you are asked to do this, simply follow directions.
 
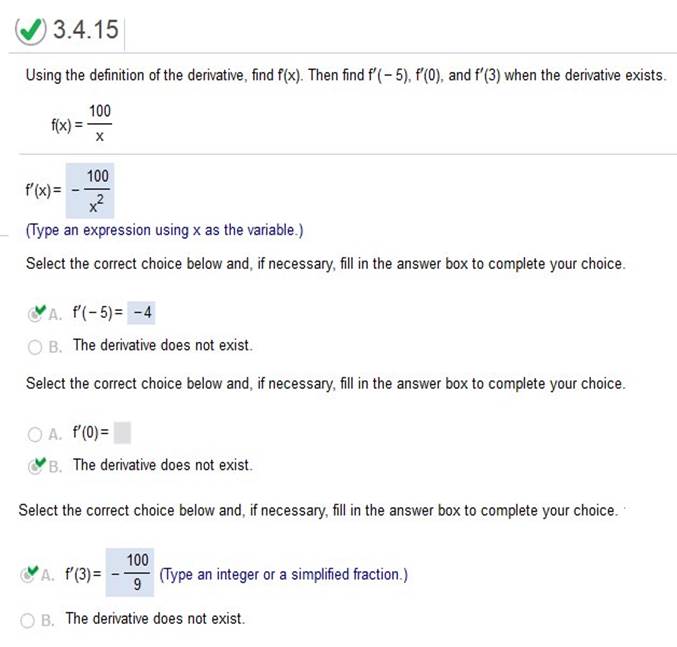
Using the definition of the​ derivative, find f’(x), then f’(1), f’(2), f’(3) when the derivative exists
f(x) = -x² +5x – 4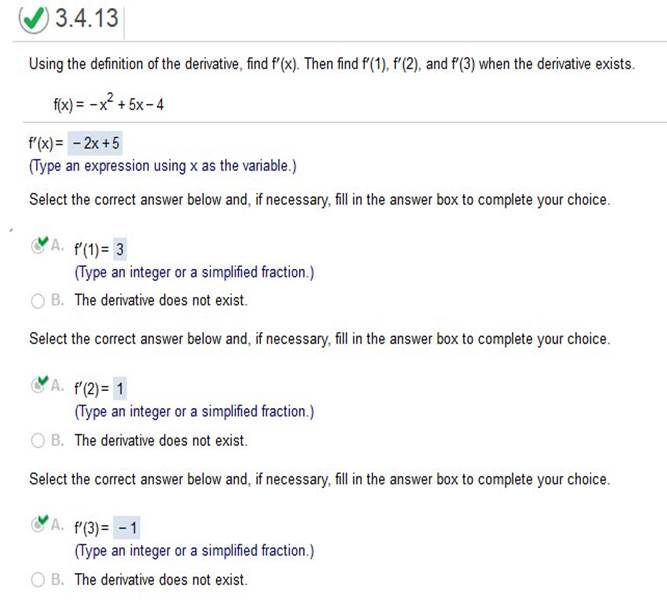
 

 
Find derivative of -x² +5x – 4 =          -2x + 5
then plug in f (1), (2), (3)
 
-2(1) + 5 = -2 + 5 =        3
-2(2) + 5 = -4 + 5 =        1
-2(3) + 5 = -6 + 5 =       -1
   
Using the definition of the​ derivative, find​ f'(x) then find f’(-5), 0, 3 when the derivative exists

            f(x) =

 

Find derivative of 100 / x =        -100 / x²
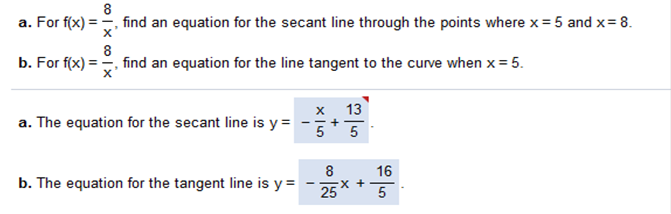
Then plug in -5, 0, 3
Does not exist at/for 0
   
For the given​ function, find
​(a)… the equation of the secant line through the points where x has the given values and
​(b)… the equation of the tangent line when x has the first value
y = f(x) = x² + x, x = 3, x = 6
 
Answer: 7x – 9
 
f(b) – f(a) / b – a
42 – 12 / 6 – 3 = 10
(3,12) (6,42)
y – y₁ = m (x – x1)
y – 12 = 10(x – 3)
y = 10x - 30 + 12
The equation of the secant line is: y = 10x – 18
 
https://www.wolframalpha.com/widgets/view.jsp?id=9173f9cc16d0c7e07f39309621d40515
  For f(x) = 8/x, find an equation for the secant line through the points where x = 5 and x = 8
For f(x) = 8/x find an equation for the line tangent to the curve when x = 5.

8/x
f(b) – f(a) / b - a
Let a = 5 and b = 8
f(a) = 8/5
f(b) = 1
1 – 8/5 / 8 – 5 =
-3/5 / 3 =         -1/5
y – y1 = m (x – x1)
y – 1 = -1/5(x – 8)
y = -1/5(x) -1/5 ( – 8) + 1
y = -x/5 + 8/5 + 1
 
The equation for the secant line is y = -x/5 + 13/5
For f(x) = 8/x find an equation for the line tangent to the curve when x = 5
https://www.wolframalpha.com/widgets/view.jsp?id=9173f9cc16d0c7e07f39309621d40515
 
The equation for the tangent line is y = -8/25x + 16/5
 
Let a = 5 and b = 7
f(a) = 7/5
f(b) = 1
1 – 7/5 / 7 – 5 =
-3/5 / 3 =
-1/5
y – y1 = m (x – x1)
y – 1 = -1/5(x – 7)
y = -1/5(x) -1/5 (–7) + 1
y = -x/5 + 12/5
  Suppose the demand for a certain item is given by ​D(p) = -2p² - 3p + 500​, where p represents the price of the item in dollars.
a. Find the rate of change of demand with respect to price.
b. Find and interpret the rate of change of demand when the price is ​$8.
 
Find the derivative of -2p² - 3p + 500 =
-4p - 3
 
When the price is $8 demand is decreasing at a rate of 35 items for each increase of $1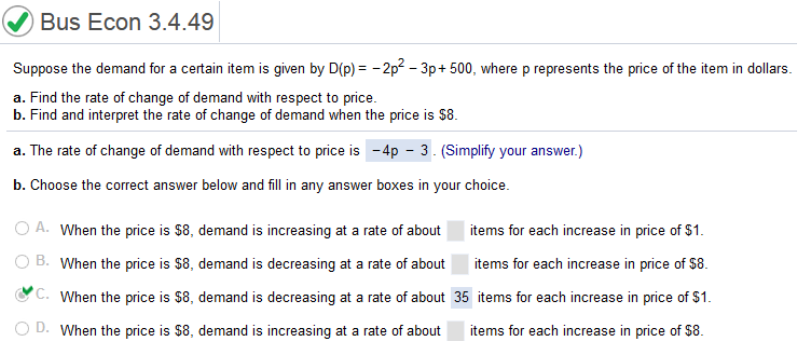

 
Plug the value of 8 in
-4(8) – 3 = -35

---

---