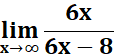|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Homework Chapter
1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM Need A Tutor? Need Homework Help?
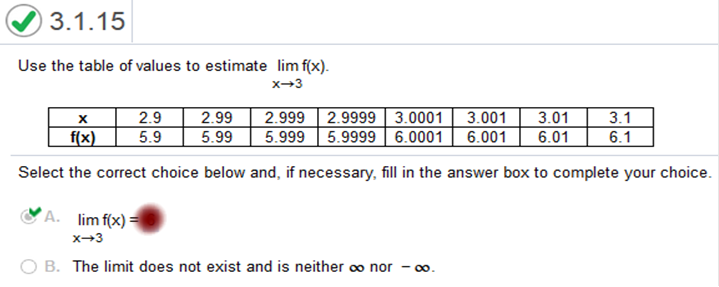
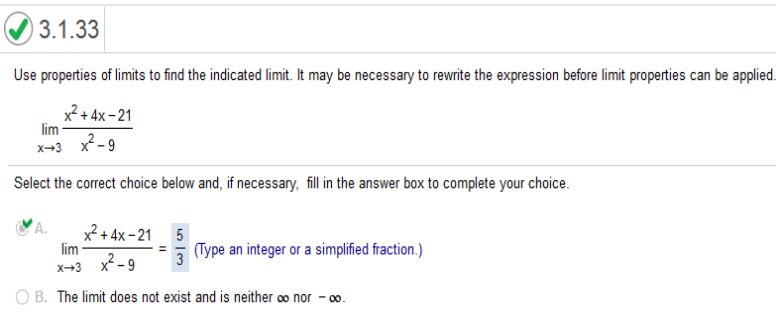
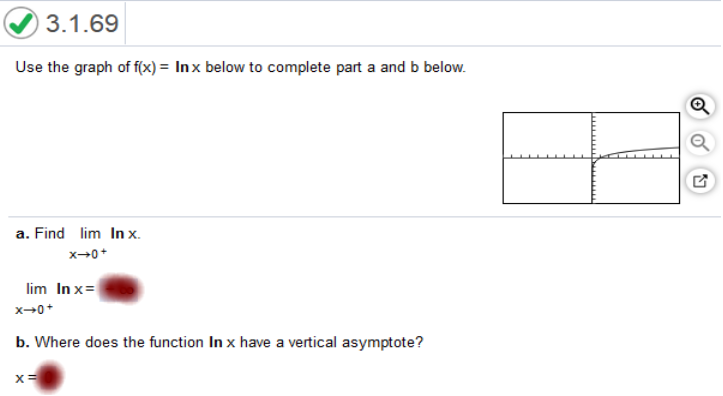
Calculus For Business Homework Chapter 2 Part A Use the table of values to estimate:
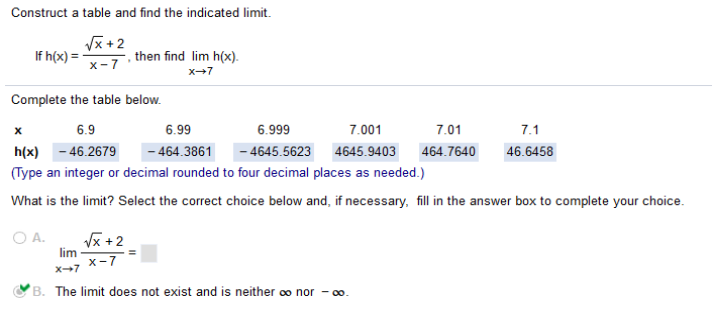
Construct a table and find the indicated limit. If h(x) =
Plug the values in and solve. Compute each separately. For example: √6.9 +(2) / 6.9 – 7 = -46.2679 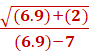 = -46.2679 = -46.2679
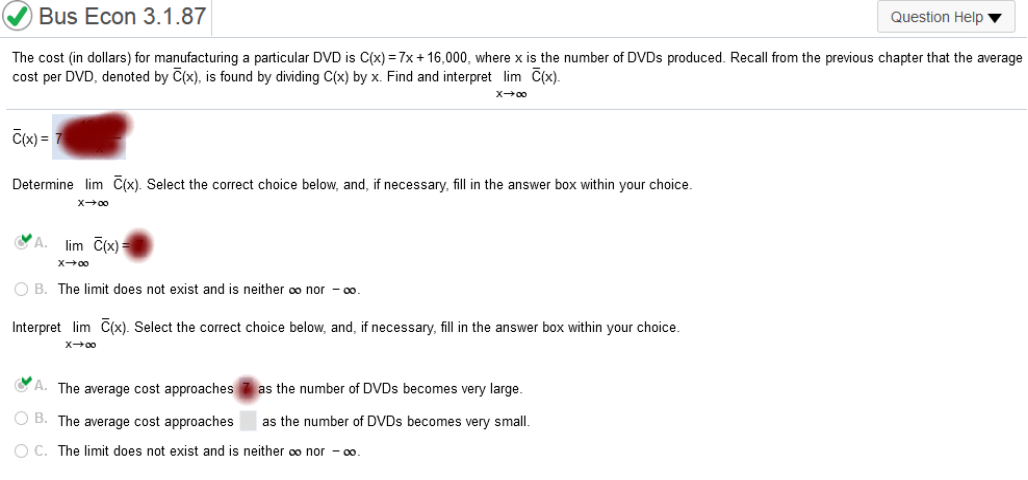
Recall from the previous chapter that the average cost per DVD, denoted by Find and interpret
Now we plug in the value So, we are left with 7 The cost (in dollars) for manufacturing a particular DVD is C(x) = 4x + 15,000, where x is the number of DVDs produced. Recall from the previous chapter that the average cost per DVD, denoted by Find and interpret
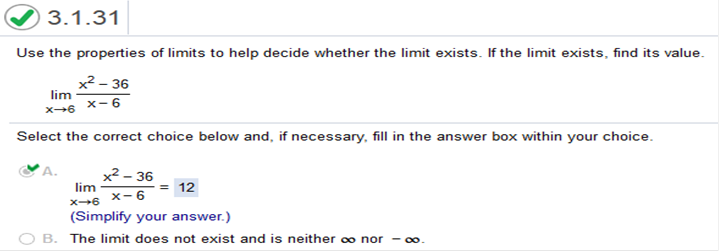
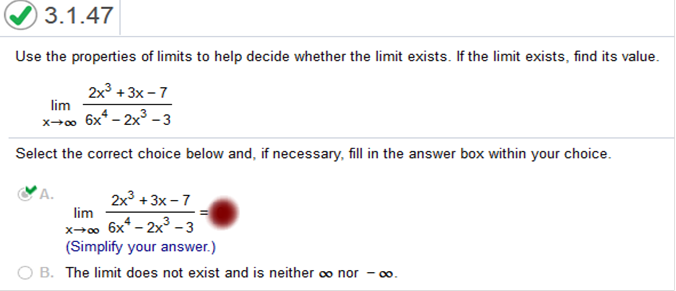
This problem is the same steps as above! Use the properties of limits to help decide whether the limit exists. If the limit exists, find its value.
Then we plug in the value 6. We can find the derivative of the numerator and denominator separately. The formula for finding a derivative is nn – 1 with “n” being the exponent. So, what we do is multiply the value of the exponent by the number in front of it and subtract 1 from the exponent. For instance, if we have x2 and need to find the derivative we multiply 2 (which is the exponent) by 1, and subtract 1 from the exponent. So, it would be 2(1)2 – 1. The derivative of x2 is 2x. If a number value has no exponent, then the derivative of that number is 0. For instance, the derivative of 1 = 0, 2 = 0, 3 = 0, and so on. The derivative of x2 – 36 = 2x The derivative of x – 6 = 0 We are left with 2x. Now we plug in the value 6. 2(6) = 12 Use properties of limits to find the indicated limit. It may be necessary to rewrite the expression before limit properties can be applied.
Find the derivative and plug in the value of 3. The derivative of the limit is in fraction form: 2x + 4 / 2x 2x + 4 / 2x We plug in the values. 2(3) + 4 / 2(3) = 10 / 6 Now we reduce to the fraction Use the properties of limits to help decide whether the limit exists. If the limit exists, find its value.
Find the derivative and plug in the value of 6. I can do this in my head because I have done so many like this. So, you can practice this on paper. Use the properties of limits to help decide whether the limit exists. If the limit exists, find its value.
This is similar, however, all we need to do is find the derivative of After finding the derivative, we are left with x / x Use the properties of limits to help decide whether the limit exists. If the limit exists, find its value.
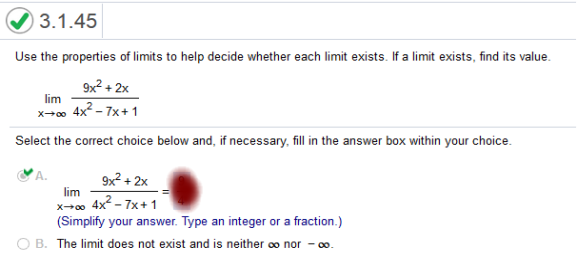
This is a little trick so I will break the problem down. We need to find the derivative of First, we find the derivative of 9x2 + 2x = 18x + 2 Next, we find the derivative of 4x2 – 7x + 1 = 8x – 7 So, we are left with a fraction Since we will be plugging in the value discounted from the rest of the values in the fraction, and the right side will be cancelled out. So, we will have So, we simplify the fraction to 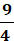
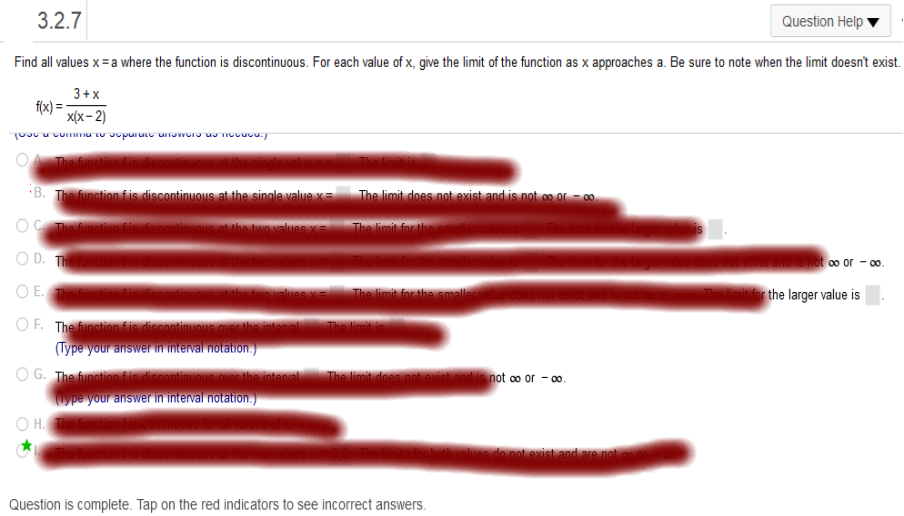
If you don’t understand any of this, please contact me. I will take the time to explain. 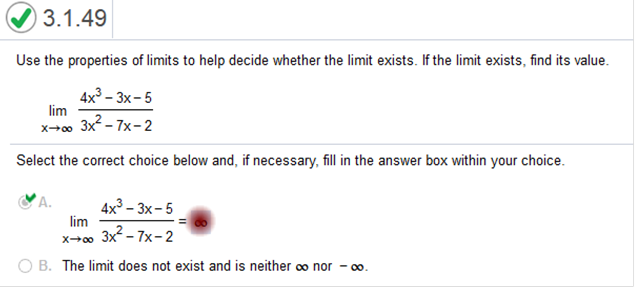 This is the same as above. If you don’t understand any of this, please contact me. I will take the time to explain. Find all values x = a where the function is discontinuous. For each value of x, give the limit of the function as x approaches. a. Be sure to note when the limit doesn't exist.
(example x --> 3), then f(x) is discontinuous (or vanishes). In this case, it vanishes at 0, 2 Naturally, the limits do not exist for either value, as well, because the limit is not approaching any value and vanishes. Find all values x = a where the function is discontinuous. For each value of x, give the limit of the function as x approaches a. Be sure to note when the limit doesn't exist. F(x) = 2x2 + 3x -3 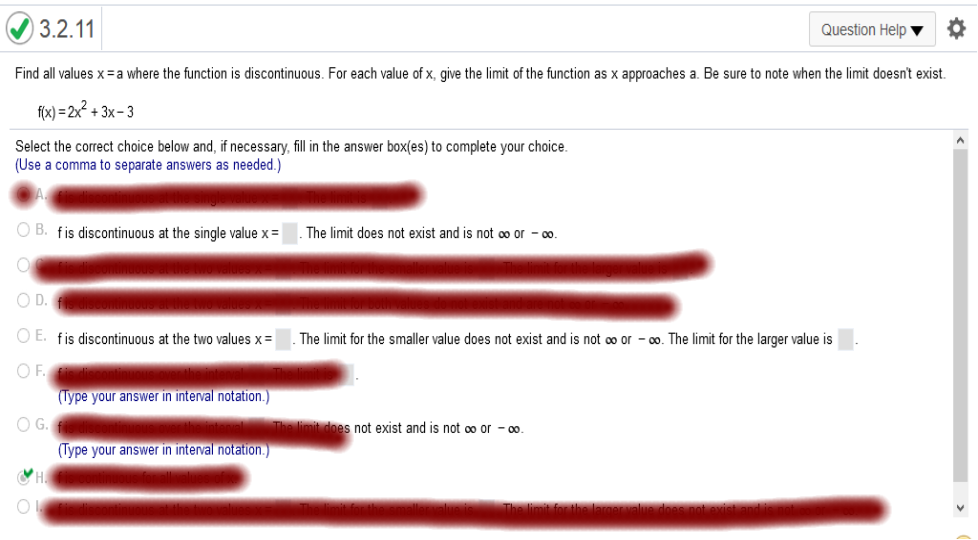
Explanation Solve 2x2 + 3x = -3 for x x = -1, and -1/2 Solve the limit for x = -4 for both. When both limits = the same, then f is continuous The cost to transport a mobile home depends on the distance, x, in miles that the home is moved. Let C(x) represent the cost to move a mobile home x miles. One firm charges as follows. 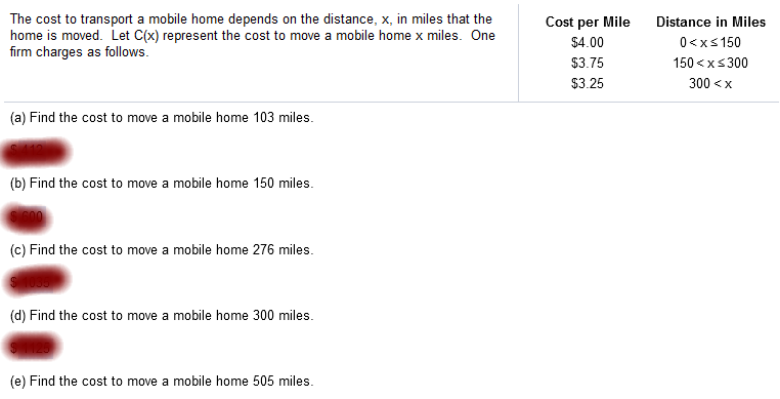 
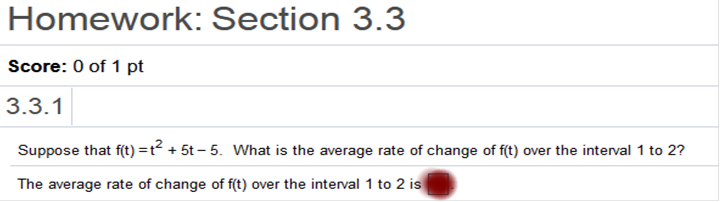
A. Falls in between 0 – 150 miles so the cost is $4 per mile, and we multiply 103 by 4.00 = 412 B. Falls in between 0 – 150 miles so the cost is $4 per mile, and we multiply 150 by 4.00 = 600 And so on… What is the average rate of change of f(t) over the interval 1 to 2 The average rate of change of f(t) over the interval 1 to 2 is ___
f(b) – f(a) / b – a f(t) = t2 + 5t – 5 f(1) = (1)2 + 5(1) – 5 f(1) = 1 + 5 – 5 = 1 f(2) = (2)2 + 5(2) – 5 f(2) = 4 + 10 – 5 = 9 f(b) – f(a) / b – a 9 – 1/ 2 - 1 = 8 The average rate of change of f(t) over the interval 1 to 2 is 8 Check https://www.emathhelp.net/calculators/calculus-1/average-rate-of-change-calculator/ 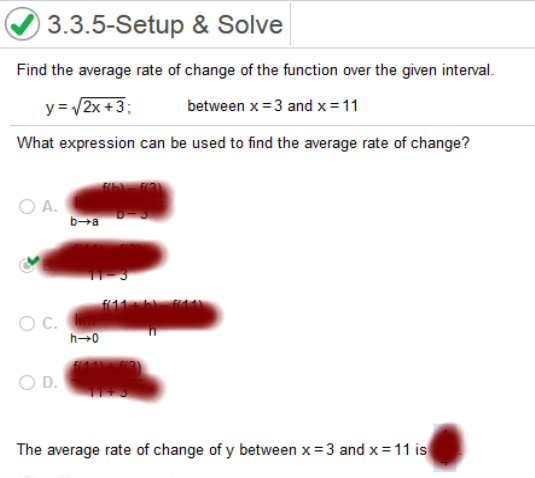
Find the average rate of change of the function over the given interval. y = √2x + 3 between x = 3 and x = 11 f(b) – f(a) / b – a f(3) = √2(3) + 3 = √6 + 3 = √9 = 3 f(3) = √2(11) + 3 = √22 + 3 = √25 = 5 f(b) – f(a) / b – a 5 – 3 / 11 - 3 = Find the average rate of change of the function over the given intervals f(x) = 7x3 + 7; a) [2, 4], b) [=3, 3] 
We simply plug in the values, subtract (larger from smaller, and divide by the larger value of the set minus the smaller value. a) 7(4)3 + 7 – 7(2)3+ 7 / 4 – 2 = 455 – 63 / 2 = 392 / 2 = 196 The next one is tricky. Watch carefully how I factor the values. b) 7(3)3 + 7 – 7(-3)3 + 7 / 3 – (-3) = 196 – (-182) / 6 = 378 / 6 = 63 Find the average rate of change for the function over the given interval. y= ex between x = -4 and x = -2 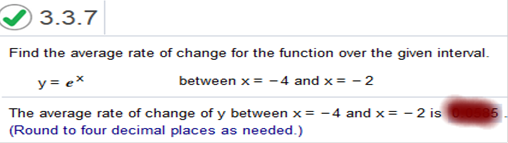
x = -4 x = -2 e = 2.71828 a = 2.71828-4 = .0183 b = 2.71828-2 = .1353 f(b) – f(a) / b – a .1353 - .0183 / -2 – (-4) = .1353 - .0183 / -2 + 4 .117 / 2 = 0.0585 Check https://www.emathhelp.net/calculators/calculus-1/average-rate-of-change-calculator/ Suppose the position of an object moving in a straight line is given by s(t) = 5t2 + 3t + 5. Find the instantaneous velocity when t = 4. What expression can be used to find the instantaneous velocity at the given time? The instantaneous velocity at t = 4 is 43 
Part 1: the limit definition of derivative is And we are given the value of x, so we simply plug in the value of x and replace f with s because we are given the The formula for the straight line at “s(t)” = 5t2 + 3t + 5 Part 2: is a lot easier. We already covered the steps to finding the derivative of a function. So, we need to find the derivative of s(t) = 5t2 + 3t + 5 and plug in the value of t = 4. Remember the derivative of 5t2 is 5(2)t2 – 1 = 10t 3t is 1(3)1 – 1 = 3 The derivative of a number without a variable or exponent is 0 So, we are left with 10t + 3 Now we plug in the value 4 10(4) + 3 = 40 + 3 = 43 What is the value of the limit?
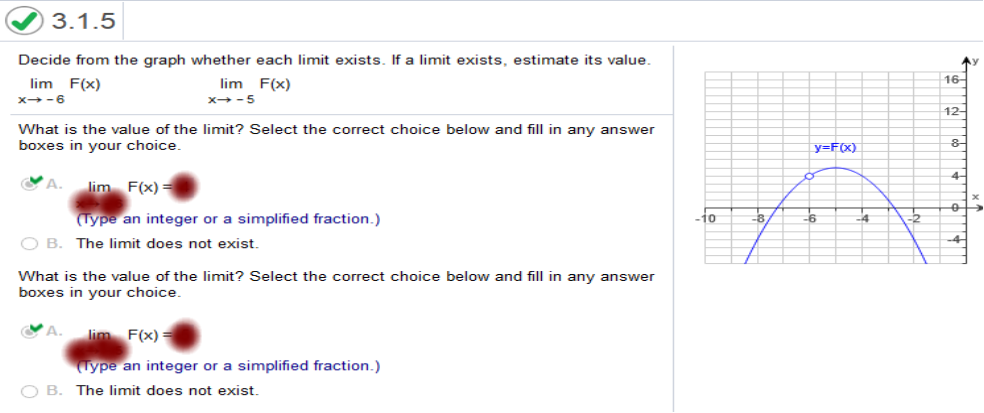
We are given x->-6 and the limit meets on the graph at positive 4 We are given x->-5 and the limit meets on the graph at positive 5 Find
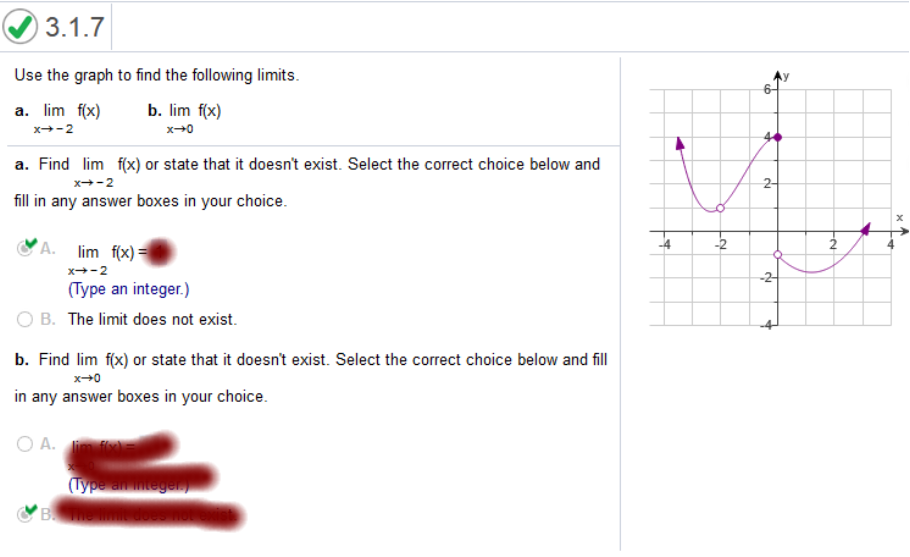
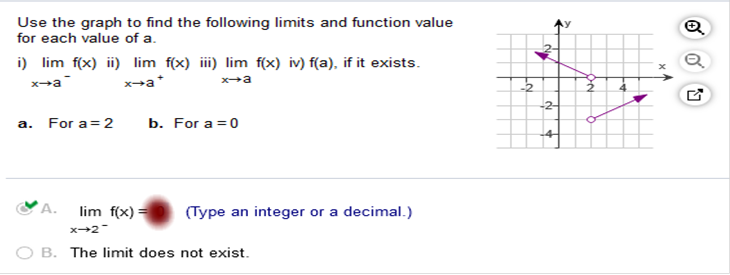
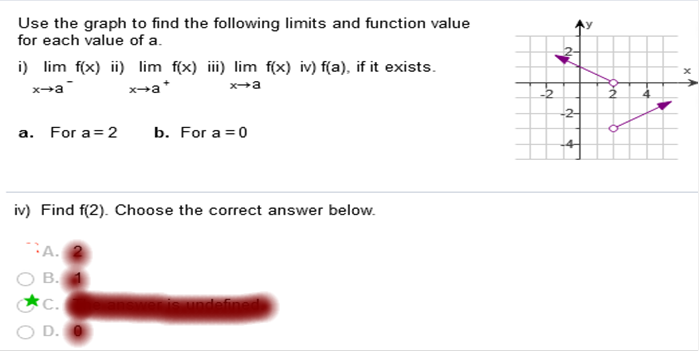
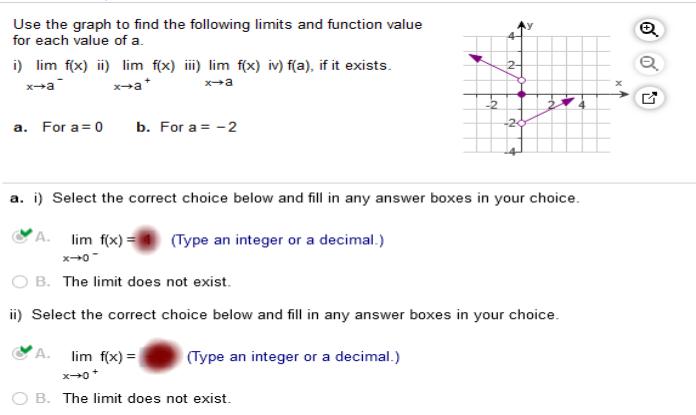
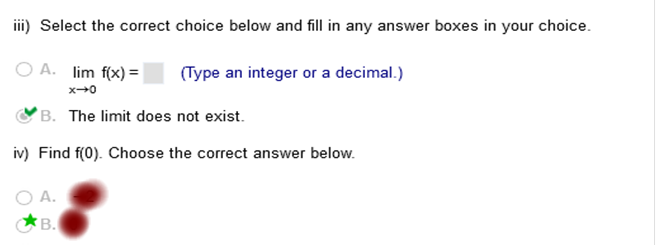
We are given x-> -2 and the limit meets on the graph at +1 We are given x-> 0 and the limit does not meet. It vanishes, therefore the limit does not exist Use the graph to find the following limits and function value for each value of a.
Study my answers and how they match the graph... Use the graph to find the following limits and function value for each of the value of a.

Study my answers and how they match the graph... Refer to the figure below to find the limit lim f(x). What is the limit 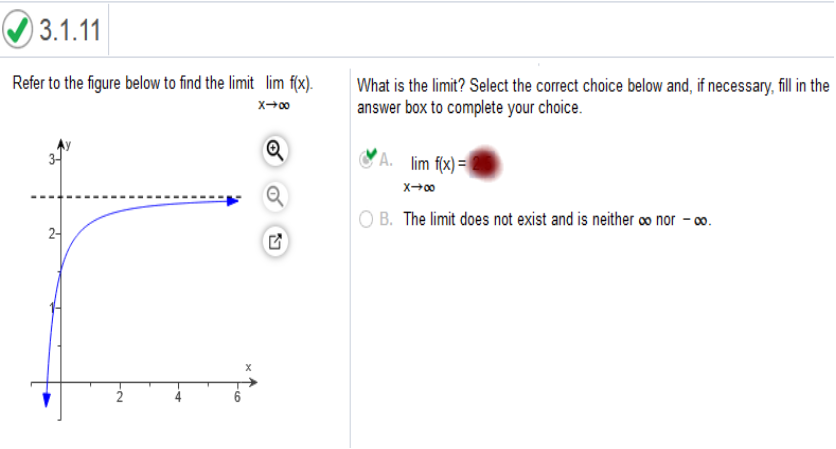
Study my answers and how they match the graph... 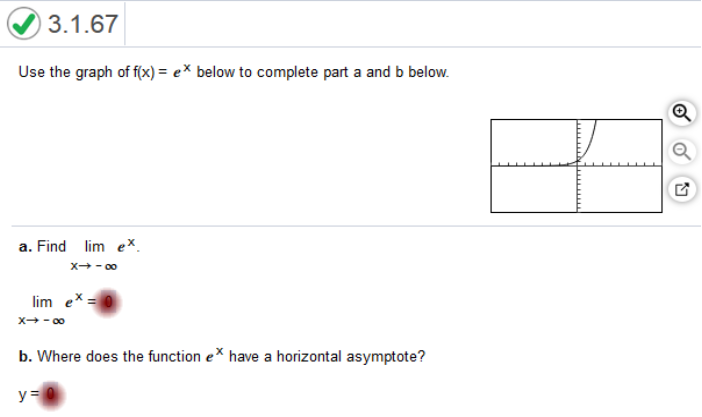
Study my answers and how they match the graph...
Homework Chapter
1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM Need A Tutor? Need Homework Help?
|
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |