|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Homework Chapter
1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM Need A Tutor? Need Homework Help?
Calculus For Business Homework Chapter 1 Part B Fixed cost is $200; 20 items cost $600 to produce. 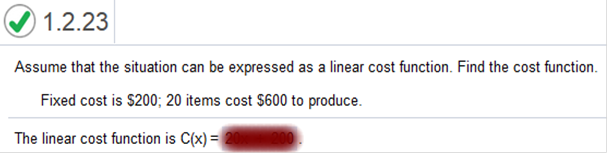
C(x) = mx + b 600 = m (20) + 200 Subtract 200 for both sides 400 = m(20) Divide both sides by 20 M = 20 C(x) = 20x + 200 Assume that the situation can be expressed as a linear cost function. Find the cost function in this case. Marginal cost: $40; 170 items cost $9000 to produce. 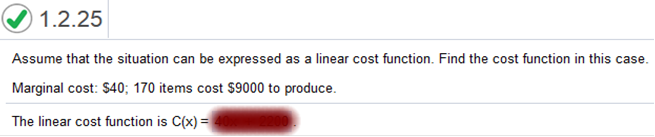
The linear cost function is C(x)= 40x + 2200 C(x) – 9000 = 40(x – 170) C(x) – 9000 = 40x – 6800 (add 9000 to each side) C(x) = C(x) = 40x + 2200 To produce x units of a religious medal costs C(x) = 12x + 33. The revenue R(x) = 23x. Both cost and revenue are in dollars. a. Find the break-even quantity. b. Find the profit from 370 units. c. Find the number of units that must be produced for a profit of $110 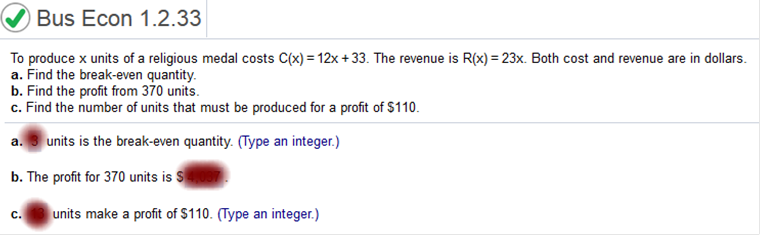
3 units is the break-even quantity. 23x = 12x + 33 (subtract 12x from both sides) 11x = 33 divide both sides by 11 x = 3 b. Find the profit from 370 units. P (x) = 23x – (12x + 33) remove the parentheses and perform the subtraction in the right side P (x) = 11x – 33 (substitute 370 for x in the equation above) P (370) = 11(370) – 33 = P (370) = $4,037 Profits units for 370 units is $4,037. c. Find the number of units that must be produced for a profit of $110 110 = 11x – 33 (add 33 to both sides) 143 = 11x (divide both sides by 11) 13 units make a profit of $110. Joanne sells silk-screened T-shirts at community festivals and craft fairs. Her marginal cost to produce one T-shirt is 2.50. Her total cost to produce 60 T-shirts is $240 and she sells them for $6 each. a. Find the linear cost function for Joanne's T-shirt production. b. How many T-shirts must she produce and sell in order to break even? c. How many T-shirts must she produce and sell to make a profit of $800? 
Find the linear cost function for Joanne's T-shirt production. Explanation C(X) = mx + b 240 = 2.50(60) + b = 240 = 150 + b (subtract 150 from both sides) 90 = b linear cost function is c(x) = 2.50x + 90 How many T-shirts must she produce and sell in order to break even Explanation P(x) = r(x) – c(x) 6x = 2.50x + 90 (subtract 2.50 from both sides) 3.50x = 90 (divide both sides by 3.50) x = 25.7 Joanne must produce and sell 26 t-shirts to break even. How many T-shirts must she produce and sell to make a profit of $800? Explanation 800 = 6x – (2.50x + 90) (subtract 2.50x from 6x) 800 = 3.50x – 90 (add 90 to both sides) 890 = 3.50x (divide 3.50 by both sides) 254.28 254.28 must be raised to 255 for Joanne to make a profit of $800 Joanne must produce 255 t-shirts to make a profit of $800. while the cost to produce 400 cups is $38.92. Assume the cost C(x) is a linear function of x, the number of cups produced. Answer parts a through f. Find a formula for C(x). Choose the correct answer below. 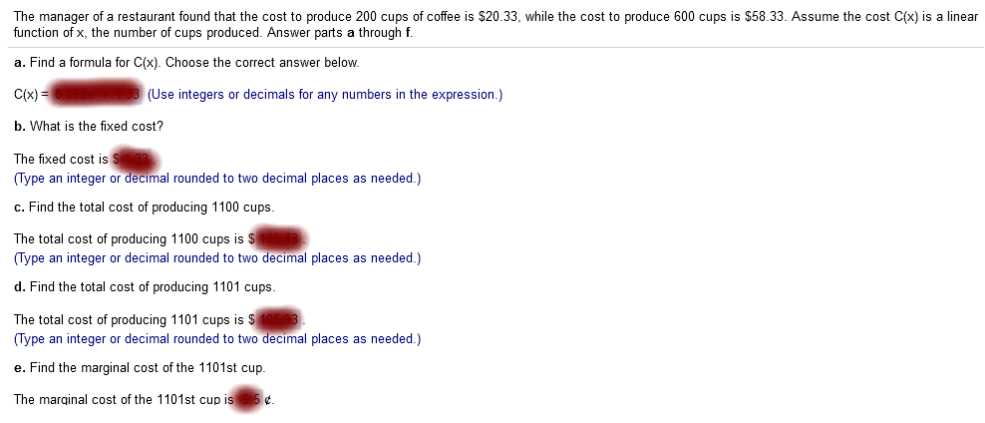 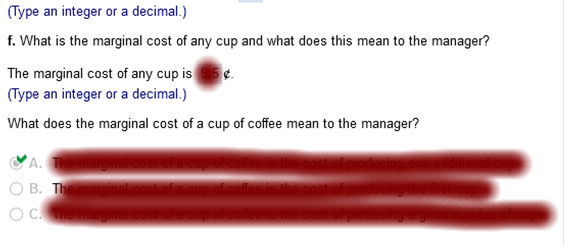
m = y2 – y1 / x2 – x1 (x1, y1) = (200, 20.12) (x2, y2) = (400, 38.92) 38.92 – 20.12 / 400 – 200 18.8 / 200 = .094 20.12 = .094(200) + b 20.12 = 18.8x + b (subtract 18.8 from both sides) 1.32 = b C(x) = 0.094x + 1.32 What is the fixed cost? b = fixed cost so $1.32 is the fixed cost The total cost of producing 1000 cups is $ C (1000) = 0.094(1000) + 1.32 C (1000) = 95.32 The total cost of producing 1000 cups is $95.32. The total cost of producing 1001 cups is $ C(1001) = 0.094(1001) + 1.32 C(1000) = 95.41 Find the marginal cost of the 1001st cup. 0.094 x 1000 = 9.4 9.4 cents What does the marginal cost of a cup of coffee mean to the manager? A. The marginal cost of a cup of coffee is the cost of producing one additional cup. B. The marginal cost of a cup of coffee is the cost of producing the first cup. C. The marginal cost of a cup of coffee is the cost of producing a given number of cups. R(x) = 300x. No more than 58 units can be sold. Find and analyze the break-even quantity, then find the profit function. R(x) = C(x) 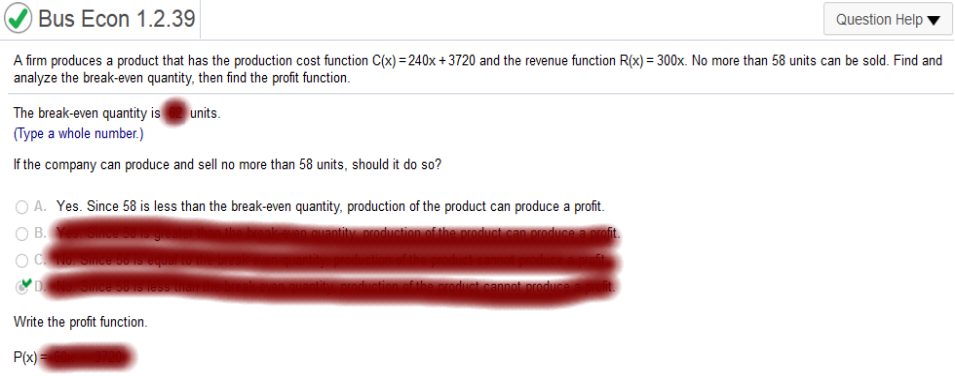
300x = 240x + 3720 (subtract 240x from both sides) 60x = 3720 (divide by 60) x = 62 The break-even quantity is 62 units. If the company can produce and sell no more than 58 units, should it do so? D. No. Since 58 is less than the break-even quantity, production of the product cannot produce a profit. Write the profit function. P(x) = R(X) – C(X) 300x – (240x + 3720) subtract 240x P(x) = 60x – 3720 A person is the manager of a firm. He is considering manufacturing a new product, so he asks the accounting department for cost estimates and the sales department for sales estimates. After he receives the data, he must decide whether to go ahead with production of the new product. Analyze the following data (find a break-even quantity) and then decide what the manager would do in this case. Also, write the profit function. C(x) = 160x + 1400 and R(x) = 140x 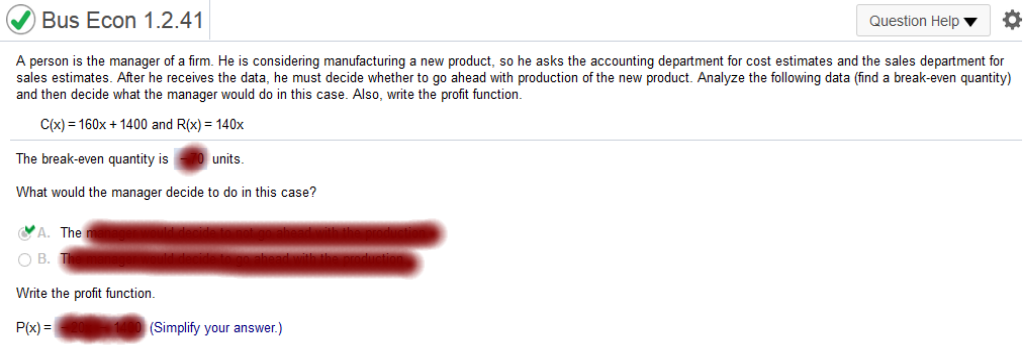
140x = 160x + 1,400 (subtract 160x) -20x = 1,400 (divide by -20) x = break even -70 What would the manager decide to do in this case? A. The manager would decide to not go ahead with the production. B. The manager would decide to go ahead with the production Write the profit function P(x) = R(x) - C(x) 140x – (160x + 1400) -20x – 1400 
Suppose that the fixed cost for a product is $260 and the break-even quantity is 65. Find the marginal profit (the slope of the linear profit function). The marginal profit is Margin profits = fixed costs / units sold Margin profits = 260 / 65 = 4 Suppose that the supply function for honey is p = S(q) = 0.3q + 2.7, where p is the price in dollars for an 8-oz container and q is the quantity in barrels. Suppose also that the equilibrium price is $4.50 and the demand is 2 barrels when the price is $6.70. Find an equation for the demand function, assuming it is linear. 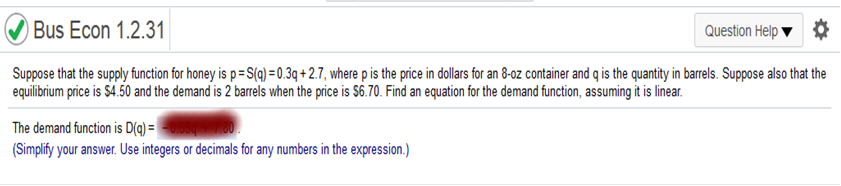
4.50 = .3q + 2.7 (subtract 2.7) 1.8 = .3q Q = 6 the demand is 2 barrels when the price is $6.70 and the demand is 6 barrels when the price is $4.50 6.70 – 4.50 / 2 – 6 -.55 P - 6.70 = -.55(q – 2) P – 6.70 = -.55q + 1.1 (add 6.70) P or D(q) = -0.55q + 7.80 Let one week's supply and demand functions for gasoline be given by p=D(q)=294−5/3q and p=S(q)=2/3, where p is the price in dollars and q is the number of 42-gallon barrels. (a) Graph these equations on the same axes. (b) Find the equilibrium quantity. (c) Find the equilibrium price. 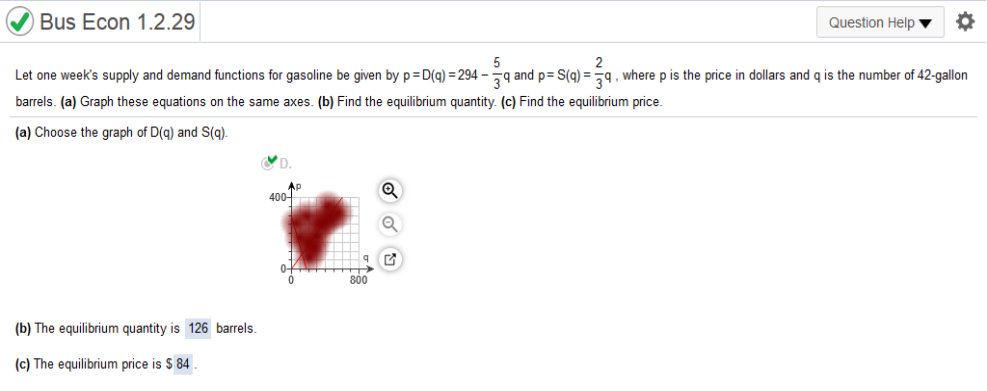
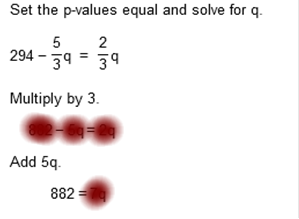 

294 – 5/3q = 2/3q (multiply by 3) 882 – 5q = 2q (add 5q) 882 = 7q (divide by 7) Q = 126 P = 2/3(126) = $84 Use the information listed below to solve parts a through h. Suppose that the demand and price for a certain model of a youth wristwatch are related by the following equation p = D(q) = 16 = 1.25q where p is the price (in dollars) and q is the quantity demanded (in hundreds). Find the price at each level of demand. Answer parts a through d. 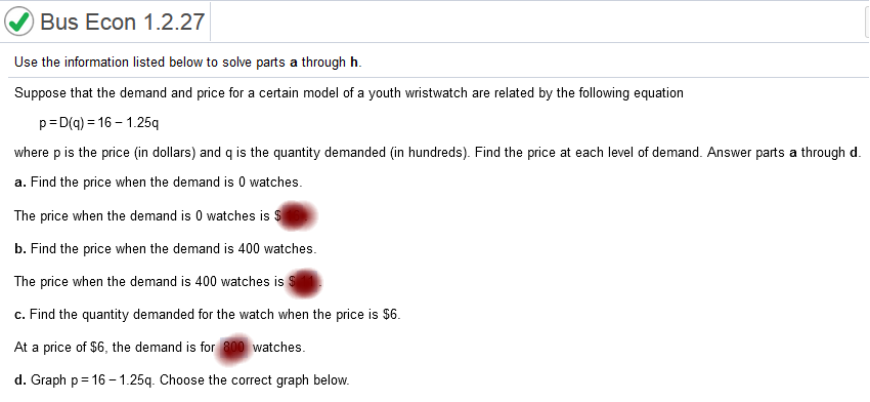 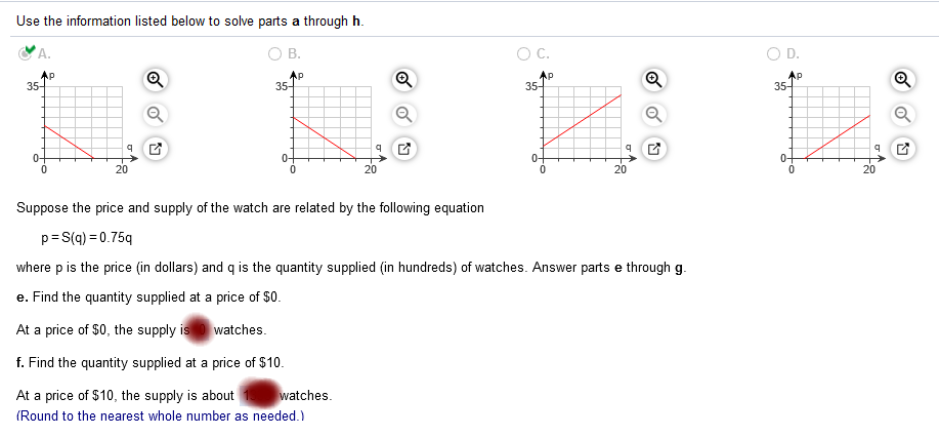 
p = D(q) = 16 = 1.25q Find the price when the demand is 0 watches. 16 – 1.25q(0) 16 – 1.25 The price when the demand is 0 watches is 16 16 – 1.25(4) 16 – 5 = 11 The price when the demand is 400 watches is $11 Find the quantity demanded for the watch when the price is $6. At a price of $6, the demand is for ___ watches. 6 = 16 – 1.25q (subtract 16) -10 = -1.25q (divide -1.25) Q = 8 x 100 = 800 At a price of $6, the demand is for 800 watches. Suppose the price and supply of the watch are related by the following equation p = S(q) = 0.75q where p is the price (in dollars) and q is the quantity supplied (in hundreds) of watches. Answer parts e through g. p = .75q 0 = .75q P = .75q (10) = .75 (divide by .75) 13.333 Multiply by 100 = 1333 16 – 1.25q = .75q (add 1.25) 16 = 2q (divide by 2) 8 multiply by 100 = 800 watches .75(8) = $6 Suppose that the demand and price for a certain model of a youth wristwatch are related by the following equation. p = D(q) = 16 = 1.25q where p is the price (in dollars) and q is the quantity demanded (in hundreds). Find the price at each level of demand. Answer parts a through d.   
p = D(q) = 16 = 1.25q a. Find the price when the demand is 0 watches. 16 – 1.25(0) 16 – 0 The price when the demand is 0 watches is 16. b. Find the price when the demand is 400 watches. 16 – 1.25(4) 16 – 5 = 11 The price when the demand is 400 watches is $11. c. Find the quantity demanded for the watch when the price is $6. Explanation At a price of $6, the demand is for ___ watches. 6 = 16 – 1.25q (subtract 16) -10 = -1.25q (divide -1.25) Q = 8 x 100 = 800 At a price of $6, the demand is for 800 watches. Suppose the price and supply of the watch are related by the following equation p = S(q) = 0.75q where p is the price (in dollars) and q is the quantity supplied (in hundreds) of watches. Answer parts e through g. p = .75q 0 = .75q Explanation P = .75q (10) = .75 (divide by .75) 10 / .75 = 1.3333333333 13.333 x 100 = 1333 16 – 1.25q = .75q 16 = 1.25q + .75q = 16 = 2q q = 16 / 2 = q = 8 8 x 100 = 800 .75(8) = $6 The table gives the revenue, R of a fast food chain, where R is in millions of dollars and t is in years since January 1, 2002. Complete parts a-d below 
a) Find the average rate of change in revenue over the one-year intervals from 2002 to 2003, from 2003 to 2004 and from 2004 to 2005 f(b) – f(a) / b – a 
b) Assuming the pattern repeats, find the average rate of change over the one-year intervals from 2005 to 2006 and from 2006 to 2007. 
c) Study the table of values. What can be inferred about the function R(t) from t = 0 to t = 5? 
d) Report and interpret the slope if the revenue is linear. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. 
Report and interpret the y-coordinate of the vertical intercept if the revenue is linear. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. 
Revenue R increases steadily at 5 points Choose the best answer for the limit. 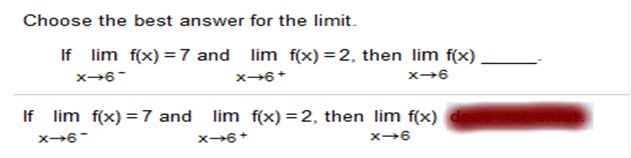
Does not exist. x-->6- x-->6+ What can you say about lim f(x)? x-->6 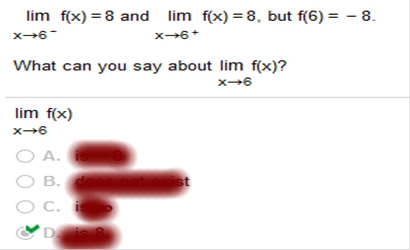
lim f(x)? is 8 x --> 6 Homework Chapter
1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM Need A Tutor? Need Homework Help?
|
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |