|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Homework Chapter
1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM Need A Tutor? Need Homework Help?
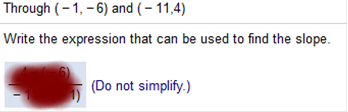
Calculus For Business Homework Chapter 1 Part A Write the expression that can be
used to find the slope.
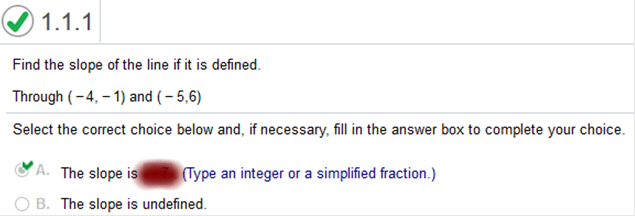
Answer: The slope is -1 Explanation: Online Calculator Find the slope of the line, if it is defined. Through (-4,-1) and (-5,6)
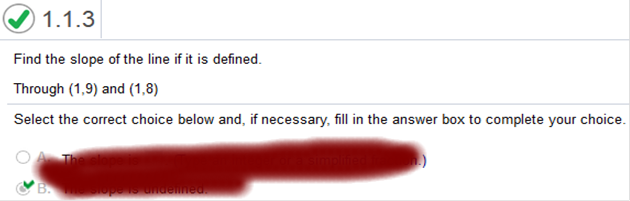
Join Now For Answers & Help!!! Online Calculator Find the slope of the line if it is defined. Through (1,9) and (1,8)
Join Now For Answers & Help!!! Online Calculator 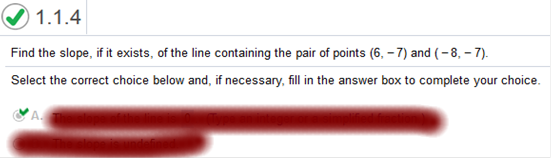
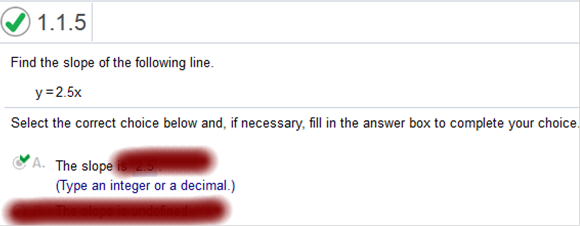
Explanation: Join Now For Answers & Help!!! Online Calculator Find
the slope of the following line
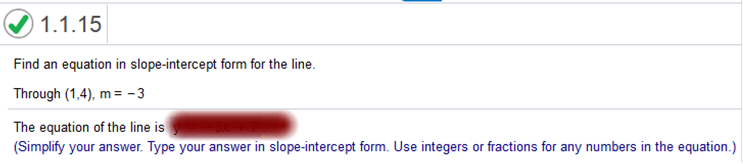
Find an equation in the
slope-intercept form for the line
Explanation Find
an equation in slope-intercept form for the line
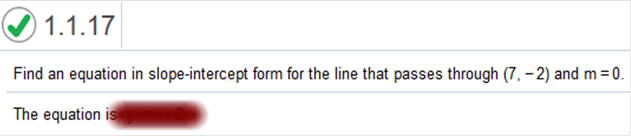
Explanation; Join Now For Answers & Help!!! Find an equation in slope-intercept form for the line that passes through (7,-2) m=0.
Explanation Join Now For Answers & Help!!! Find an equation of the line that contains the following pair of points (3,3) and (1,6)
Join Now For Answers & Help!!!
Slope Calculator Join Now For Answers & Help!!!
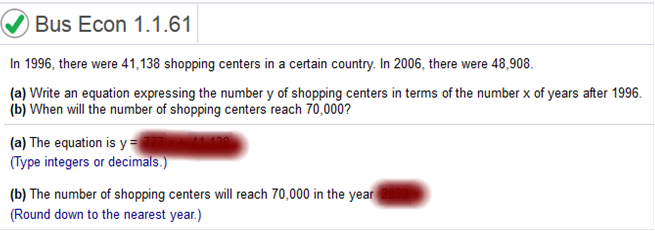
In 1996, there were 41,138 shopping centers in a certain country. In 2006, there were 48,908. a. Write an equation expressing the number y of shopping centers in terms of the number x of years after 1996. b. When will the number of shopping centers reach 70,000?
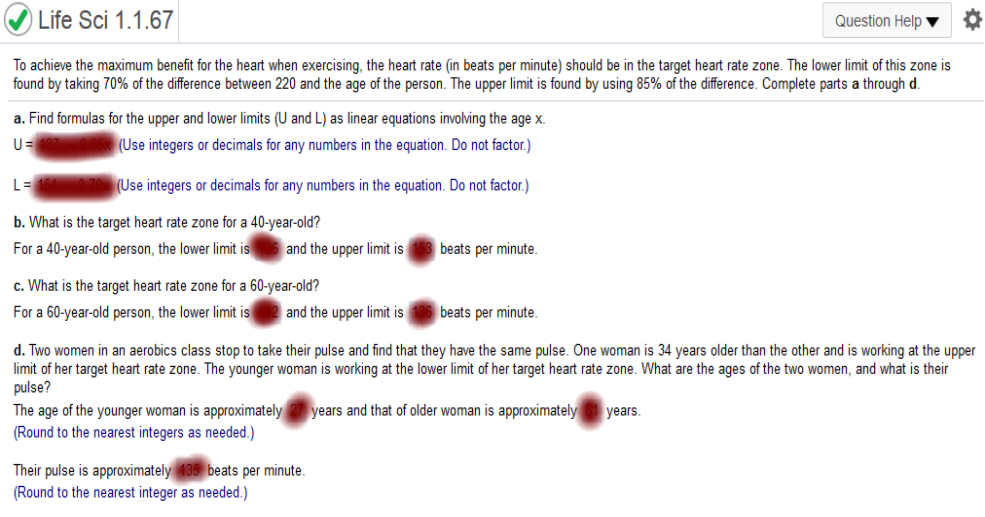
a. y2 – y1 / x2 – x1 48908 – 41138 / 10 – 0 = 777 y – 41138 = 777(x-0) = y = 777x + 41,138 b. 70000 = 777x + 41138 70,000 – 41,138 = 777x = 28,862 = 777x = 28,862 / 777 = x x = 37.145 1,996 + 37.145 = 2033 target heart rate zone. The lower limit of this zone is found by taking 70% of the difference between 220 and the age of the person. The upper limit is found by using 85% of the difference. Complete parts a through d.
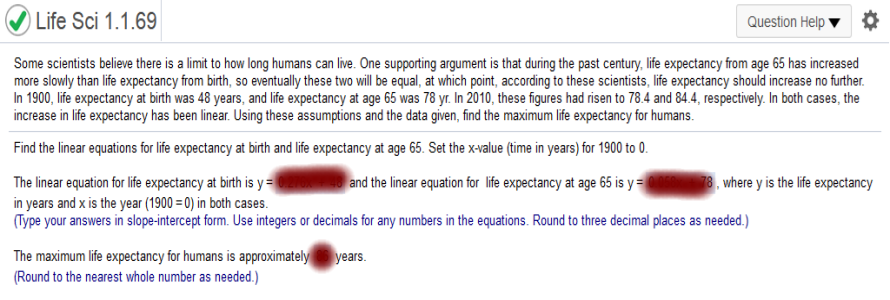
187 - 0.85x L = .7(220 – x) = L = 154 – 0.70x What is the target heart rate zone for a 40-year-old? For a 40-year-old person, the lower limit is ___ and the upper limit is ___ beats per minute. L = 154 – 0.70(40) = 126 U = 187 - 0.85(40) = 153 What is the target heart rate zone for a 60-year-old? For a 60-year-old person, the lower limit is ___ and the upper limit is ___ beats per minute L = 154 – 0.70(60) = 112 U = 187 - 0.85(60) = 136 Two women in an aerobics class stop to take their pulse and find that they have the same pulse. One woman is 34 years older than the other and is working at the upper limit of her target heart rate zone. The younger woman is working at the lower limit of her target heart rate zone. What are the ages of the two women, and what is their pulse? Younger = x + 34 154 - .7x = 187 - .85(x + 34) 154 - .7x = 187 - .85x – 28.9 154 - .7x = 158.1 - .85x Add .85x to both sides = 154 + .15x = 158.1 Subtract 154 from both sides = .15x = 4.1 = divide both sides by .15 = x = 27.333 (27) X + 34 = 61 27 and 61 Their pulse is approximately __ beats per minute. 154 - .7(27) = 135.1 (135) life expectancy from age 65 has increased more slowly than life expectancy from birth, so eventually these two will be equal, at which point, according to these scientists, life expectancy should increase no further. In 1900, life expectancy at birth was 48 years, and life expectancy at age 65 was 78yr. In 2010, these figures had risen to 78.4 and 84.4, respectively. In both cases, the increase in life expectancy has been linear. Using these assumptions and the data given, find the maximum life expectancy for humans. Find the linear equations for life expectancy at birth and life expectancy at age 65. Set the x-value (time in years) for 1900 to 0. The linear equation for life expectancy at birth is y = __ and the linear equation for life expectancy at age 65 is y = ___ , where y is the life expectancy in years and x is the year (1900 = 0) in both cases.
The data points are (0,48) (110,78.4) 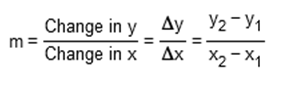
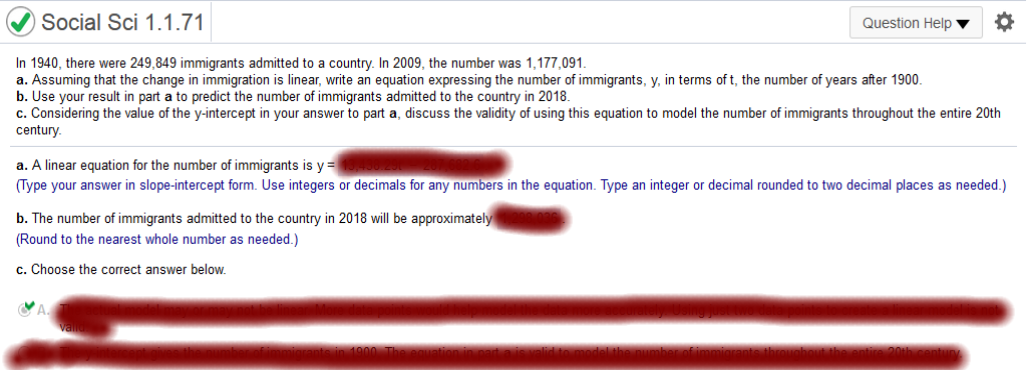
78.4 – 48 / 110 – 0 = .276 = The slope of the linear equation is 0.276. y = 0.276x + 48 life expectancy at age 65 (0,78) and (110,84.4) 84.4 – 78 / 100 – 0 = .058 = y = .058x + 78 0.276x + 48 = 0.058x + 78 = 0.276x = 0.058x + 30 = x = 138 y = 0.276(138) + 48 = 86 In 1940, there were 249,849 immigrants admitted to a country. In 2009, the number was 1,177, 091. a. Assuming that the change in immigration is linear, write an equation expressing the number of immigrants, y, in terms of t, the number of years after 1900. b. Use your result in part a to predict the number of immigrants admitted to the country in 2018. c. Considering the value of the y-intercept in your answer to part a, discuss the validity of using this equation to model the number of immigrants throughout the entire 20th century. A linear equation for the number of immigrants is y =
Let t1, y1 = (40,249849) and t2,y2 = (109,1177091) 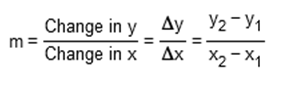
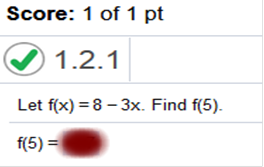
1177091 – 249849 / 109 – 40 = 13438.29 = 13438.29 y – 249849 = 13438.29(t – 40) = y – 249849 = 13438.29t – 537531.6 = y = 13438.29t – 537531.6 + 249849 = A linear equation for the number of immigrants is y = 13438.29t – 287682.6 Use your result in part a to predict the number of immigrants admitted to the country in 2018 t = 2018 – 1900 = 118 13438.29(t = 118) – 287682.6 = 1298035.62 The answer is: 1,298,036 The number of immigrants admitted to the country in 2018 will be approximately 1298036 Choose the correct answer below. A. The actual model may or may not be linear. More data points would help model the data more accurately. Using just two data points to create a linear model is not valid. B. The y-intercept gives the number of immigrants in 1900. The equation in part a is valid to model the number of immigrants throughout the entire 20th century Find f(5)
Explanation 8 – 3(5) = 8 – 15 = -7 f (5) = -7 The answer is: -7
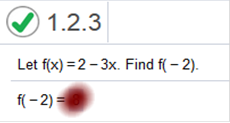
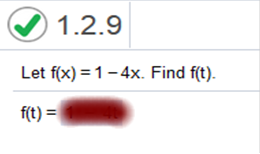
Let f(x) = 2 – 3x. Find f(-2)
Explanation 2 – 3(-2) = 8 Let f(x) = 1 – 4x. Find f(t)
Explanation Describe what fixed
costs and marginal costs mean to a company. A. Fixed cost is the
constant for a particular product and does not change as more items are made. Marginal cost is constant for a particular product and does not change as more items are made. Explain why a linear function may not be adequate for describing the supply and demand functions. A. If
the rate of change of the price is a constant, a linear function may not be
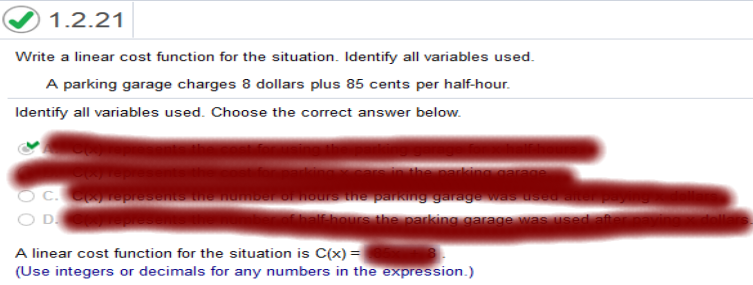
adequate for describing the supply and demand functions. Write a linear cost
function for the following situation.
Explanation Write a linear cost
function for the situation. Identify all variables used.
A. C(x) represents the
cost for using the parking garage for x half-hours. Homework Chapter
1A 1B 2A 2B 3A 3B 4A 4B 5A 6A Chapter Tests 1 2 3 4 5 6 7 FINAL EXAM Need A Tutor? Need Homework Help?
|
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |