Calculus For Business
Final Exam
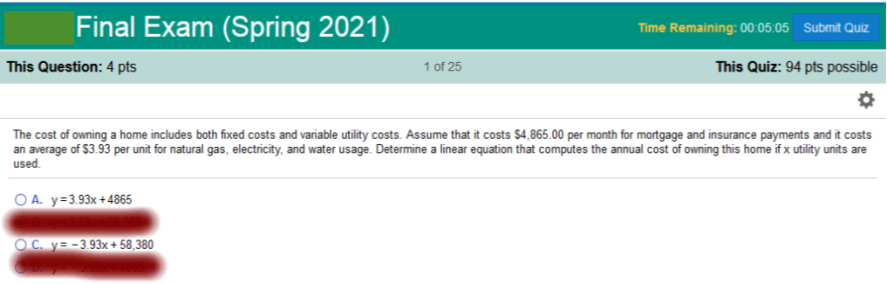
The cost of owning a
home includes both fixed costs and variable utility costs. Assume that it costs
$4,865.00 per month
for mortgage and insurance payments, and it costs an
average of $3.93 per unit for natural gas, electricity, and water usage.
Determine a linear equation that computes the annual cost of owning this home
if x utility units are used.
Steps:
Join Now For Answers & Help!!!
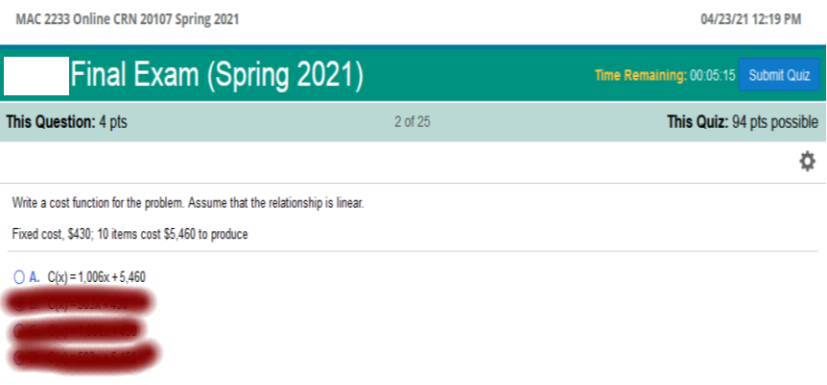
Write a cost function
for the problem. Assume that the relationship is linear.
Fixed cost, $43; 10
items cost $5,460 to produce.
Solve:
Join Now For Answers & Help!!!
A toilet manufacturer
has decided to come out with a new and improved toilet.
The fixed cost for the production of this new toilet line is $16,600 and
the variable costs are $67 per toilet.
The company expects to
sell the toilets for $156.
Formulate a function
P(x) for the total profit from the production and sale of x toilets.
Join Now For Answers & Help!!!
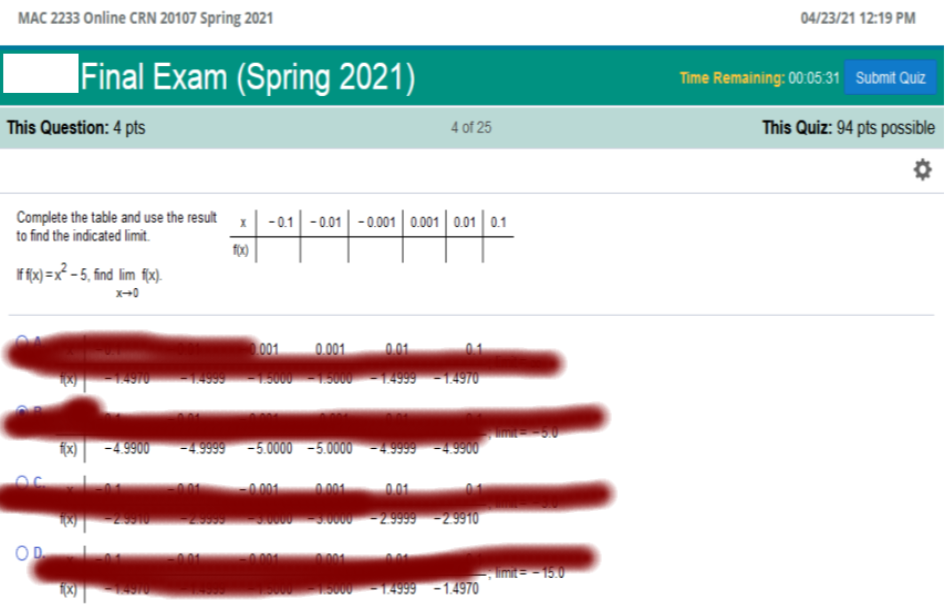
Complete the table and
use the result to find the indicated limit
If f(x) = x2
– 5, find lim (fx)
x-->0
Steps
Join Now For Answers & Help!!!
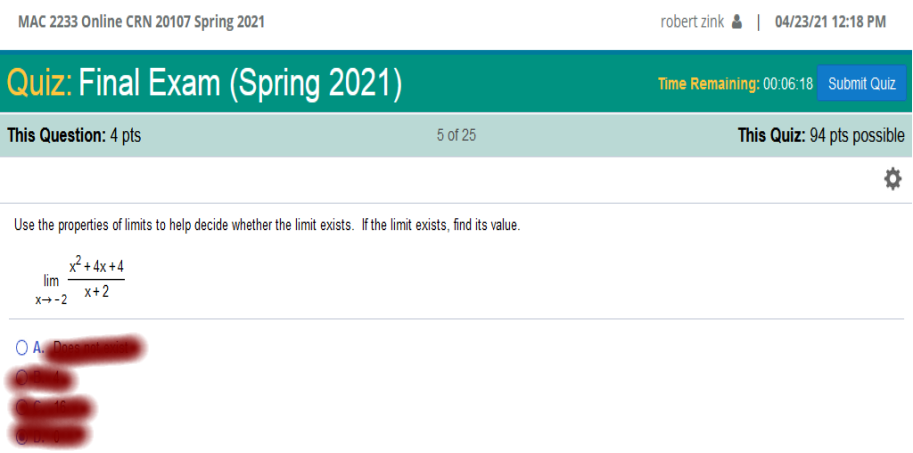
Use the properties of the limits to help decide
whether the limit exists. If it exists, find the value.
Steps
Join Now For Answers & Help!!!
Use the properties of
the limits to help decide whether the limit exists. If it exists, find the
value.
Steps
Join Now For Answers & Help!!!
The total cost to
produce x handcrafted wagons is C(x) = 110 + 8x – x2 + 7x3.
Find the marginal cost when x = 5.
Explanation:
Join Now For Answers & Help!!!
Use the quotient rule to find the derivative.
f(x) = 
Steps
Join Now For Answers & Help!!!
The total profit from selling x units
of cookbooks is P(x) = (4x - 9) (8x - 6).
Find the marginal average profit
function, 
'(x).
Steps
Join Now For Answers & Help!!!
Find the derivative
√4x + 2
Find the derivative.
√4x + 2
(4x + 2)1/2 – 1 x 4x + 2
Reduce
= 
The sales in thousands
of a new type of product are given by S(t) = 240 - 40e-0.5t,
where t represents time
in years. Find the rate of change of sales at the time when t = 2.
(Round to
the nearest tenth).
The value
of e is 2.718281828459045
Find the derivative
and plug in the value for t which = 2
240 - 40e-0.5t
240 x 0 =
0
-40 e
(-.5) .5 – 1 = 20e-.5
20(2.718281828459045)
-.5(2)
20(2.718281828459045)-1
= 7.357588823
Round to
the nearest tenth = 7.4
The ph scale
is used by chemists to measure the acidity of a solution it is a base 10
logarithmic scale.
The pH, P, of a solution and its
hydronium ion concentration in moles per liter, H, are related as H = 10-P.
Find the formula for the rate of
change 
Solution
ln h = ln (10-p)
ln h = (-p) ln (10)
(-p ln (10))
-ln(10) 
= H[-ln (10)]
= -10-p ln (10)
Find the derivative of the function.
y = log(4x)
y1 = log(4x)
= 
Simplify
Assume that the total revenue received from the sale of x items is
given by R(x) = 37 ln(3x+1),
while the total cost to produce x items is
C(x)=x/3.
Find the approximate number of items that should be manufactured so
that the profit,
R(x) - C(x) is a maximum.
P(x) = R(x) – C(x)
Write the equation 37
ln (3x + 1) - 
Now we find the derivative, set P(x) to zero, and solve for x.
Find
the derivative of 37 ln (3x + 1) - 
set P(x) to zero, and solve for x
- 
= o
111 = 
(3 x 111 = 333) and (3
/ 3 = 0)
333 = 3x + 1 Subtract 1 from both sides = 332 = 3x
Divide both sides by 3 = x = 332 / 3
x = 110.66666667
Round to 111
The annual revenue and
cost functions for a manufacturer of grandfather clocks are approximately
R(x) = 520x – 0.03x2
and C(x) = 160x + 100,000
where x denotes the
number of clocks made. What is the annual maximum profit?
Same
formula as above
P(x) =
R(x) – C(x)
520x –
0.03x2 - 160x - 100,000 (note that we subtract both numbers with
C(x)).
Now we
simplify and put it in proper order.
-.03x2
+ (520x – 160x) - 100,000 = -.03x2
+ 360x - 100,000
Now we
find the derivative and set P(x) to equal zero. = -0.06x +
360 = 0
360 =
0.06x
x = 360 /
0.06 = x = 6,000
Now we
plug 6,000 in the original formula P(x) = R(x) – C(x) which is
520x –
0.03x2 - 160x - 100,000
520(6,000)
– 0.03(6,000)2 – 160(6,000) - 100,000
3,120,000 -
1,080,000 - 960,000 - 100,000
3,120,000
- 1,080,000 = 2,040,000 – 960,000 = 1,080,000 – 100,000 =
980,000
Find the number of
units(x) that produces the maximum profit(P), if C(x) = 85 + 24x and p = 40 -
2x
P(x) =
R(x) – C(x)
First, we
need to factor P(x)
40 – 2x(x)
= 40x – 2x2
40x – 2x2
– 85 – 24x (note we subtract both numbers in C(x))
Simplify
and put back in proper order.
-2x2
+ (40x – 24x) – 85 = -2x2
+ 16x – 85
Now we
find the derivative of -2x2 + 15x – 85 = 4x + 16
Now we
set to equal zero and solve for x. = 4x + 16 =
0
16 = 4x divide both sides by 4 = x = 16 /
4
x = 4
Now we
plug 4 into the derivative 4x + 16.
4(4) + 16
= 32
A rectangular field is
to be enclosed on four sides with a fence.
Fencing costs $5 per foot for two
opposite sides, and $6 per foot for the other two sides.
Find the dimensions of
the field of area 620 ft2 that would be the cheapest to enclose.
Formula required: 5(2x) + 6 (
)
Now we simplify 10x + 6 (
) = 10x + (
)
Next we set equal to 0 = 10 - (
) = 0 and simplify - = -10
We simlify further: -10x2 =
-7440
Next we divide both sides by -10 = x2 = 744
Next we need to square 744 to solve for x: x = √744
x = 27.2763639 (round to 2 decimal places) x = 27.3
Since the dimensions of the field is equal to 620, we need to divide that by 22.3
620 / 22.3
620 / 27.3 =
22.73560689
x = 22.3, y = 27.3
Given the demand
function q = 401 - 4p calculate the elasticity of the demand when p = 53.
The
formula for this problem is:
Now
plug in the value of P (53)
212
/ 189 = 1.121693122
The
elasticity of the demand = 1.12
Given the revenue and
cost functions R(x) = 28x - 0.6x2 and C(x) = 6x + 9, where x is the
daily production, find the rate of change of profit with respect to time when
10 units are produced and the rate of change of productions is 7 units per day
28x –
0.6x2 – 6x – 9
First, we
simplify to 22x -
0.6x2 – 9
Derivative
-1.2x +
22
-1.2 x 10
+ 22 x 7
154 – 12
= 142
Evaluate the definite
integral.
∫ (5x2
− 8x + 6) dx
Apply
linearity: = 5 ∫ x2
dx – 8 ∫ x dx + 6 ∫ 1 dx
Now
solving: ∫ x2
dx Apply
power rule: ∫ xn dx = 
= 
Now
solving: ∫ x dx Apply
power rule with n = 1 =
Now
solving: ∫ 1 dx Apply
constant rule: = x
Plug in
solved integrals: 5 ∫ x2
dx – 8 ∫ x dx + 6∫ 1 dx = 
– 4x2
+ 6x
Evaluate the definite
integral.
37791 /
24010000 = 0.0015739692 = round
to 0.0016
Find the integral.
x2 (3x + x-3)
dx
Find the integral:
-7t^2 dt
∫e
Simplify 
du
Since −1 is constant
with respect to u, move −1 out of the integral.
-∫ 
du
Since 
is constant with respect to u,
move out of the integral.
∫ eu du)
The integral of eu with respect to u is eu.
− (eu + C)
Simplify. − eu + C
Replace all
occurrences of u with −7t2 − e-7t2 + C
The number of books in
a library increases at a rate according to the function B’(t) = 171e0.03t,
where t is measured in years after the library opens.
How many more books will the library have 2 year(s) after opening?
|
We need to evaluate
the integral
 e0.03t
171 is constant with
respect to t,
we move 171 out of the
integral.
 e0.03t
u = 0.03t, then du =
0.03t or  du = dt
Now we rewrite the
equation.
Combine 
Next, we move  out of the integral
|
Factor and combine. 
(the integral of eu is eu
so we move that out)
e = 2.71828, and u = .006
so now we set up the equation to
factor
 (2.718280.06) -
171 / 0.03 = 5,700
5,700 x 2.718280.06 - 
6,052.468071
– 5,700 = 352.468071
Round
to 352
|
The price per share of
a stock can be approximated by the function S(t) = t(30
– 30t) + 25,
where t is time (in years) since the
stock was purchased.
Find the average price of the stock over the first 8
years.
(Round the answer to two decimal places if necessary).
This is the
integral we need to solve!
You can
solve this one yourself!
This
calculator will solve it for you.
https://www.integral-calculator.com
It will
not solve some of the integral problems, so it is best to learn!