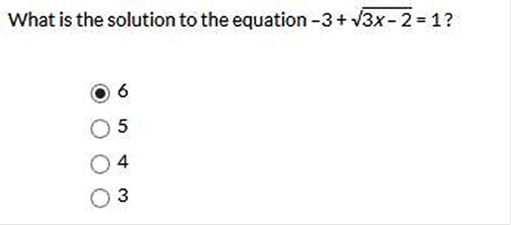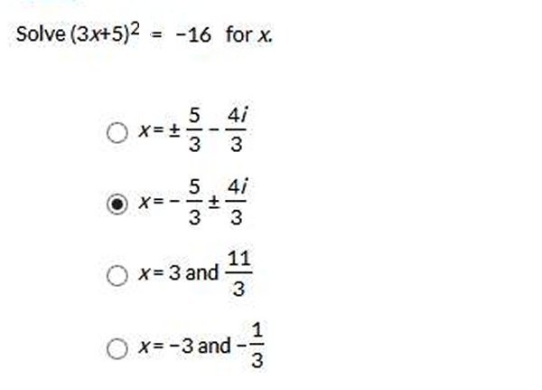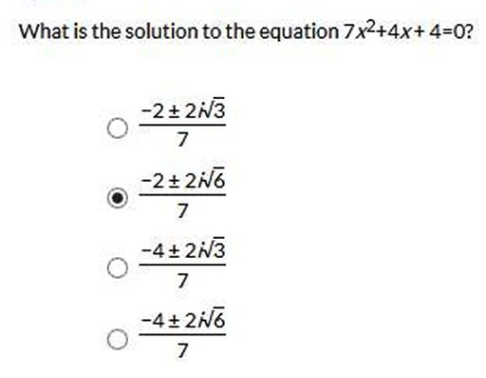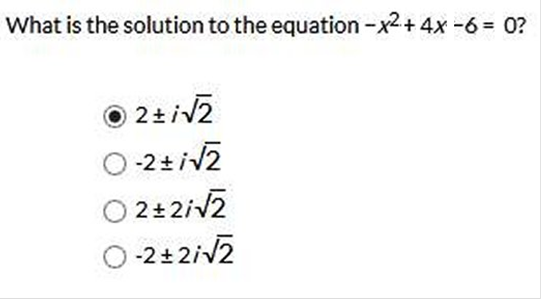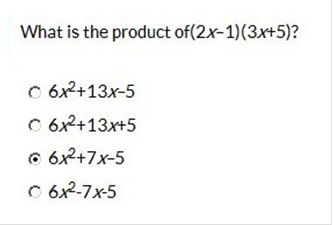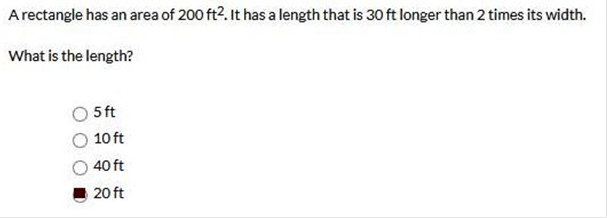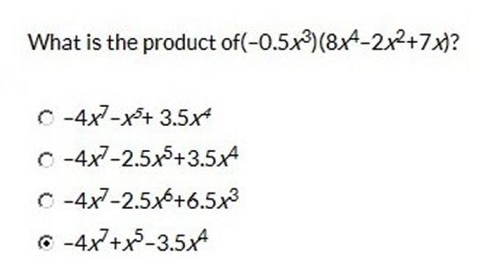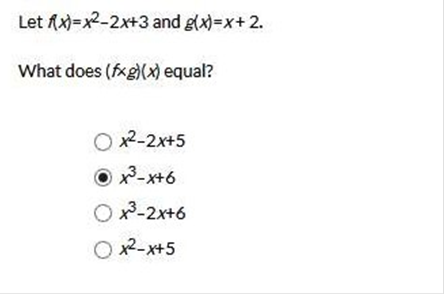College Algebra
(MAC-1105C) - Final Exam (Proctored)
College Algebra (4
Credit Hours)
- These problems are from Proctor U - Proctored Exam.
The proctored exam
had 50 questions, however there are 69 questions on these pages.
I have the
steps to solve the problems which should help you with any College Algebra Final Exam.
Page 2
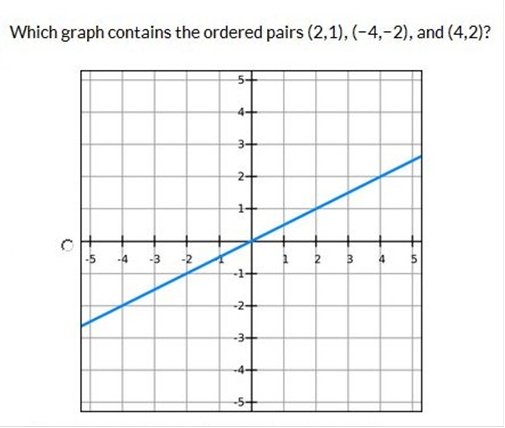
To plot (2, 1), start at the origin (0,0) and move
right 2 units and up 1 unit = (2,1)
To plot (−4, −2), start at the origin (0,0) and move
left 4 units and down 2 units = (−4,−2)
To plot (4, 2), start at the origin (0,0) and move
right 4 units and up 2 units. = (4,2)
y = -4x + 12
We are given the value of y = (-4)
(-4) = -4x + 12
-4 = -4x + 12
-4 – 12 = -4x -12 – 12
-16 = -4x
= 
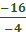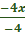= 4 = x
5 =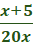 
5 = x + 
5 = 1.25x
5 ÷ 1.25 = 4
x = 4
College Algebra (MAC-2233) Lessons:
Pre-Assessment Exam
Final Exam (Proctored) Page
1 2 3
More Lessons 1 2
3 4 5 6 7 8 9 10 11 12 13 14
15 16 17 18 19 20 21 22
23 24 25
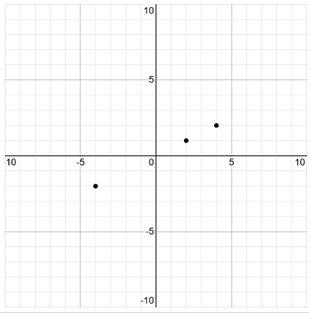
With this problem we need to plug in the values of the ordered pairs and see which equations match.
I have done this below!
First equation: 3 = -2(-4) – 5 | 3 = 8 - 5 | 3 = 3 Matches the ordered pairs!
Second equztion: 3 = -(-4) -1 | 3 = 4 – 1 | 3 = 3 Matches the ordered pairs!
Third eqution: 3 = -4 – 7 | 3 = -11
Does not match!
Fourth equation: 3 = 2(-4) + 8 | 3 = -8 + 8 | 3 =
0 Does not match!
We have already worked on a similar
problem. We cross-multiplied!
So, we multiply the numerator (top) of the first fraction by the denominator
(bottom)
of the second fraction. And vice versa
2(x − 4) = x ⋅ 5 = 2x – 8 = x ⋅ 5
Move 5 to the left
of x 2x – 8 = 5x
Move all terms
containing x to the left side of the equation.
−3x – 8 = 0
Add 8 to both sides
of the equation. −3x = 8
Divide each term in
−3x = 8 by −3 and simplify.
x = The result can
be shown in multiple forms. Exact Form:
x=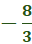
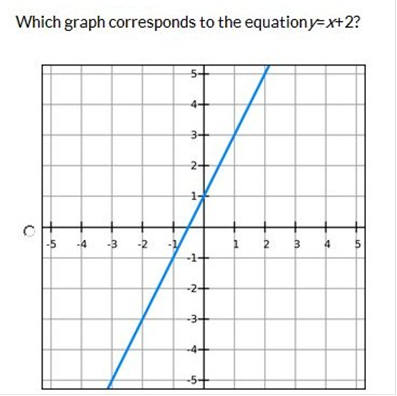
y = x + 2
The slope-intercept form
is:
y = mx + b where
m = the slope
b = y-intercept
We find the values of m
and b using the form y = mx + b
We know m = 1, because m
is next to x. 1x is the same as x.
So, we know m = 1 and b =
2.
And we know the value of y
= 1 + 2.
We now have two ordered
pairs.
x = 0, y = 2 or (0, 2)
x = 1, y = 3 or (1, 3)
Now we can plot the
equation y = x + 2
1x5 x 1x-3
1 x 1 = 1
x5 x 1x-3 = 5
+ -3 = x2
College Algebra (MAC-2233) Lessons:
Pre-Assessment Exam
Final Exam (Proctored) Page
1 2 3
More Lessons 1 2
3 4 5 6 7 8 9 10 11 12 13 14
15 16 17 18 19 20 21 22
23 24 25
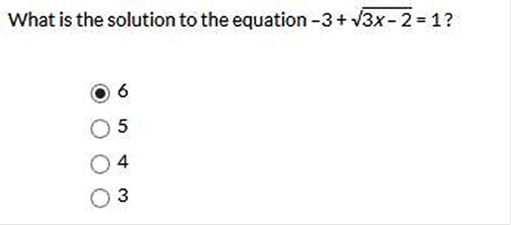
This looks more difficult than it really is!
First, we need to remove the radical -3 from the left side.
We do this by adding it to the right side of the = sign and
adding it to 1
however, we need to square the result. So, we are left
with:
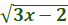= 12 + 32 = 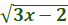= 42
Now this is much more manageable.
Now we simplify both sides of the equation.
42 = 16
Since there is a variable inside a radical, the square root
is ½ power.
Really, we can remove the radical all together,
however, we will be formal since this might be the first
time for some students.
To simplify the radical, we do the following:
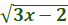= ((3x – 2)1/2)2 you see ½ and 2
cancel out the radical.
So, we are left with:
3x – 2 = 16
Now we add 2 to both sides and divide both sides by 3.
3x
– 2 + 2 = 3x, and 16 + 2 =
18
we left with 3x = 18
18 / 3 = 6
x = 6
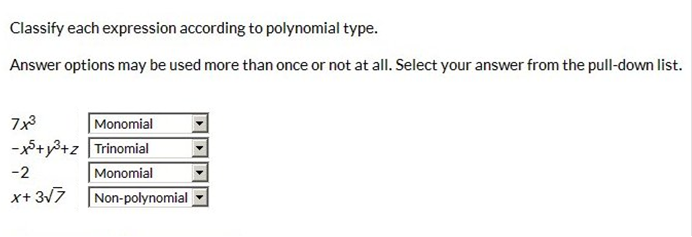
1st has only one term.
2nd has 3 terms.
3rd has 1 term.
4th is not a polynomial because it has a square root.
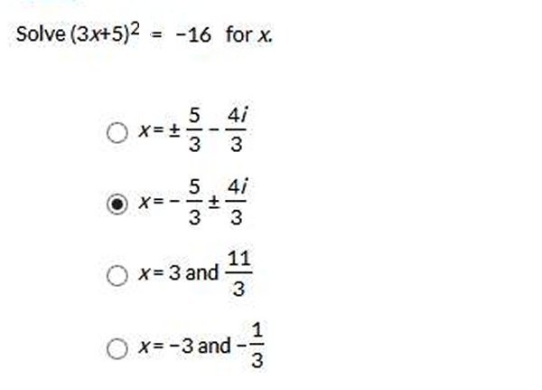
Take the specified
root of both sides of the equation to eliminate the exponent on the left side.
3x +5 = ±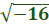 
Simplify 3x +5 = ±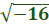
3x + 5 = ± 4i
The complete
solution is the result of both the positive and negative portions of the
solution.
First, use the
positive value of the ± to find the first
solution.
3x + 5 = 4i
Move all terms not
containing x to the right side of the equation.
3x = −5 + 4i
Divide each term in
3x = −5 + 4i by 3 and simplify.
x = -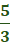
± 
College Algebra (MAC-2233) Lessons:
Pre-Assessment Exam
Final Exam (Proctored) Page
1 2 3
More Lessons 1 2
3 4 5 6 7 8 9 10 11 12 13 14
15 16 17 18 19 20 21 22
23 24 25
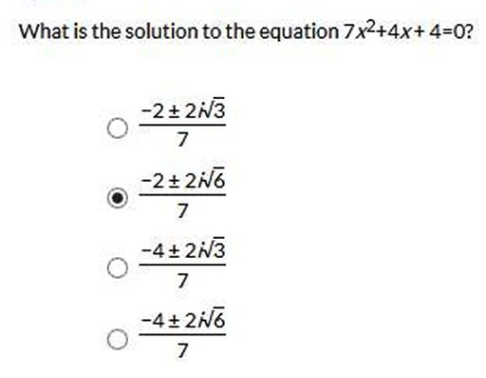
a b c
7x2 + 4x + 4 = 0
Use the quadratic
formula to find the solutions.
= 
Simplify - Simplify the numerator.
Raise 4 to the power of 2 x =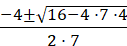 
Multiply −4 ⋅ 7 ⋅ 4
= 
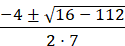
Subtract 112 from 16 = 
Rewrite −96 as −1(96)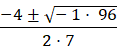 
Rewrite √−1(96)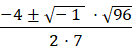 
Rewrite √−1 as i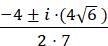 
Move 4 to the left of I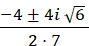 
Simplify 
simplify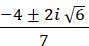 
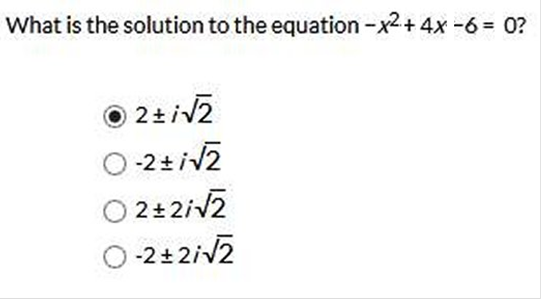
a b c
-x2 + 4x – 6
= 0
Use the quadratic formula to find the solutions.
= 
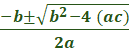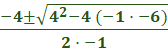
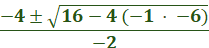
Follow the same steps as above!
x(x – 6y) = x2- 6xy +
12y(x-6y) =
12xy – 72y2
x2
– 6xy – 72y2
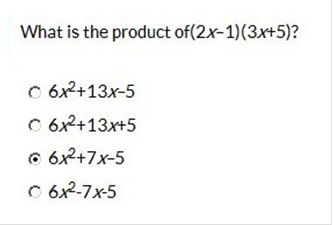
2x(3x + 5) = 6x2
+ 10x
-1(3x + 5) = -3x
– 5
6x2 + 7x - 5
College Algebra (MAC-2233) Lessons:
Pre-Assessment Exam
Final Exam (Proctored) Page
1 2 3
More Lessons 1 2
3 4 5 6 7 8 9 10 11 12 13 14
15 16 17 18 19 20 21 22
23 24 25
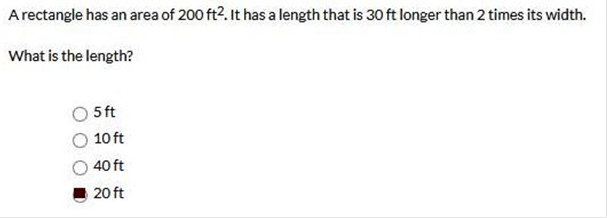
(2w + 30)w = 200 = 2w2 + 30w = 200 = 2w2 + 30w – 200 = 0
Solve for W 2(w – 5)(w
+ 20) = 0
w – 5 = 0
w = 0 + 5 = w = 5
w + 20 = 0
w = 0 – 20 = -20
Since the length is 30
ft longer than 2 times the width then
the length = 20 and
the width = 5
Let’s check the
answer.
The length is 30 ft
longer than 2 times the width and the area is the width
times the length
2 x 5 = 10
10 + 30 = 40
40 x 5 = 200
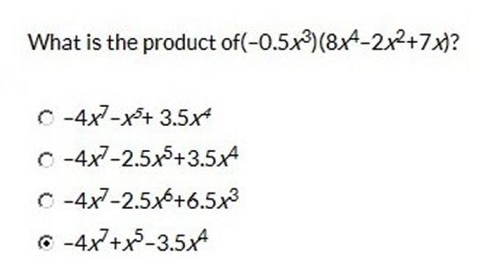
-0.5x3(8x4)
= -4x7
-0.5x3(-2x2)
= x5
-0.5x3(7x) = -3.5x4
-4x7 + x5 -3.5x4
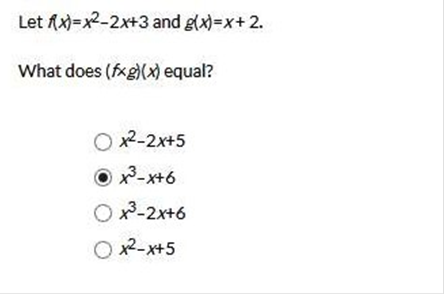
(x2 – 2x +
3)(x + 2)
x2(x + 2) = x3 + 2x2
-2x(x
+ 2) = -2x2 – 4x
3(x + 2) = 3x + 6
x3 – x + 6
Write for y
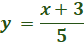
swap the variables.
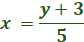
Solve for y
Multiple both sides by 5
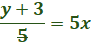
y + 3 = 5x (subtract by 3)
y = 5x = 3
Use the TI84 Plus or similar
calculator for this and enter as shown below.
25,000(20.025(4)) or
25,000(2.1) = 26,794.33656
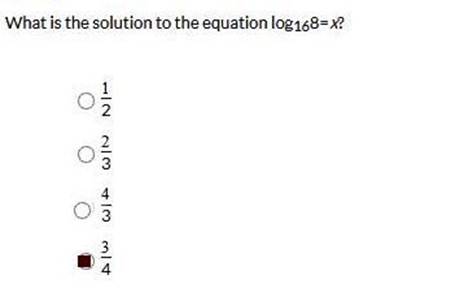
*Whenever there is no
base, the base is assumed as 10.
In this case, the base
is 16, so we write the equation like so and solve for x
by = x
16x = 8
Find equal bases.
(24)x
= 23
24x = 23
Divide both sides by 2.
4x = 3
Divide both sides by 4.
4/4 = 3/4, so x = ¾
A = Pert
A = the total amount = 10,000 + 20,000 = 30,000
30,000 = 20,000e0.055t
Divide both sides by 20,000.
1.5 = e0.055t
ln1.5 = 0.055t
t =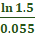 
Use TI84 Plus to solve. ln(1.5/0.055)
t =
7.372092875 = round to 7.4
8(3x2) = 24x2
8(5) = 40
Now we join the equation = 24x2 + 40
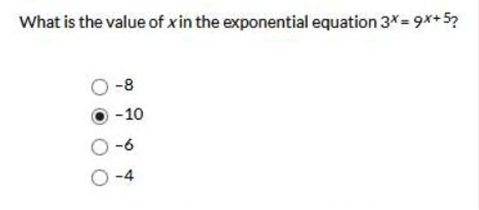
First create equal
bases by squaring 9.
3x = 32(x
+5)
Then divide both sides
by 3.
x = 2(x + 5) Then simplify x = 2x + 10
then subtract 2x from
both sides.
x – 2x = 10 simplify -x = 10
Then divide both sides
by -1 x = -10