|
Accounting | Business | Computer Science | General Studies | Math | Sciences | Civics Exam | Help/Support | Join/Cancel | Contact Us | Login/Log Out Need A Tutor? | Need Homework Help? Help and Support | Join or Cancel College Algebra
(MAC-1105C) - Final Exam (Proctored)
College Algebra (4
Credit Hours)
I have the steps to solve the problems which should help you with any College Algebra Final Exam. 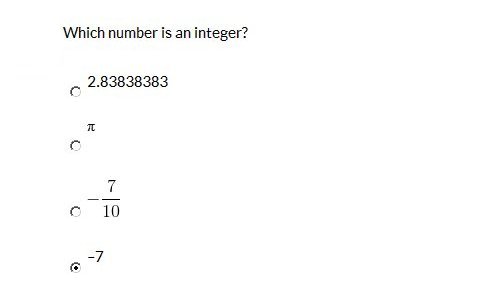
Explanation: Integers include positive numbers, negative numbers, and zero. 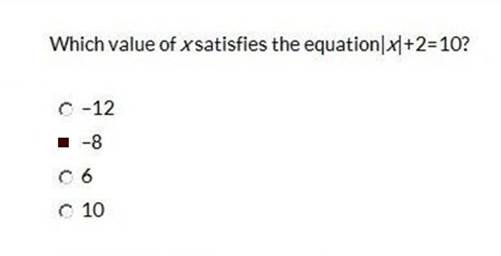 Explanation Move all terms not containing |x| to the right side of the equation. Ixl = 8 Remove the absolute value term. This creates a ± on the right side of the equation because Ixl = ± x x = ±8 First, use the positive value of the ± to find the first solution. x = 8 Next. use the negative value of the ± to find the second solution. x = -8 x = 8, -8 
Explanation -2 is less than +3 28 ÷ 7 = 4 = 4 is greater than 3 5 is greater than 3. 9/3 = 3 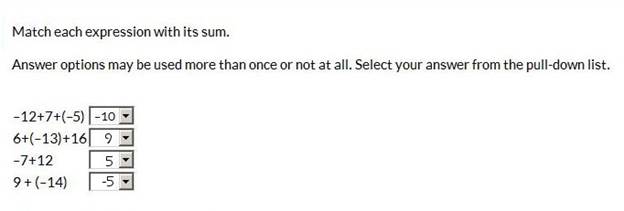
Explanation -12 + 7 = -5, -5 + -5 = -10 6 + (-13) = -7, -7 + 16 = 9 -7 + 12 = 5 9 + -14 = -5 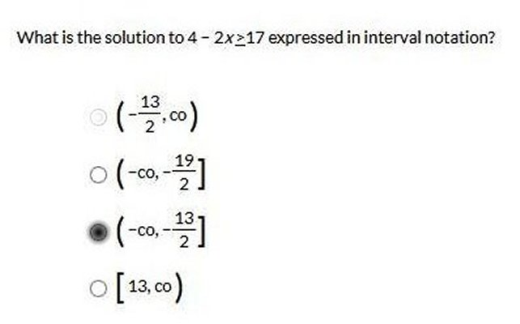 Explanation: Simplify both sides of the inequality: -2x + 4 ≥ 17 Subtract 4 from both sides -2x ≥ 13 Divide both sides by -2 X =  Explanation -19 – (-7) = -19 – (-7) = -19 + 7 Note that -1(-7) = 7 So, -17 + 7 = -12 the answer = -12 
Explanation: Product means to multiply. 5 · 4 = 20 College Algebra (MAC-2233) Lessons:
Pre-Assessment Exam
Final Exam (Proctored) Page
1 2 3
More Lessons 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 
Factor like terms and then combine. 7b – 3b = 4b 4b + 4 = 4b + 4 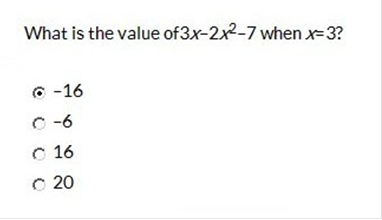
Substitute for x in the expression. 3(3) – 2(3)2 – 7 9 – 2(9) – 7 9 – 18 – 7 9 – 18 = -9 + -7 = -16 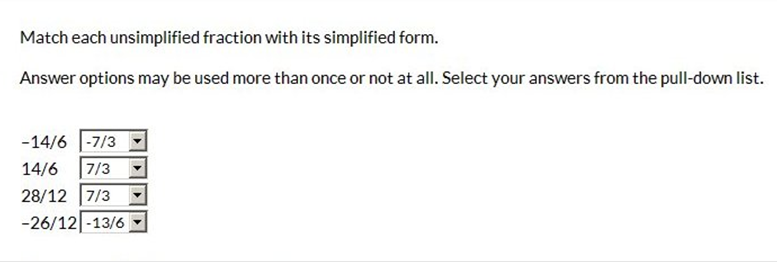
Divide both sides by like terms. -14/ 6 (both sides can be divided by 2) = -14 ÷ 2 = -7 and 6 ÷ 3 = 2 = -7/3 14/6 (both sides can be divided by 2) = 14 ÷ 2 = 7 and 6 ÷ 3 = 2 = 7/3 28/12 (both sides can be divided by 4) = 28 ÷ 4 = 7, and 12 divided by 4 = 3 = 7/3 -26/12 (both sides can be divided by 2) -26 ÷ 2 = -13, and 6 ÷ 2 = 3 = -13/6 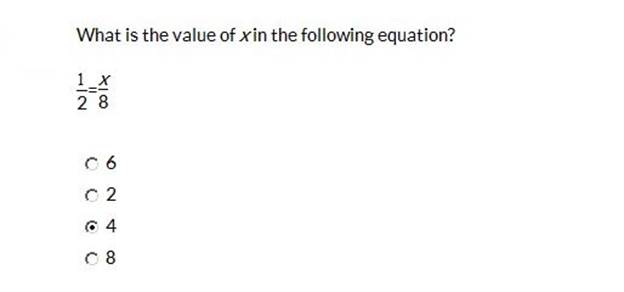 Explanation: The simplest way to do this is flip or cross multiply. Let’s cross multiply! Start from top left and multiply: 1 · 8 = 8 (8 goes on the top of the fraction) Now multiply: 2 · x = 2x (2x goes on the bottom of the fraction) Now we simply divide because we have : 8 / 2 = 4 x = 4 
Explanation Formulas: x + y = 72 .40x + .64y = 72(.55) y = 72 – x .40x + .64(72 – x) = 39.6 .40x + 46.08 - .64x = 39.6 -24x + 46.08 = 39.6 -.24x = -6.48 x = -.648 ÷ -.24 = 27 Blend A = x = 27 x + y = 72 27 + y = 72 72 – 27 = y 45 = y Blend B = y = 45 College Algebra (MAC-2233) Lessons:
Pre-Assessment Exam
Final Exam (Proctored) Page
1 2 3
More Lessons 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 
Explanation x + y = 5 .17x + .42y = 5(.32) y = 5 – x .17x + .42(5 – x) = 5(.32) .17x + 2.1 - .42x = 1.6 -.25x + 2.1 = 1.6 -.25x = -0.5 x = 2 17% blue paint x = 2 Check x + y = 5 2 + y = 5 y = 3 42% blue paint = y = 3 
Explanation x + y = 6 .30x + .07x = 6(.21) y = 6 – x .30x + .07(6 – x) = 6(.21) .30x + .42 - .07x = 1.26 .23x +.42 = 1.26 .23x = .84 x = 3.65 30% copper alloy = x = 3.65 Check x + y = 6 3.65 + y = 6 y = 2.35 7% copper = y = 2.35 
3 · 22 = 12 3 · -6 = -18 + 2 · 32 = 18 12 – 18 + 18 = 12 
Explanation x + y = 186 12x + 16y = 2640 y = 186 – x 12x + 16(186 – x) = 2640 12x + 2976 – 16x = 2640 -4x + 2976 = 2640 -4x = -336 x = 84 $12 tickets = x = 84 Check x + y = 186 84 + y = 186 y = 102 $16 tickets = y = 102 $12 (84) + $16 (102) = 2,640 1,008 +1,632 = 2,640 
Explanation x + y = 3,200 40x + 60x = 152,000 y = 3200 – x 40x + 60(3200 – x) = 152,000 40x + 192,000 – 60x = 152,000 -20x = 152,000 – 192,000 20x = -40,000 x = 2,000 $40 tickets = x = 2,000 x + y = 3,200 2,000 + y = 3,200 y = 1,200 Check 40(2,000) + 60(1,200) = 152,000 
Explanation 4 · 2 = 8 When multiplying exponents, the exponents are added. 4a5 · 2a8 = 813 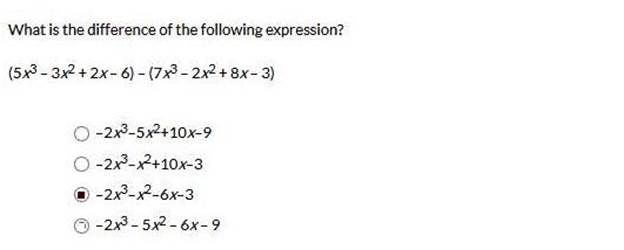 Simplify each term. Apply the distributive property. 5x3−3x2+2x−6−(7x3) − (−2x2) − (8x)− −3 Simplify. 5x3−3x2+2x−6−7x3+2x2−8x+3 Simplify by adding terms. Subtract 7x3 from 5x3 −2x3 − 3x2 + 2x – 6 + 2x2 − 8x + 3 Add −3x2 and 2x2 −2x3−x2+2x−6−8x+3 Subtract 8x from 2x −2x3−x2−6x−6+3 Add −6 and 3 −2x3−x2−6x−3 College Algebra (MAC-2233) Lessons:
Pre-Assessment Exam
Final Exam (Proctored) Page
1 2 3
More Lessons 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 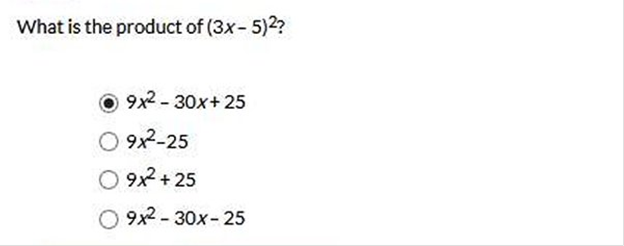 Explanation (3x – 5)2 = (3x – 5) (3x – 5) 3x · 3x = 9x2 -5 · 3x = -15x -5 · 3x = -15x -5 · -5 = 25 Now we combine like terms and simplify 9x2 (- 15x – 15x) + 25 9x2 – 30x + 25 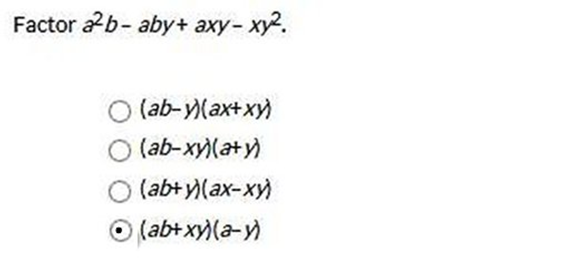 Explanation Factor out the greatest common factor from each group. Group the first two terms and the last two terms. (a2b − aby) + axy − xy2 Factor out the greatest common factor (GCF) from each group. ab (a − 1y) + xy (a − 1y) Factor the polynomial by factoring out the greatest common factor, a − 1y (a−1y) (ab + xy) Rewrite −1y as −y. (a − y) (ab + xy) 
Explanation x + .30x = 32.76 1.30x = 32.76 x = 32.76 ÷ 1.30 x = 25.20 Check 25.20 + 25.20(.30) = 32.76  Explanation For a polynomial of the form ax2 + bx + c, rewrite the middle term as a sum of two terms whose product is a ⋅ c = 2 ⋅ 5 = 10 and whose sum is b = −7. Factor −7 out of −7x 2x2−7(x) + 5 Rewrite −7 as −2 + −5 2x2 + (−2 −5) x + 5 Apply the distributive property. 2x2−2x−5x+5 Factor out the greatest common factor from each group. Group the first two terms and the last two terms. (2x2 − 2x) −5x +5 Factor out the greatest common factor (GCF) from each group. 2x (x − 1) −5(x −1) Factor the polynomial by factoring out the greatest common factor, x−1. (x−1) (2x−5)  Explanation For a polynomial of the form ax2 + bx + c, rewrite the middle term as a sum of two terms whose product is a ⋅ c = 3 ⋅ −5= −15 and whose sum is b = 2 Factor 2 out of 2x 3x2+2(x)−5 Rewrite 2 as −3 plus 5 3x2 +(−3 +5) x − 5 Apply the distributive property. 3x2 −3x + 5x − 5 Factor out the greatest common factor from each group. Tap for fewer steps... Group the first two terms and the last two terms. (3x2 − 3x) +5x − 5 Factor out the greatest common factor (GCF) from each group. 3x (x − 1) +5(x − 1) Factor the polynomial by factoring out the greatest common factor, x − 1 (x − 1) (3x + 5) |
| Home |
Accounting & Finance | Business |
Computer Science | General Studies | Math | Sciences |
Civics Exam |
Everything
Else |
Help & Support |
Join/Cancel |
Contact Us |
Login / Log Out |
