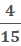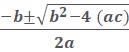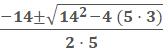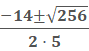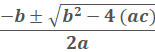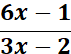College Algebra
(MAC-1105C) - Pre-Assessment Exam
Which number is irrational?


-5
Answer:
Explanation:
An irrational number
is a number that cannot be expressed as a fraction p/q for any integers p and
q.
Irrational numbers
have decimal expansions that neither terminate nor become periodic.
Every transcendental
number is irrational.
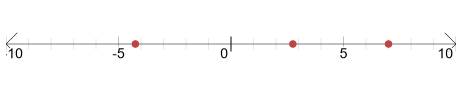
Which graph corresponds to the set of
real numbers:
{− 4.25, − π, 7, 2.75}?
The formula F = 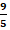 C
+ 32 is used to convert a Celsius temperature
C
+ 32 is used to convert a Celsius temperature
to its corresponding Fahrenheit
temperature.
What is the temperature in Fahrenheit
if the current temperature is −5°C?
23.0°F
Explanation:

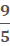 ·
· 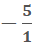 =
=  = -9
= -9
32 – 9 = 23
Driver A travels west from Boston at a
constant speed of 60 mph.
Driver B leaves three hours later from
Boston and follows Driver A at a constant speed of 72 mph.
How many hours would it take for
Driver B to catch up to Driver A?
15 hours
Explanation:
First, we write the formula:
60(3 + x) = 72x
Next, we simplify and solve for x.
180 + 60x = 72x
-60x -60x
That leaves us with
180 = 12x
Now we divide 180 by 12.
180 / 12 = 15
x = 15
What is the solution to x + 4 < 4x
- 5 expressed in interval notation?
(3, ∞)
Explanation:
Let's solve your inequality step-by-step.
x + 4 < 4x − 5
Subtract 4x from both sides. x + 4 − 4 x < 4 x − 5 − 4x
−3x + 4 < −5
Subtract 4 from both sides. −3x + 4 – 4 < −5 − 4
−3x < −9
Divide both sides by -3.
−3x −3 < −9 −3
x > 3
(3, ∞)
Which graph represents the following
equation?
y = 1/2x - 4
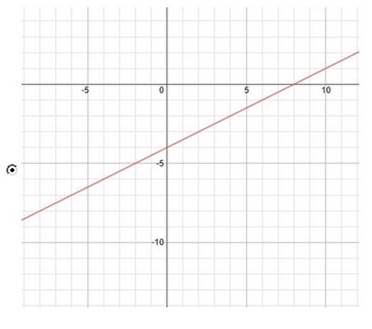
Explanation
Rewrite in slope-intercept form.
The slope-intercept form is y = mx +
b where m is the slope and b is the y-intercept.
y = mx + b
Reorder terms. y = 1/2x − 4
Use the slope-intercept form to find
the slope and y-intercept.
Slope: 1/2 y-intercept: (0, −4)
Any line can be graphed using two
points. Select two x values,
and plug them into the equation to
find the corresponding y values.
Reorder terms. y = 1/2x − 4
Create a table of the x and y values.
x y
0 4
2 -3
Graph the line using the slope and
the y-intercept, or the points.
Slope: 12 y-intercept: (0, −4)
x y
0 -4
2 -3
What is the slope of the line that
passes through the points (0, – 8) and (1/2, 4)?
24
Slope is equal to the change in y over the change in x or
rise over run.
m = 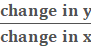
The change in x is equal to the difference in x-coordinates
(also called run), and the change in y
is equal to the difference in y-coordinates (also called
rise).
m = 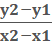 plug in the numbers m =
plug in the numbers m = 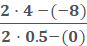
Now we apply the distributive property and solve for m.
(please note, 0.05 was converted from ½)
m = 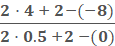 =
= 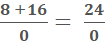
m = 24
College Algebra (MAC-2233) Lessons:
Pre-Assessment Exam
Final Exam (Proctored) Page
1 2 3
More Lessons 1 2
3 4 5 6 7 8 9 10 11 12 13 14
15 16 17 18 19 20 21 22
23 24 25
What is the equation of the line that
passes through the points (–3, 7) and (5, –1)?
y = −x + 4
Explanation:
Use y = mx + b
to calculate the equation
of the line,
where m
represents the slope and b
represents the y-intercept.
First, we find m like
so
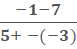 =
= 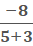 =
= 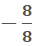 = -1, so m = -1
= -1, so m = -1
Now we find b like so
7 = (−1) ⋅ (−3) + b = 7 = 3 + b
Now, we want to move b alone, so we subtract 3 from 7
7 – 3 = b = 4 = b,
so b = 4
Now we plug in m and b in the
y = mx + b format
y = (-1)x + (4)
y = −x + 4
When the price for admission to a
sporting event was $100 per ticket, 50,000 people attended the event.
When the price increased to $108, the
attendance decreased to 45,000 people.
Which linear equation represents the
attendance (d) in terms of the admission price (p)?
d = –625p + 112,500
First, we need to place the values of this application in
ordered pairs.
(108, 45,000)
(100, 50,000)
Next, we use y2 – y1 / x2 – x1.
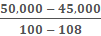 = -625
= -625
We will use y = mx + b to calculate the equation
of the line.
Next, we write the second equation and solve for y.
y − (45000) = −625 ⋅ (x − (108))
Simplify the equation and keep it in point-slope form.
y – 45000 = −625 ⋅ (x − 108)
Solve for y. Simplify
−625 ⋅ (x − 108)
y – 45000 = −625x + 67500
Move all terms not containing y to the right side of the
equation and we have the answer…
y = −625x + 112500
A stockbroker’s monthly salary is
$1,848 plus a sales commission of 5.2%
of the broker’s total sales for the
month.
Which equation represents the
stockbroker’s total monthly income (I)
based on monthly sales of x dollars?
I = 0.052x + 1,848
We will use y =
mx + b format however, we are given the equation.
All we do here is convert the commission 5.2 to a decimal.
So, 5.2 / 100 = 0.052. m = 0.052
We are given the value of b.
b = 1,848
So now we write the equation.
I = 0.052x + 1,848
The following four sets of points are
relations:
A = {(1,1), (5,2), (8,2), (9,3)}
B = {(1,1), (5,2), (5,3), (6,3)}
C = {(1,1), (1,2), (5,2), (6,3)}
D = {(2,1), (8,2), (8,3), (9,4)}
Which relation is a function?
Set A
A = {(1,1), (5,2), (8,2), (9,3)}
Explanation:
The relation which is a function is the relation set that
has all unique x’s.
A store is creating a 30 lb mixture of chocolates and nuts.
Chocolates cost $5.00
per pound, and nuts cost $2.50 per pound.
The store wants to make a mixture that
costs, on average, $3.00 per pound.
How many pounds of nuts are needed for
this mixture?
24 lb.
Explanation:
The two equations we need are:
x + y = 30
5x + 2.5y = 3x(x + y)
Now we solve this equation for y and then plug the value of
into the other equation.
We subtract x from both sides so y is alone.
x + y = 30 = y
= 30 – x
Now we plug in the value of y into the second equation.
5x + 2.5(30 – x) = 2(30)
Now
we
simplify.
5x
+ 75 – 2.5x = 60
Subtract 75 from both sides. 5x – 1.5x = -15
Simplify
the left
side.
2.5x
= -15
Divide 2.5 on both sides. -15
/ 2.5 = -6
x = -6
The weight of the chocolate = 6
Now we subtract 6 from the 30 lb. mixture.
30 – 6 = 24
A local credit union offers a
certificate of deposit (CD) that returns 2% interest and a money
market fund
that returns 3% interest. Over the next year, a
credit union customer wants to
earn $263.50 in interest on an investment of
$10,000 between a CD and a money market fund.
How much money will the customer need
to invest in the CD?
$3,650
This is the formula we need to write!
0.02x + .03(10,000 - x) = 263.50
Now we simplify.
.02x + 300 - .03x = 263.50
Simplify again by subtracting .02x - .03x = -0.1x
Now we subtract again (263.50 – 300)
-0.01x = -36.50
Now we divide -36.50 / -0.01
The answer is 3,650.
A restaurant manager pays servers
$8.50 per hour and bussers $5.50 per hour. The restaurant needs 8 people.
staffed on Saturday nights but can
only afford to pay a total of $59 per hour for staffing.
How many servers can be scheduled to
work on Saturday nights?
5
Explanation:
We can take some shortcuts with this one!!!
This is how it is done,
Let s = servers & Let b = bussers
These are the two equations we will deal with.
s + b = 8
8.5s + 5.5b = 59
Next, we multiple the first equation by -8.5
-8.5(s + b = 8) = -8.5s
+ -8.5b = -68
Now we factor and simplify the two equations.
(8.5s + 5.5b = 59) – (8.5s - 8.5b = -68)
8.5s – 8.50s = 0
5.5b – 8.5b = -3b
59 – 68 = -9
So, we are left with -3b
= -9
We solve for b by dividing both sides by -3
b (bussers) = 3
We need a total of 8 people (bussers and servers), so we
simply subtract…
8 – 3 =
5
severs = 5
A college student works two part-time
jobs.
The student works as a tutor for $40 per hour and at a coffeehouse for
$12 per hour. In one week the student works 22 hours and earns $404.
How many hours did the student work at
the coffeehouse that week?
17
Explanation:
This is the equation we need!
12t + 40(22 - t) = 404
We will solve for t.
12t + 880 - 40t = 404
Simplify the left 12t
– 40t = -28t
-28t + 880 = 404
We subtract 880 from both sides.
-28t – (880 = 880) = 404 – 808
We are left with -28t
= -476
Now we divide both sides by -28.
-28t / -28 = t
-476 / -28 = 17
t = 17
A dog breeder sells purebred puppies
for $1,200 each and adult dogs for $800 each.
The breeder sells 8 dogs at a dog show
for $8,400.
How many puppies did the breeder sell?
5
Explanation:
This is the equation we need to write and solve for p.
1200p + 800(8 - p) = 8400
1200p + 6400 – 800p = 8400
400p + 6400 = 8400
400p = 2000
p = 5
A child finds 30 nickels and dimes
between sofa cushions.
How many dimes did the child find if
the total value of the coins is $1.90?
8
Explanation:
This is the formula we need to write:
10d + 5(30 - d) = 190
Factor 5(30 – d)
10d + 150 – 5d = 190
Simplify
5d + 150 = 190
Subtract 190 - 150
5d = 40
Divide 40 / 5
d = 8
A bookstore has a clearance shelf with
$3 books and $5 books.
On Saturday, the bookstore sold 96 of the clearance books for a
total of $400.
How many of the $3 books were sold?
40
Explanation:
This is a problem that involves a slope.
Normally, we would need to solve for the y = mx + b format,
However, we are only
looking for one value, so we can take a shortcut!
You can look and match
my equation to the values from the problem.
It would be a lot
longer however I like to take as many shortcuts as I can.
I would suggest the
same for you. The equation makes perfect sense, so look it
over it carefully.
This is the equation
we need to solve. 3x + 5(96)
-5x = 400
We simplify, combine, and solve.
3x – 5x + 5(96) = 400 =
-2x + 480 = 400
Now we subtract 400 – 480 = -80
-2x = -80
Now we divide -80 / -2
x = 40
What is the result when (A3(A7)
is simplified?
A10
Explanation:
Simply add the exponents
because we add when we multiply a variable with exponents.
A3 + 7 = A10
What is the simplification of the
following expression?
(4x4 – 3x2 – 2x
– 1) – (5x3 + 2x2 + x - 4)
4x4 – 5x3 – 5x2
– 3x + 3
First, we need to factor the right side, since this is a
Simplification.
WE ARE NOT SUBTRACTING YET!
– (5x3 + 2x2 + x - 4) is the same as
– 1(5x3 + 2x2 + x - 4)
So, we need to multiply each number on the right side by -1
Now we can line the equations up and simplify.
When we multiply, we need to separate like terms.
4x4 comes first, and so on. I have lined them
up.
-5x3 – 2x2 – x + 4
4x4 – 3x2 – 2x –
1
= 4x4 – 5x3 -5x2 -3x + 3
What is the product of the following
expression?
–2x2(3x2 – x –
1)
–6x4 + 2x3 + 2x2
Explanation:
This is straight-forward.
We simply multiply the value of the left side by the values
in parenthesis.
Then we combine like terms and simplify.
–2x2 · 3x2 = 6x4
–2x2 · -x = 2x3
–2x2 · -1 = 2x2
Now we put everything in proper order of operation.
–6x4 + 2x3 + 2x2
College Algebra (MAC-2233) Lessons:
Pre-Assessment Exam
Final Exam (Proctored) Page
1 2 3
More Lessons 1 2
3 4 5 6 7 8 9 10 11 12 13 14
15 16 17 18 19 20 21 22
23 24 25
Factor: 10xy + 16x – 45y – 72.
(5y + 8) (2x – 9)
Explanation:
Factor out the greatest common factor from each group.
Group the first two terms and the last two terms.
(10xy + 16x) − 45y − 72
Factor out the greatest common factor (GCF) from each
group.
2x (5y + 8) −9(5y
+ 8)
Factor the polynomial by factoring out the greatest common
factor, 5y + 8.
(5y + 8) (2x − 9)
Factor the following trinomial: x2 – x – 6.
(x – 3) (x + 2)
Explanation:
First, we consider the form x2 + bx + c.
We then find a pair of integers whose product is c and
whose sum is b.
In this case, whose product is −6 and whose sum is −1.
−3, 2
Write the factored form using these integers.
(x − 3) (x + 2)
Factor the following trinomial:
3x2 + x − 10
(3x – 5) (x + 2)
Explanation:
For a polynomial of the form ax2 + bx + c, rewrite the middle term as sum of two
terms whose product
is a ⋅ c=3
−10 = −30
and whose sum is b = 1. Multiply by 1 3x2+1x−10
Rewrite
1 as −5 plus
6 3x2+(−5 + 6) x – 10
Apply the distributive property 3x2 − 5x + 6x – 10
Factor out the greatest common factor from each group.
Group the first two terms and the last two terms.
(3x2 − 5x) + 6x − 10
Factor out the greatest common factor (GCF) from each
group. x (3x − 5) + 2(3x − 5)
Factor the polynomial by factoring out the greatest common
factor, 3x−5.
(3x−5) (x+2)
What is the complete factorization of
the following trinomial?
6x 2 + 26x + 20
2 (x + 1) (3x + 10)
Explanation:
First, we factor out the GCF of 2 from 6x2+26x+20.
Factor out the GCF of 2 from each term in the polynomial.
Factor out the GCF of 2 from the expression 6x2.
2(3x2) + 26x + 20
Factor out the GCF of 2 from the expression 26x. 2(3x2) + 2(13x) + 20
Factor out the GCF of 2 from the expression 20. 2(3x2) + 2(13x) + 2(10)
Since all the terms share a common factor of 2, it can be
factored out of each term.
2(3x2+13x+10)
Factor by grouping. For a polynomial of the form ax2 +
bx + c rewrite the middle term as a sum of two terms whose product
is a ⋅ c = 3 ⋅ 10 = 30 and whose sum
is b = 13
2(3x2 + 3x + 10x + 10)
Factor out the greatest common factor from each group. Group the first two terms and the last two terms.
2((3x2 + 3x) + 10x + 10)
Factor out the greatest common factor (GCF) from each
group.
2(3x(x + 1) + 10(x + 1))
Factor the polynomial by factoring out the greatest common
factor, x + 1. 2((x + 1) (3x + 10))
What is the complete factorization of
the following binomial?
9x2 – 324
9(x – 6) (x + 6)
Explanation:
Factor out the GCF of 9 from 9x2−324.
Factor out
the GCF of 9 from each term in the polynomial.
Factor out the GCF of 9 from the expression 9x2 9(x2) − 324
Factor out the GCF of 9 from the expression −324. 9(x2) + 9(−36)
Since all the terms share a common factor of 9, it can be factored
out of each term.
9(x2 − 36) Rewrite
36 as 62 9(x2
− 62)
Since both terms are perfect squares, factor using the
difference of squares formula
a2 − b2 = (a + b) (a − b) where a = x
and b = 6
9(x+6) (x−6)
What are the solutions to the following
equation?
5x2 + 14x – 3 = 0
− 3, 1/5
This is a quadratic equation. We need to solve it.
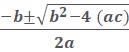 =
= 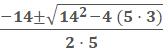
Explanation:
Next, we raise 14 to the power of 2. 
Next, we simplify the right side 196 – 4(5 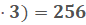
So, we are left with 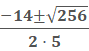
Next, we can rewrite  by squaring 256 and drop the radical.
by squaring 256 and drop the radical.
The square root of  = 162.
= 162.
Since it is a positive real number we can drop the radical.
We are left with 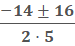 so we can simplify by dividing the top by 2.
so we can simplify by dividing the top by 2.
We are left with 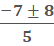
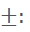 If we say
If we say 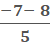 we will get
we will get  which equals -3
which equals -3
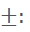 If we say
If we say 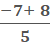 we will get
we will get 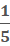 which equals
which equals
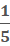
College Algebra (MAC-2233) Lessons:
Pre-Assessment Exam
Final Exam (Proctored) Page
1 2 3
More Lessons 1 2
3 4 5 6 7 8 9 10 11 12 13 14
15 16 17 18 19 20 21 22
23 24 25
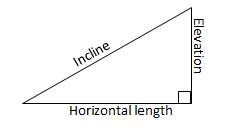
The incline of a roller coaster is 2
times as long as its elevation, and the horizontal length of the
roller coaster is 11m more than the
elevation. What is the length of the incline in meters?
30
Explanation:
This is the equation we need to
solve.
x2 + (x + 11)2
= (2x)2
Now we simplify.
(x + 11) (x + 11)
x2 + 11x + 11x + 121
x2 + x2 + 11x
+ 11x + 121 = 4x2
2x2 + 22x + 121 = 4x2
Now we subtract 4x2 from
both sides.
-2x2 + 22x + 121 = 0
We need to solve the quadratic
equation.
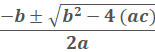
a = -2, b = 22, c = 121
The answer is x = 15.02627944.
We round that to 15.
The length of the incline is 2 times
the elevation,
So, we multiply 15(2) = 30
Two teams of interns are wrapping
donated gifts at a hospital. If the teams work alone, Team A can wrap
all of
the gifts in 7 hours, and Team B can wrap all of the gifts in 5 hours.
How many hours will it take the
interns to wrap all of the gifts if both teams work
together?
Round the answer to the nearest half
hour.
3.0
Explanation:
Simplest way to do this is like so and we do not need to
solve for x.
I see this around the internet, and it was never solved
correctly.
I did this in my head when I took the exam, however, I will
spell it out now!
This is how I did it!
IF team A had another team that could wrap gifts at the
same speed,
the two team A’ s would get it done in half the time! 7
hours / 2
IF team B had another team that could wrap gifts at the
same speed,
the two team B’ s would get it done in half the time! 5
hours / 2
So, this is how we wrap this problem up!
I put x in front but there is no need to because all we do
is add and simplify!
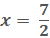 +
+ 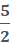 / 2
/ 2
Add the fractions and simplify.
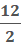 / 2
/ 2
So, we have 12 / 2 / 2.
12 / 2 = 6 and 6 / 2 = 3
What is the solution to the following
equation?
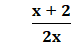 =
= 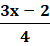
2 answers. 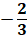 ,
2
,
2
Explanation:
Multiply the numerator of the first fraction by the
denominator of the second fraction.
Set this equal to the product of the denominator of the
first fraction
and the numerator of the second fraction.
(x + 2) ⋅ 4 = 2x (3x − 2)
Solve the equation for x - Since x is on the right side of
the equation,
switch the sides so it is on the left side of the equation.
2x (3x − 2) = (x + 2) ⋅ 4 Simplify 2x
(3x − 2)
Rewrite 0 + 0 +
2x (3x − 2) = (x + 2) ⋅ 4
Simplify by multiplying through 2 ⋅ 3x ⋅ x − 4x = (x + 2) ⋅ 4
Simplify each term. 6x2
− 4x = (x + 2) ⋅ 4 Simplify
(x + 2) ⋅ 4 6x2
− 4x = 4x + 8
Move all terms containing x to the left side of the
equation. 6x2 −8x
= 8
Subtract 8 from both sides of the equation. 6x2 − 8x – 8 = 0
Factor the left side of the equation. 2 (3x + 2) (x − 2) = 0
If any individual factor on the left side of the equation
is equal to 0,
the entire expression will be equal to 0. 3x + 2 = 0 x – 2 = 0
Set 3x + 2 equal to 0 and solve for x Set 3x + 2 equal to 0 3x + 2 = 0
Solve 3x + 2 = 0 for x.
x = 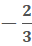
Set x − 2 equal to 0 and solve
for
x
x = 2
Simplify the following expression: 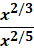
x4/15
Explanation:
Since we will be dividing variables with exponents in a
fraction,
We would simply multiply:
1x2/3 ⋅ 1x2/5
What is the value of x in the equation
3 +  =
10?
=
10?
24
Explanation:
3 + 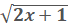 = 10
= 10
We subtract 3 from both sides 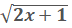 = 7
= 7
Now we square both sides and remove the radical
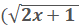 )2= 72, so
the radical drops out and we are left with:
)2= 72, so
the radical drops out and we are left with:
2x + 1 = 72 Now
we can simplify 72
We are left with 2x + 1 = 49
So, now we subtract 1 from both sides.
2x 1 – 1 = 49 – 1 =
2x = 48
Now we divide both sides by 2.
x = 24
What is the solution to the equation 15
- 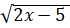 =
10?
=
10?
15
Explanation:
This is the same steps as above.
15 - 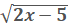 = 10
= 10
Subtract 15 from both sides. - 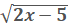 = -5
= -5
Square both sides (- 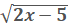 )2 = -52
)2 = -52
Drop the radical and simplify -52
*Note the negative (– 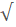 ) on the left gets
dropped as well)
) on the left gets
dropped as well)
So, we are left with 2x
- 5 = 25
Now we add 5 to both sides. 2x
= 30
Divide by 2
x = 15
What is the solution to the equation
(x + 2)2 = –12
−2 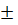 2i
2i
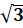
Explanation:
This is another quadratic problem. First, we simplify to
quadratic form.
First, we move all terms to the left side of the equation
and simplify.
Add 12 to both sides of the equation.
(x + 2)2 + 12 = 0
Simplify (x + 2)2 + 12
x2
+ 4x + 4 + 12 = 0
Add 4 and 12
We are left with:
x2 + 4x + 16 = 0
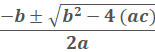
a = 1, b = 4, c = 16
What is the result when (P8(P7)
is simplified?
P15
Explanation:
Simply add the exponents
because we add when we multiply a variable with exponents.
P8 + 7 = P15
What is the solution to the equation
2x2 – 4x + 4 = 0?
x = 1 - 1i
x = 1 + 1i
Explanation:
You can do this the long way or use my quadratic equation
solver!
a = 2, b = -4, c = 4
http://www.coursesavior.com/quadsolver
What is the solution to the equation x2
+ 2x + 2 = 0?
x = 1 - 1i
x = 1 + 1i
Explanation:
You can do this the long way or use my quadratic equation
solver!
a = 1, b = 2, c = 2
http://www.coursesavior.com/quadsolver
A rectangle has an area of 256 cm2.
It has a width that is 48 cm shorter
than 4 times its length.
What is the rectangle's length?
16 cm2
Explanation:
A = LW
x (4x - 48) = 256
4x2 - 48x – 256 = 0
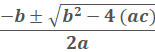
a = 4, b = -48, c = -256
You can do this the long way or use my quadratic equation
solver!
http://www.coursesavior.com/quadsolver
A rectangle has an area of 240 cm2.
It has a width that is 43 cm longer than its length.
What is the rectangle’s length?
5 cm
Explanation:
This is the formula…
x (x - 43) = 240
x2 - 43x = 240
x2- 43x – 240 = 0
We are left with a quadratic equation.
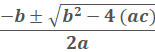
a = 1, b = -43, c = -240
You can do this the long way or use my quadratic equation
solver!
http://www.coursesavior.com/quadsolver
A rectangle has an area of 150 cm2.
It has a length that is 5 cm longer than its width.
What is the rectangle's length?
15 cm
Explanation:
150 = x2 - 5x
Factor x2 − 5x − 150 using the AC method.
Consider the form x2+bx+c.
We need to find a pair of integers whose product is c and
whose sum is b.
In this case, whose product is −150 and whose sum is −5
−15, 10
Write the factored form using these integers.
(x − 15) (x + 10) = 0
If any individual factor on the left side of the equation
is equal to 0,
the entire expression will be equal to 0.
x – 15 = 0
x + 10 = 0
Set x – 15 equals to 0 and solve for x
x = 15 Set
x+10 equal to 0 and solve for x
x = −10
The final solution is all the values that make (x − 15) (x
+ 10) = 0 true.
x = 15, −10
Which graph represents the function y = (x –
2)2 + 1?
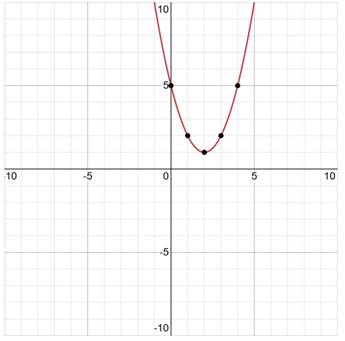
I solved a similar problem above!
Use the same steps to solve or use a graphing calculator.
Which graph represents the function y
= (x– 4) 2 + 5?

I solved a similar problem above!
Use the same steps to solve or use a graphing calculator.
Let f(x) = 3x – 2 and g(x)
= 6x – 1, What does 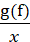 equal?
equal?
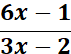
Explanation:
Simply place g(x) 6x – 1 over f(x) 3x – 2
The population of a town is 10,000
people.
The population is growing according to
the function P(t) = 10,000 2
where t is
the number of years from the present and P is the population.
What is the estimated population of
the town after 3 years?
10,644
Explanation:
This is the formula we need to use for
this problem.
P(t) = 10000(2)0.03t
We are given t = 3 so we plug it in
for the value of t.
10000(2)0.03(3)
Now we need to simplify a little to
solve with a calculator.
Enter it in the calculator like so:
10000 · 20.09
What is the solution to the equation log64x
= 2/3
16
Explanation:
642/3 = 16
An insurance annuity has an initial
principal of $3,500 and an annual interest rate of 7%.
The interest is compounded
continuously.
How many years will it take the
account to earn $475 in interest?
Round to the nearest tenth.
1.8 years
Explanation:
First, convert R as a percent to r
as a decimal
r = R / 100
r = 7 / 100
r = 0.07 per year,
Then, solve the equation for t
t = ln (A / P) / r
t = ln (3,975.00 / 3,500.00) / 0.07
t = 1.818025 years
A savings account has a beginning principal of $12,500 and an annual interest rate of 1.75%.
The interest is compounded continuously.
How many years will it take the
account to earn $1,125 in interest?
Round to the nearest whole number.
5 years
Explanation:
First, we convert R as a percent to
r as a decimal.
r = R / 100
r = 1.75 / 100
r = 0.0175 per year
Then, solve the equation for t
t = ln (A / P) / r
t = ln (13,625.00 / 12,500.00) / 0.0175
t = 4.92444 years
We round to the nearest whole number
= 5
What is the value of x in the
exponential equation 45 – 9x =
 x – 2?
x – 2?
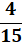
Explanation:
Apply the product rule to 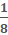 45 – 9x
=
45 – 9x
= 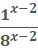
One to any power is one 45 – 9x
= 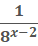
Move 8x – 2 to the numerator using the negative
exponent rule (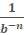 )
)
45 – 9x = 8-(x –
2)
Create equivalent expressions in
the equation that all have equal bases.
22(5-9x) = 23(-(x
– 2))
Since the bases are the same,
then two expressions are only
equal if the exponents are also equal.
2(5 − 9x) = 3(−(x − 2))
Solve for x Simplify
2(5 − 9x) 10−18x = 3(−(x − 2))
Simplify 3(−(x−2)) 10
− 18x = −3x + 6
Move all terms containing x to the left side of the
equation. 10 − 15x = 6
Move all terms not containing x to the right side of the
equation. −15x = −4
Divide each term in −15x = −4 by −15 and simplify.
x =