Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel

---

---

Compute the derivative of the function f(x) =

                   Answer:     2x csc x – (x² – 1) cot x csc x

Explanation:

 (x² – 1) csc(x)
Use the product rule:          (x² – 1) ( (csc(x)) + csc(x) ( (x² – 1))
Differentiate the sum term by term:   csc(x)  (x² – 1) + csc(x))
The derivative of csc(x) is -cot(x) csc(x)         csc(x)  (x²) +  (x² – 1) -cot(x) csc(x)
The derivative of -1 is zero.          csc(x)  (x²) +  (x² – 1) -cot(x) csc(x)
The derivative of x² is 2x.             2x csc x – (x² – 1) cot x csc x

A 4 ft. long wire could be cut into two pieces.
One piece is bent into a circle and the other into a square.
What would the length of the side of the square need to be if the sum of the areas is a maximum?

                   Answer: 0 ft. ü

Solution:

Write the equation and find the SECOND devirative

 = 4x + 4

Find the derivative of 4x + 4 = 4
Find the derivative of 4 (which is the second derivative of 4x + 4)
The derivative of 4  = 0        Or     f’(x) of 4x + 4 = 4

f’’(x) of 4x + 4 = 0

f(x) = (x² + 3x)² find f” (-1)
                   Answer: -6 ft. ü
Explanation:
f” means to find the derivative of the equation TWICE and plug in the value.
Factor (x² + 3x)² = x⁴+ 6x³+ 9x²
Find the derivative of x⁴+ 6x³+ 9x² =     4x³ + 18x² + 18x
Find the derivative.              12x² + 36x + 18
Plug in the value of f (-1)     12(-1)² + 36(-1) + 18
Simplify     12 - 36 + 18
30 – 36 = -6 Calculate f’(x) if f(x) = x⁴ + 2x
                   Answer: 4x³ + 2 ü
Explanation:
n^{n -1}
4 · x^{4 – 1} = 4x³
2x^{1 – 1} = 2
4x³ + 2 What is the derivative of the function f(x) = ?
 

Explanation: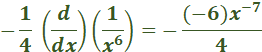

 

Simplify   =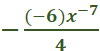  
  A physical fitness room consists of a rectangular region with a semicircle at each end. If the perimeter of the room is
to be a 200 ft running track, what is the radius of the semicircle that will make the rectangular region a maximum.


Explanation:
 = 0
 

200 = 4x
200 / 4 = 50
 ft

  What is the derivative of     f(x) = 2^x
 
2^x ln 2

 [2^x]
 
Explanation:
the Exponential Rule states that  [a^x] =   a^x ln (a)

Since, in this case, a = 2 we simply rewrite
a^x ln (a)
(2)^x ln (2)   or      2^x ln 2
When x is used as an exponent, the derivatives are as follows:
Derivative
2^x =   2^x ln (2)
3^x =   3^x ln (3)
4^x =   4^x ln (4)               And so on…

What is the derivative of the function f(x) = ln (x + ln x).
 
 
Explanation:
f’(x) =
f’(x) =
 =

Now we rewrite so that the equation matches the answer.
Find the derivative of f(x) = e^{x^2}
 
                   Answer: 
 
We use the chain rule for this.
 [e^u]  [x²] = e^u  [x²] =
_ex²  [x²]

Now we use the Power Rule nx^{n – 1} and n = 2
_ex²(2x)

Now we rewrite to match the answer.
_2xex² A man 6 feet tall is walking toward a building at the rate of 5 ft /sec.  If there is a light on the ground 50 ft from the
building, how fast is the man’s shadow on  the building growing shorter when he is 30 ft from the building?
                   Answer:  ft / sec
 
Explanation:
First, we write the equation.
 =

We need to have “h” on the left all alone.           h(t) =  =
 
Since we are looking for the height, we are supposed to use 2 forms for “x” with this problem,  because we are
trying to track movement. Which would be x and x^’.  However, we (I) can use x and y and x and y are as follows:

x = 30                         y = 5

Now we rewrite the last step we worked on so we can plug in the values of x & y.

Now we plug in the values x = 30 & y = -5    
 =    =  =  

---

Evaluate the following as true or false.
Given f(x) = 2 , a good choice for x when evaluating f (12.1)
by the method of linear approximation x = 12.

                   Answer:     True

Suppose a particle’s position is given by f(t) = t⁴,  where t is measured in seconds and f(t) is given in centimeters.
What is the velocity of the particle when t = 3?
 
                   Answer:     v = 108 cm / sec
 
Explanation:
Find the derivative of t⁴ and plug in the value t = 3
First the derivative of t⁴ =         4 (t)^{4 – 1} = 4t³
Now we plug in the value of t = 3
4(3³)
4 x 3³ = 4 x 27 = 108 What is the derivative of the function f(x) =
                   Answer:
 
Explanation:


Find the derivative of the function     f(x) = (5x⁴ - 2x² + 7x + 4) (2x² - 5).
 
                   Answer:     (20x³ – 4x + 7) (2x² - 5) + 4x (5x⁴ - 2x² + 7x + 4)
 
Explanation:
Derivative of 5x⁴ - 2x² + 7x + 4 = 20x³ – 4x + 7
Now we find the derivative of 2x² – 5 = 4x
Then we multiply 4x by 5x⁴ - 2x² + 7x + 4) =
4x (5x⁴ - 2x² + 7x + 4) and put the equation back together.
(20x³ – 4x + 7) (2x² - 5) + 4x (5x⁴ - 2x² + 7x + 4)
  What is the equation of the line tangent to the curve,
xy + 1 + e = e^-xy at the point (1, -1)?
 
                   Answer:     y = x – 2
 
Explanation:
We find the derivative of xy + 1 + e = e^-xy
We plug in the values x = 1 and solve for y          xy + 1 + e = e^-xy
e^-xy = x-y (positive because -1 x -1 = 1 / and -1 x 1 = -1)
Now we move x to right the side to plug in the
value for x (which is 1) and y (which is -1) and solve for y.

-(-1) y = -(1) =     1y = -1

Now we subtract 1 from both sides.

y = -1 + -1 =         y = -2 What is the derivative of f(x) = e^2x
 
                   Answer: 2e^2x
 
Explanation:
We have covered this. We simply multiply the equation by 2.  Since the exponent is x, and we are dealing with e,
we do not need to change it to “ln” this time.
2(e^2x) = 2e^2x

What is the derivative of y = xe^x + x²
 
                   Answer:     e^x + xe^x + 2x
 
Explanation:

What is the derivative of the function:
f(x) =
 
                   Answer: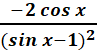   
 
Explanation:


 

---

 
What is the derivative of f(x) = e^x+1 – 1
 
                   Answer:     e^{x + 1}
 
Explanation: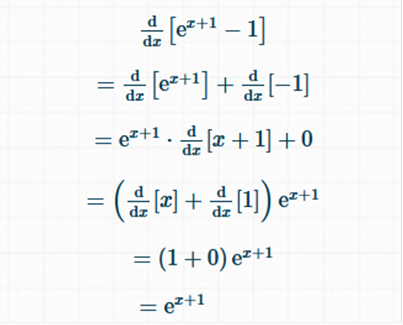

 
A man 6 feet tall walks at a rate of 5 ft/sec away from a light that is 15 feet above the ground.
When he is 10 feet from the base of the light, at what rate is the length of his shadow changing.
 
                   Answer:  ft / sec
 
 
Explanation: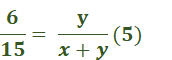

15y = 6x + 6y
 =   


What is the slope of the line tangent to the curve:
x³ + y³ = 2x² y² at the point (1, 1)
 
                   Answer: -1
 
First, we find the derivative of x³ + y³ = 2x² y²
Then we plug in the values.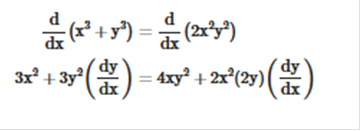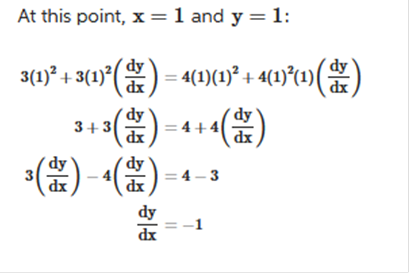


A rectangular field is to be fenced off on three sides with the fourth side being the bank of a river.
If the cost of the fence is $8 per foot for the two ends and $12 per foot for the side parallel to the river,
what are the dimensions of the largest rectangle that can be enclosed with $3840 worth of fence?
                   Answer:     120 ft by 160 ft
 
Explanation: This is crazy, but here it is!
3840 = 8x + 8x + 12y                3840 = 16x + 12y            12y = 3840 – 16x
Divide by 12 = y =  =
Reduce
y = 320 -                 a = xy
y = x (320 - )         y = 320x - ²

Now we find the derivative and solve for zero.
Derivative of 320x - ² =         320 -  = 0
Add
  = 320
Divide both sides by

x = 320 x 3 / 8                 x = 960 / 8                 x = 120
Now we plug in the value of x into the following equation.
3840 = 8x + 8x + 12y
Since we have already been down this road, we will set up the equation
instead of factoring and simplifying all over again.
 of factoring 16x + 12y so we simply multiply 120
y =  
x = 120
so
y = 120 ( =
160
Answer = 120 ft by 160 ft.


What is the derivative of f(x) = ln 2x?

                   Answer: 1/x
 
Explanation:

Compute the derivative of the function     f(x) = tan (2x + 1)
 
                   Answer:     2 sec² (2x + 1)
 
Explanation:
Given xy = y³, find dy/dx by implicit differentiation.
                   Answer:

Explanation:
Compute the derivative of the function f(x) = 
                  
Explanation:
Use the linear approximation method to estimate the value of ln (2.7²) in terms of e.


Explanation:

e = 2.718281828459045

We multiply 2.718281828459045 x 2

round to 1 decimal place, and divide by e.


 
A manufacturer wants to make open tin boxes from pieces of tin with dimensions 8 in. by 15 in.
by cutting equal squares from the four corners and turning up the sides. Find the side of the square
cutout that gives the box the largest possible volume.
                  

Explanation:
The base has a length of 15 - 2x inches and a width of 8 - 2x inches.
The box has a height of x inches.
Volume of the box is volume =
(15 - 2x) (8 - 2x)x = 4x³ - 46x² + 120x
We find the derivative and set it equal to 0
12x² - 92x + 120 = 0
x = [-b ± √(b² - 4ac)]/2a
so, x = [92 ± √(92² - 4 · 12 · 120)]/(2 * 12)
x = 5/3 or x = 6
Since x cannot be 6 inches, the answer is x = 5/3 inches
  Use implicit differentiation to find an equation of the line tangent to the curve
x² + y² = 10 at the point (3, 1).
                   Answer:     y = -3x + 10

Explanation:
Find the derivative of x² + y² = 10 = 2x + 2y
Set to equal zero = 2x + 2y = 0
differentiate on both sides (subtract 2 – 2 and divide x by y)
The fraction is now negative.
2x + 2y = -x + y =

Now plug values into the equation of tangent (3,1)
y – 1 = m (x – 3)
Solve for y when m = -3
y – 1 = -3 (x – 3)            y = -3x + 9 + 1          y = -3x + 10
  What is the derivative of the function f(x) = -6x²   - 6x
 
                   Answer:     -12x +  - 6
 
Explanation:
Find the derivative like so.
-6x² = 2 · -6x^{2 – 1} = -12x
  · -2²⁺¹ =  
-6x · 1^{1 – 1} = -6
Now put the equation back together
-12x +
  Given x² - y² = 1, find dy/dx by implicit differentiation
                  
 
Explanation:
x² – y² = 1
differentiate both sides of the equation.
The derivative of -y² = -2y
the derivative of x² = 2x.
So, we are left with -2y + 2x = 1
(since 1 is a constant, with respect to x, the derivative of 1 is 0).
-2y + 2x = 0
-2 + 2 = 0
Now we solve y + x = 0.
Divide x by y.    
What is the derivative of the function f(x) = 3x⁹?

                   Answer: 27x⁸

Explanation:
Find the derivative like so
3x⁹ · n^-1
9 · 3x^{9 – 1}
27x⁸

What is the derivative of the function f(x) = sin² x + tan (x² + 1)

                   Answer: 2 sin x cos x + 2 x sec² (x² + 1) ü

Explanation:
The derivative of sin x is cos x.
The derivative of tan is sec².
First, we will simplify.
sin² x + tan (x² + 1) =
sin² x + tan x + tan x + 1
The derivative of sin² x = 2 sin x cos x
The derivative of tan x + tan x + 1 = 2 x sec² (x² + 1)
Now we put the equation back together.
2 x sec² (x² + 1) + 2 x sec² (x² + 1)

A car and a truck leave the same intersection, the truck heading north at 60 mph and the car heading
west at 55 mph. At what rate is the distance between the car and the truck changing when the car and
the truck are 30 miles and 40 miles from the intersection, respectively?

                   Answer: 81 mph

Explanation:
The easiest way to do this is like so.
We set up the equation.
Since the car and the truck are 30 miles and 40 miles from the intersection
We square the distance, which will be negative, and add them together.
That is the only information we are not given.
30² + 40² = 2,500
Now we find the square root of 2,500.
√2,500 = 50 (Since the distance has not been reached yet, the pythagorean theorem will be negative).
We are given the rest of the information so all we need to do is set up the equation.
(50 will now be negative).
-50 = (30 · -55) + (40 · -60)
-50 = -1,650 + -2,400
-50 = -4,050
Now we divide both sides by -50
Answer = 81 What is the derivative of f(x) = 2^x

                   Answer: 2^x ln 2

Explanation:
When x is used as an exponent, the derivatives are as follows:
Derivative
2^x =   2^x ln (2)
3^x =   3^x ln (3)
4^x =   4^x ln (4)
And so on…
*With or without the parentheses

---