Need A Tutor?    |   Need Homework Help?                                                                             Help and Support     | Join or Cancel

---

---

A function is defined as f (x) = x ²− 5x + 3. Evaluate f (0)
 
                                      Answer: f (0) = 3
Explanation:
Replace the variable x with 0 in the expression:
f (0)= (0)² - 5 · 0 + 3
Simplify the result: f(0)= 0 + 0 + 3
Simplify again: f(0) = 3

---

a. Understand and manipulate nested fractions.
b. Understand graphs and data plots.
c. Find the volumes of oddly shaped objects.
d. Solve systems of linear equations.

A particular rectangle has a length of 3 feet and a width of 2 feet.
What is the area of the described rectangle?
 
                                      Answer: 6 square feet
Explanation:
Steps: 3 · 2 = 6 ft² 
Determine the Limit, if it exists:

                             Answer: ü
 
Explanation:
Find the derivative.
Derivative of x² – 5x + 6 =           2 · 1x^{2 – 1} – 1x · 5x^{1 – 1} + 6 =           2x - 5
Derivative of x² – 4 = 2x


Move the term ½ outside of the limit because it is constant with respect to x:
½ ·

Plug in the value of 2 (lim à 2), evaluate the limit of 5, which is constant as x approaches 2,
and drop the x from the denominator.
½ ·
1 · (2 · 2) + (-1 · 5) / 2 · 2 = 4 + -5 / 4 =
  Consider the function y = x² − 3x + 2.
At what value of x is the slope of the tangent line equal to 5?
 
                             Answer:      4
 
Find the Derivative of y = x² - 3x + 2     =        2x – 3
n^n-1
x² = 2 · x^{2 – 1} = 2x
-3x = 1 · 3x^{1 – 1} = 3x
2 · 0 = 0
Derivative = 2x – 3
Then set value to 5.
2x – 3 = 5
Add 3 to both sides = 2x = 8
Divide both sides by 2.
x = 4
  Calculus (MAT-251)     Graded Exam  1     2.1     2.2     2.3     3.1     3.2     4.1    4.2       Midterm   1    2     Final Exam  1   2            

Determine the Limit, if it exists.
 

 
                                                 Answer:  0 ü
 
Explanation

Take the limit of each term.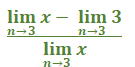

Evaluate the limit by plugging in 3 for x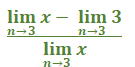

Evaluate the limit of 3 which is constant as x approaches 3.

Evaluate the limit by plugging in 3 for x
 =  = 0
  Let f’(x) = 3x² + 4x define the instantaneous rate of change in (ft/min) of a car moving along the x-axis.
What is the instantaneous rate of change at time 1 min?
 
                                      Answer:      7 ft/min
 
          Explanation:
          Plug 1 into the equation 3x² + 4x
          f (1)  =  3 (1)² = 4 (1)  =     7 ft/min If x changes from x = 1 to x = 2 along the curve y = x ², which if the following is equal to Δy ?
 
                                      Answer:  3

Explanation:
y = 2² (4)
– y = 1² (1)
4 – 1 = 3 
 
If f(x) =  and f(g(x)) = x, then what is g(x)?
 

 
Explanation:
              
2.                    
3.  = x
4.       
5.  = x


For which values of k will the line y = x + k meet the parabola of the equation
y = −x ² + 4x − 8 in two distinct points
 
                             Answer:      k < -23/4
Explanation
x + k = -x²+ + 4(x) – 8
x² + 3x – 8 – k = 0 (quadratic equation has two solutions)
Solve the quadratic equation
Answer:      k < -23/4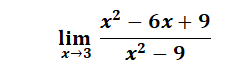
Determine, if it exists

 
                                      Answer:  0 ü
Solution:
Plug in the value of x = 3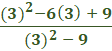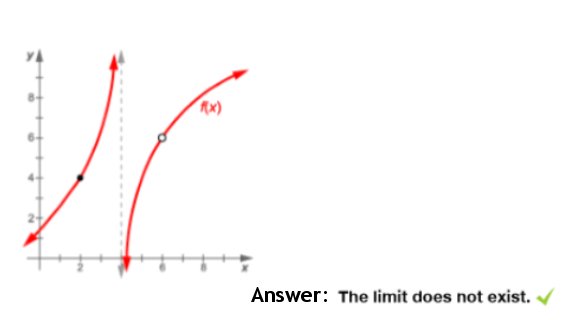
 =  =  = 0
  What is the limit of the function in the graph at x\ = 4?
What is the average rate of change of the function y = 4x³ − 2 between x = 2 and x = 4?
 
                             Answer:      112
 
Solution:
Rewrite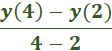

Plug in the value of y.
  

Simplify
 =  =  = 112
  For what value(s) of x does the function in the graph not have a limit?

                    Answer:      4 and 6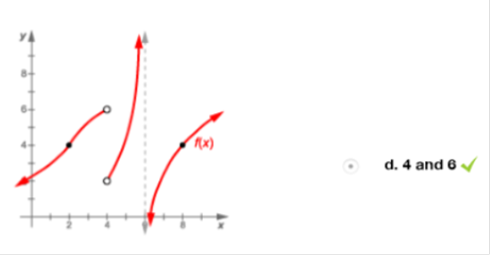

Solution:
A body is thrown upward so that its height h at the end of t seconds is h = 160t − 16t² ft.
Which of the following is its maximum height?
 
                             Answer:  400
 
Find the derivative of 160t – 16t² and solve for zero.
160 – 32t = 0
-32t = -160
t = 5
Then plug in the value of t = 5.
160(5) – 16(5)²
800 – 16(25)
800 – 400 = 400
   
Consider the variables p, v, t, and T related by the equations:  pv = 4T, T = 100 − t, and v = 10 − t.
 
                             Answer:  4

Explanation:
P =

Plug in the values.
 -
 
Solve
 =  = 4


What is the average rate of change of the function,
y = 2x² + 3 between ^x1 = x and x = ^x2
 
                             Answer:  2 (x₂ + x₁)
 
Explanation:
Average rate = [y · (^x2) – y · (^x1)] ÷ (^x2 - ^x1)
= [2 · x₂² - 2 · x₁²] ÷ (x₂ – x₁)
= 2 (x₂ - x₁) (x₂ + x₁) ÷ (x₂ - x₁)
= 2(x₂ + x₁)
  What is the average rate of change of the function,
y = 2x² + 3 between x = 2 and x = 4
 
                             Answer:  12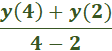
 


Plug in the value of y.
  
Solve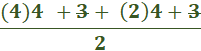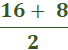


 = 12


Evaluate the derivative of the function: f (x) = (x − 2)^-1
 


Solution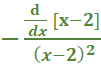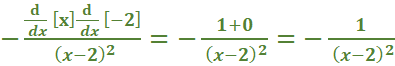
 =
 
What is the limit of the function in the graph at     x = 4

                   Answer:  12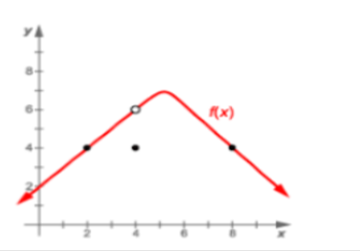

Apply the definition of the derivative to differentiate the function f(x) = x
 
                   Answer:      1
 
Solution:
x can be written as 1x¹
n^n-1
1(1x^{1 – 1}) = 1


What is the limit of the function in the graph at x = 4
 
            Answer:      2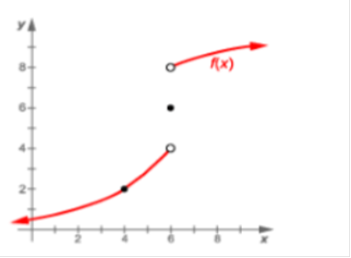

At 2:00 p.m. a car is traveling at 22 mph. Four minutes later the car is traveling at 32 mph.
Was the car ever moving at 30 mph over this interval? Why or why not?
 
        Answer:     Yes, the car was moving at 30 mph at least once over the interval.

Explanation:
The reason is that the car had to accelerate 30 mph to reach 32 mph.

 
What is the slope of the secant line of the function,
y = −2x² + 3x − 1     between     x = ^x1 and x = ^x2
 
                   Answer:      -2x₁ – 2x₂ + 3

Explanation: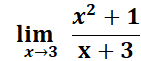
Determine, if it exists,
                        
 
                        Answer:


Explanation:
Plug in the value x = 3.
  =            =  

Consider the function y = x² − 2x + 1.
What is the slope of the tangent line at x = 2
                        Answer:     2

Solution:
y = x² − 2x + 1
 = 2x - 2
x = 2
2(2) – 2 = 2

---